B树

最新推荐文章于 2024-09-04 23:28:18 发布

凌琅Zxin

最新推荐文章于 2024-09-04 23:28:18 发布

阅读量275

点赞数 1

分类专栏：算法

本文链接：https://blog.csdn.net/Zhxin606a/article/details/88673989

版权

算法专栏收录该内容

36 篇文章 1 订阅

订阅专栏

https://www.cnblogs.com/guohai-stronger/p/9225057.html

https://www.cnblogs.com/lwhkdash/p/5313877.html

http://www.cnblogs.com/yangecnu/p/Introduce-B-Tree-and-B-Plus-Tree.html

B-树，即为B树。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是一种一种树。而事实上是，B-tree就是指的B树。特此说明。

B树（B-tree）是一种树状数据结构，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。

B 树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树。与红黑树很相似，但在降低磁盘I/0操作方面要更好一些。

B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。
B树与红黑树一样，一棵含n个结点的B树的高度也为O(lgn），但可能比一棵红黑树的高度小许多，应为它的分支因子比较大。
所以，B树可以在O(logn)时间内，实现各种如插入(insert)，删除(delete)等动态集合操作。

下图一棵关键字为英语中辅音字母的B树

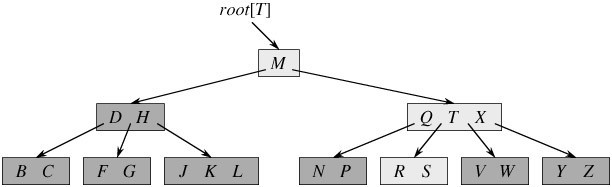
一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女（比如含关键字D、H，那么它的孩子肯定是在D之前的，处于D和H之间的，位于H之后的）

所有的叶结点都处于相同的深度。

B 树又叫平衡多路查找树。一棵m阶的B 树 (m叉树)的特性如下：

树中每个结点最多含有m个孩子（m>=2）；
除根结点和叶子节点外，其它每个节点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
若根结点不是叶子节点，则至少有2个孩子（特殊情况：没有孩子的根节点，即根结点为叶子节点，整棵树只有一个根节点）；
所有叶子节点都出现在同一层，叶子节点不包含任何关键字信息(可以看做是外部节点或查询失败的节点，实际上这些节点不存在，指向这些节点的指针都为null)；（读者反馈@冷岳：这里有错，叶子节点只是没有孩子和指向孩子的指针，这些节点也存在，也有元素。@JULY：其实，关键是把什么当做叶子节点，因为如红黑树中，每一个NULL指针即当做叶子节点，只是没画出来而已）。
每个非终端节点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
       a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。
       b)   Pi为指向子树根的节点，且指针P(i-1)指向子树种所有节点的关键字均小于Ki，但都大于K(i-1)。
       c)   关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。

针对上面第5点，再阐述下：B树中每一个节点能包含的关键字（如之前上面的D H和Q T X）数有一个上界和下界。这个下界可以用一个称作B树的最小度数（算法导论中文版上译作度数，最小度数即内节点中节点最小孩子数目）t（t>=2）表示。

每个非根的节点必须至少含有t-1个关键字。每个非根的内节点至少有t个子女。如果树是非空的，则根节点至少包含一个关键字；
每个节点可包含之多2t-1个关键字。所以一个内节点至多可有2t个子女。如果一个节点恰好有2t-1个关键字，我们就说这个节点是满的（而稍后介绍的B*树作为B树的一种常用变形，B*树中要求每个内节点至少为2/3满，而不是像这里的B树所要求的至少半满）；
当关键字数t=2（t=2的意思是，tmin=2，t可以>=2）时的B树是最简单的（有很多人会因此误认为B树就是二叉查找树，但二叉查找树就是二叉查找树，B树就是B树，B树的真正最准确的定义为：一棵含有t（t>=2）个关键字的平衡多路查找树）。每个内节点可能因此而含有2个、3个或4个子女，亦即一棵2-3-4树，然而在实际中，通常采用大得多的t值。

B树中的每个节点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

1.1 举例

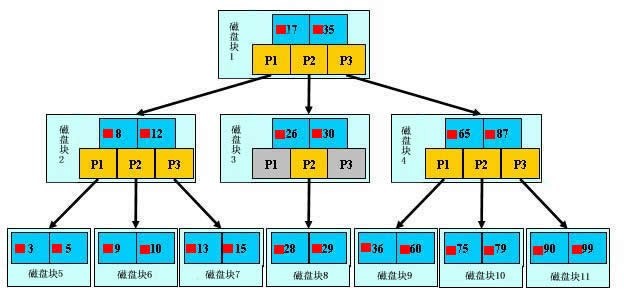
上面的图中比如根结点，其中17比表示一个磁盘文件的文件名；小红方块表示这个17文件内容在硬盘中的存储位置；p1表示指向17左子树的指针。

其结构可以简单定义为：

typedef struct {
       int  file_num;  //文件数
 
       char * file_name[max_file_num];   //文件名(key)

       BTNode * BTptr[max_file_num+1];  //指向子节点的指针
    
       FILE_HARD_ADDR offset[max_file_num];   //文件在硬盘中的存储位置

}BTNode;

假如每个盘块可以正好存放一个B树的结点（正好存放2个文件名）。那么一个BTNODE结点就代表一个盘块，而子树指针就是存放另外一个盘块的地址。

下面，咱们来模拟下查找文件29的过程：