摘要: 本文以黄土高原区域为研究样区探讨了基于 DEM 和 GIS 的流域水文信息提取过程中阈值确定的有关问题,运用python数学建模中的最小二乘拟合模型和 ArcGIS中的 Hydrology水文分析工具,进行了不确定性研究。后续研究结果表明:1 阈值对河网信息提取具有较大的影响,当重分类时将阈值以下的区域设置为汇流区时,阈值越小,河网越稀疏。当阈值设置为9500时提取的河网实际水系基本符合。2.Hydrology水文分析工具中的支流个数和河流长度是明显的线性关系。水流累积量的阈值和河流长度有明显的相关性。
关键词:DEM;GIS;水文分析; 黄土高原;最小二乘拟合模型;数学建模
1 引言
DEM,是对地球表面地形地貌的一种离散的数学表达,即数字高程模型。DEM的应用十分广泛,因其包含地表的地形地貌和水文信息,可以用于地形特征提取和水文分析等方面。其中水文分析是常见的DEM应用类型。基于DEM的地表水文分析的主要内容是利用水文分析工具提取地表水流径流模型的水流方向、汇流累积量、水流长度、河流网络,以及对研究区的流域进行分割等[1]。通过对这些基本水文因子的提取和基本水文分析,可以在DEM表面之上再现水流的流动过程,最终完成水文分析过程。
在利用ArcGIS完成的水文分析实验中,基于地表径流漫流模型的水文提取具有一定的不确定性。例如,在沟谷网络提取时,设置不同的阈值也得到不同的沟谷网络。本实验主要探讨在不同阈值下,沟谷网络提取结果的不确定性。以不同阈值提取汇水网络,并将其转换为矢量线的格式,来对比其空间位置差异以及各项统计值,如支流数目、沟谷总长度等的变化。
学者们对流域水文特征的研究,大多是对流域水文信息提取方法的研究,其中水流累积量中阈值确定是研究的重点,本文应用 Arc GIS 中的 Hydrology 水文分析工具,以黄土高原为研究样区,基于研究区 DEM 数据提取流域水文信息,通过水流累积量中阈值的突变点确定河网提取阈值,运用数理方法对阈值进行判定,减少以往根据河网对比判定阈值的误差,最终提取得到与实际流域最吻合的水系。

图1 研究流程图
2 实验样区和数据来源
本研究选择中国黄土高原作为实验样区。黄土高原位于中国内陆西北部, 黄河中游地区, 地跨100°54′ —114°33′E与33°43′ —41°16′N之间, 总面积约63万平方公里,是我国黄土分布最广泛的典型地区。它是世界上黄土覆盖面积最厚、最完整、土壤侵蚀现象最严重的地区。研究区以黄土塬,黄土梁,黄土峁等典型黄土地貌为主,以石质山地,风沙丘陵,河流冲击平原地貌为辅,形成了黄土高原独特而丰富的地貌景观[2]。黄土高原区域水系以黄河为骨干,发源于黄土高原的河流较多,约有200条,较大的有洮河、祖厉河、清水河、黄甫川、窟野河、无定河、北洛河、渭河、沁河、汾河等。河川径流不包括黄河干流年径流总量185亿立方米。

图 2 研究区概况
本文的DEM数据来自于地理空间数据云的 GDEMV2-30m 分辨率数字高程数据;通过 ArcGIS 的“按掩膜提取”功能得到黄土高原的数字高程数据。

图 3 黄土高原的30m分辨率 DEM数据
3 水文分析
水文是地形的基本框架,在地貌学、水文学等研究中具有重要的地位,也是与地表水文情况有关的许多领域如区域规划、农业、林业等的基础数据。自从DEM出现以来,水文分析就成为DEM应用中一个非常重要的内容。ArcGIS中,基于DEM的汇水网络提取主要是基于地表径流漫流模型[3],其步骤如图3,主要是;(1)洼地填充;(2)水流方向计算;(3)水流汇流累积量计算; (4)水流长度计算;(5)河水网络提取等。

图 4 ArcGIS水文分析工具流域生成流程图
3.1 无洼地 DEM 生成
洼地是水流方向不合理的地方由于DEM影像数据会因为分辨率等原因导致地面高程高低起伏,并且有洼地可能被识别成为伪河谷,在后续水流方向计算时,得不到正确的水流方向。因此,可以利用ArcGIS中水文分析里Fill工具对DEM数据设置合理的填充阈进行洼地的填充得到无洼地的DEM。

图5填挖前后的洼地剖面图
通过上述洼地填充过程, DEM中所有栅格点的高程值均大于或等于最低出水口点的高程值, 这样就创建了一个具有“水文学意义”的DEM, 从而保证了从DEM数据中提取的流域自然水系是连续的[3]。

图6无洼地DEM图
3.2 水流方向提取
水流方向是指经过每一个栅格时水流的指向,在ArcGIS中水文分析里Flow Direction工具, 输入原始的DEM数据, 通过D8算法得到水流方向。

图7水流方向码
D8算法假设每个单元格的水流只有8种可能的流向并用最陡坡度法来确定水流的方向。为了方便地表示水流方向,一般规定一个网格的水流方向用一个特征码表示。有效的水流方向定义为东、东南、南、西南、西、西北和北、东北,并分别依次用值为2的次幂的8个有效特征码表示。

图8水流方向计算结果图
3.3 汇流累积量计算
模拟地表径流的模型中,通过流向的数据计算出汇流累积量。分析地表径流可知,每一个栅格中,其汇流累积量的数值代表着上游水流方向汇聚后流向该栅格的数量,汇流累积的数值越大,则该位置越容易形成地表径流[4]。在ArcGIS处理过程为在水文分析的流量工具中输入流向分析结果,运行即可得到汇流累计量结果。

图9基于水流方向计算汇流累计量的计算过程
汇流累积量是基于水流方向数据计算而来的。对每一个栅格来说, 其汇流累积量的大小代表着其上游有多少个栅格的水流方向最终汇流经过该栅格, 汇流累积的数值越大, 该区域越易形成地表径流。

图10水流累积量计算结果图
3.4 不同阈值的河网提取
汇流累积量的计算是河网提取的基础,当汇流量达到一定值后就会产生地表水流,所有汇流量大于临界值的栅格就是潜在的水流路径,由此构成的网络就是河网。阈值的确定是河网提取的关键环节,它直接决定生成的数字河网的密度和形态[5]。
利用 ArcGIS中水文分析逐步提取相关水文信息,重分类水流累积量时,将大于阈值的DEM数据设置为1值,其余为NoData,从1000作为河流提取的阈值开始,间隔1000提取一次,设置从1000到10000一共10个汇流累积量阈值生成栅格河网。通过图 11- 图 20 对比分析可以得出个结论:1.不同的阈值对提取的河网密度有较大影响。2.当阈值由 1000 增至 10000 时,随着阈值增大,提取的流域河网越来越密集;各级河网的条数和长度都随阈值的增大而呈现不同程度的增加。



4 结果与分析
根据国家地球系统科学数据中心提供的黄土高原地区水系图与不同阈值下的河网密度对比发现在阈值设置为9000到10000时较为吻合,将阈值设置为9500得到提取的水系可以发现与真实河网基本相似。

图21黄土高原地区水系图与阈值为9500时河流密度图对比
左图源于国家地球系统科学数据中心
为了详细讨论实际汇流累积量阈值的设定,本文利用利用 ArcGIS 中统计工具得到汇流累积量阈值与河流长度以及支流个数的关系表如下:
表 1 汇流累积量阈值与河流长度以及支流个数的关系
| 阈值 | 河流长度(km) | 支流个数(个) |
| 1000 | 1955.029 | 18 |
| 2000 | 2495.145 | 23 |
| 3000 | 2821.664 | 26 |
| 4000 | 3143.549 | 29 |
| 5000 | 3466.533 | 32 |
| 6000 | 4669.017 | 43 |
| 7000 | 5089.582 | 47 |
| 8000 | 6184.012 | 57 |
| 9000 | 10859.374 | 100 |
| 10000 | 23465.617 | 216 |
4.1相关性检验
首先对数据进行相关性检验,保证研究的有效性与科学性。本研究采用皮尔逊相关系数(Pearson correlation coefficient)作为相关性检验的工具,其相关系数计算公式如下:




图22阈值与河流长度以及支流个数的相关性分析结果图
结果显示,阈值与河流长度之间的相关系数为0.78,表明两者之间存在中等程度的正相关关系。阈值与支流个数之间的相关系数也为0.78,同样反映出中等程度的正相关关系。此外,河流长度与支流个数之间的相关系数接近1.00,这表明两者之间存在极强的正相关关系。
经此相关性检验,可以认定本文中三类数据存在继续分析价值,故对此数据集进行进一步分析。
4.2 汇流累积量阈值对河网特征的影响
由于将阈值与河流长度,阈值与支流个数之间都有较强的相关关系,因此可以对实验数据绘制趋势来观察数据之间的一个大致走向,判断黄土高原研究区河流长度以及支流个数与阈值关系的方程类型。

图 23阈值与河流长度以及支流个数关系图
观察之后可以发现两幅图有较强的相似度,因此可以推断阈值和河流长度有线性关系,而河流长度和支流个数有倍数关系。下面将汇流累积量重分类的阈值作为横轴,分别将流域长度和支流个数作为纵轴绘制散点图,并使用线性函数、二次函数、三次函数、幂函数、指数五种函数进行基于最小二乘法的拟合分析对推测进行验证。
4.2.1 最小二乘法
最小二乘法,又称最小平方法,是一种通过最小化误差平方和寻找数据的最佳函数匹配,并使求得数据与实际数据之间误差平方和最小的数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合[7]。
样本之间具有明显的正相关性,因此对样本做出有函数关系的假设,对于汇流累积量阈值与河流长度以及支流个数样本,本研究中拟合了如下四个假设模型:
表 2 五个假设模型的拟合方程
| 拟合方程 | 公式 |
| Poly1 | y = p1 x + p2 |
| Poly2 | y = p1x 2 + p2x + p3 |
| Poly3 | y = p1x 3 + p2 x 2 + p3 x + p4 |
| Power2 | y = axb + c |
| Exp1 | y = aebx |
最小二乘法会根据误差平方和SSE和拟合优度R-square 两个重要评价指标的相对大小选择合适的描述变量关系的模型。
SSE表示计算拟合数据和原始数据对应点的误差平方和,反应随机误差对因变量y的影响。
4.2.2 最小二乘模型的建立与求解
根据最小二乘拟合的思想,基于python进行数学建模,选用五种不同种类的拟合方式, 通过比较SSE和 R-square的数值大小选取拟合黄土高原研究区河流长度与阈值效果最优的模型。

图 24阈值与河流长度以及支流个数关系图
使用python对于每个函数求解SSE和R-square的结果得到表3。其中指数分析的拟合效果较差,系统没有给出拟合曲线和误差平方和,认为该曲线不能满足其精度的最低要求,并不适合用于阈值和河流长度的拟合关系,但是由表3可知误差的平方和最小是1.424695,拟合优度最大是0.962792,分别在两条不同的曲线中,但是综合分析,给出最优的表达式:
![]()
表 3 阈值与河网密度的拟合结果

下面对河流长度和支流个数进行线性拟合发现两者有较强的线性关系:
![]()
查阅ArcGIS的帮助发现两者是基于同一个算法算出来的结果。

图 25河流长度和支流个数关系图
4.3 河网提取评价
根据图 24 可知阈值与河流长度以及支流个数关系可以分为几个阶段,下面使用突变点检测将其进行分类。
4.3.1 突变点检测
突变点检测隔离了数据序列中的突然变化。Ruptures算法提供了二进制分割、动态编程和Pelt等方法。
关键算法和公式如下:
二进制分割:通过递归划分数据来检测变化点。

动态编程:确保变化点检测中的全局优化。
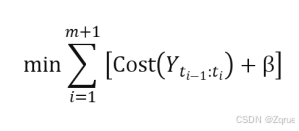
Pelt:有效地找到最优的变化点集。
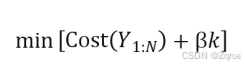
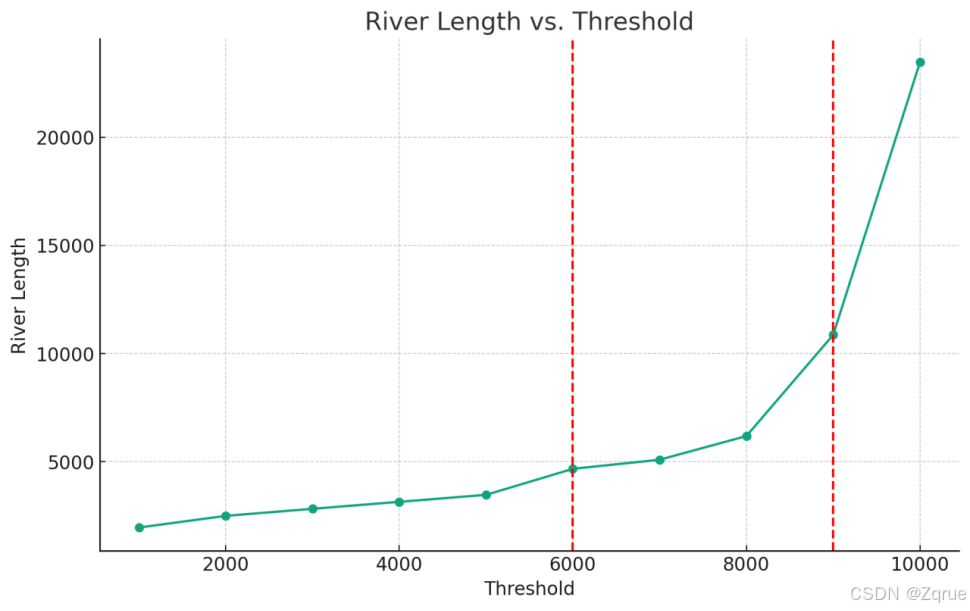
图 26突变点检测结果图
由图可得到计算出来的2个突变点可以将两者的变化趋势分为3部分:平缓部分、缓慢增加、快速上升。第一个由平缓部分到缓慢增加的突变点是细小沟道上河网链消失的阈值分界点。第二个由逐渐增加到快速上升认为是坡面上河网链消失的阈值分界点;[5]第二个突变点之后的9500阈值,是能较好提取水系的阈值点,在第二突变点之前,水的汇集与流动受到河网的约束,第二突变点之后会有较多伪河道的出现,因此将9500设置为黄土高原流域区的水流累积量阈值是较好的选择。
5 结论与讨论
运用 ArcGIS的水文分析工具对DEM 数据提取流域水文特征信息的方法具有速度快、方便的特点,能广泛应用于流域水文分析,为水资源管理提供技术支持。但不同分辨率的 DEM 数据可能会对提取的河网结果产生影响,并造成与实际情况的差异。本文由于DEM分辨率的有限性,难以做到对流域面积,流域的河网密度进行提取是可以进行优化的地方。
阈值的设定对流域河网的提取具有较大的影响。重分类水流累积量时,将大于阈值的DEM数据设置为1值,其余为NoData,可以得到结论:不同的阈值,提取的河 网不同,阈值越小,河网越稀疏,阈值越大,河网越稀疏,当阈值达到9500时,提取的河网与实际河网基本一致。
本文先对ArcGIS得到的阈值,河流长度以及支流数目进行了基于Python的数学建模分析,首先确定了三者的相关性,其次建立了五个线性函数用最小二乘法进行拟合,最后做突变点分析找到对阈值影响最大的突变点,详细探讨了阈值对于河流长度以及支流数目的关系,有助于提高提取结果的客观性和精确性。
6.参考文献
[1]杨雪峰.利用DEM数据划分流域探析[J].水土保持应用技术,2022(04):55-57.
[2]林偲蔚,陈楠,刘奇祺等.基于DEM小流域复杂网络的黄土高原地貌自动识别研究[J].地球信息科学学报,2022,24(04):657-672.
[3]安祺,杨霏,陈丹等.基于Hydrology的山区1:1万DEM水系提取研究[J].重庆工商大学学报(自然科学版),2012,29(11):87-92.
[4]张鹏举,孟宪萌,周宏,等.不同集水面积阈值确定方法在典型黄土侵蚀地貌区的适用性分析[J].水电能源科学,2019 ,37(8):26-29.
[5] 李照会,郭良,刘荣华,等.基于DEM数字河网提取时集水面积阈值与河源密度关系的研究[J].地球信息科学学报,2018,20(9):1244-1251.
[6]唐杰,程麒铭,陈垚.基于ArcGIS-Matlab的流域集水面积阈值确定方法[J].水电能源科学,2021,39(07):46-48+153.
[7]Wang Y ,Li H ,Liao L .DEM Construction Method for Slopes Using Three-Dimensional Point Cloud Data Based on Moving Least Square Theory [J].Journal of Surveying Engineering,2020,146(3):04020013-04020013.
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








