本文首先对LDA的原理和算法进行了介绍,其次比较了LDA和PCA的异同,最后使用sklearn以绘图的方式比较了LDA和PCA。
目录
一、LDA的简介
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的线性学习方法,在二分类问题上因为最早由Fisher提出,因此也被称为“Fisher判别分析”。LDA的基本思想是“最大化类间距离,最小化类内距离”。
对于线性判别分析LDA,有两点需要注意:
- LDA是一种有监督学习算法,在二分类问题上最早被提出。
- 这里所说的LDA代表“线性判别分析(Linear Discriminant Analysis)”,而不是NLP领域中的LDA(latent Dirichlet allocation).
二、LDA的原理
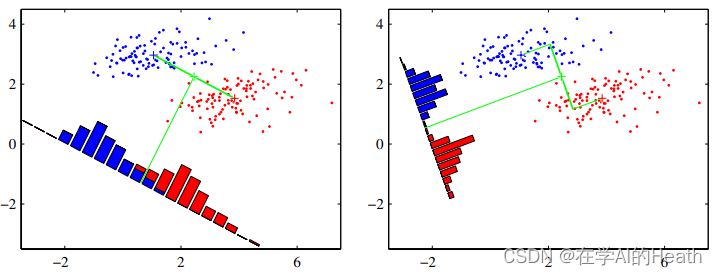
LDA原本是为了分类服务的,如左上图所示。我们希望两类之间投影距离尽可能大,也就是说两类之间的均值尽可能大。容易发现,当直线方向与(
)方向一致的时候,该距离达到最大值。但是投影到下方黑线之后,原本可以被线性划分的两类样本,经过投影后有了一定程度的重叠,这显然不是我们想要的结果。
而如右上图所示,虽然两类的中心在投影之后距离有所减少,但是投影后可区分度更高了,投影后的样本点似乎在每一类的分布中更集中了。也就是说,每类内部的方差比左图中更小。这就引出了LDA的中心思想:最大化类间距离和最小化类内距离。
对于LDA的讲解,我会分为二分类的情况和多分类的情况,首先看二分类的情况:
2.1 二分类的LDA原理
一、类内距离
我们有两类样本,两类的均值分别为
,其中
则两类样本中心在直线上的投影为
,
因此两类样本各自的类内距离可表示为
二、类间距离
如果每一类数据在投影后分布越密集,也就是说投影后的方差越小,那么也就是等价于类间距离越大,使用分别表示两类投影后的方差,则:
三、目标函数及其求解
如果要类内距离尽可能大,类间距离尽可能小,那么我们接引出了需要最大化的目标:
等价于:
我们定义类间散度矩阵
类内散度矩阵
则有:
我们注意到上式中的分子和分母都是关于的二次项,因此式(1)的解与
的长度无关,只与其方向有关。令
,则式(1)等价于:
使用拉格朗日乘子法,定义拉格朗日函数为:
对求偏导可得
由于,所以
令上式等于=,即可得,也就是
若令,则有
四、得出结论
由于最终要求解的不关心其大小,只关心其方向,所以其大小可以任意取值。又因为
大小固定,所以
的大小只受
的大小影响,因此可以调整
的大小使得
。总之,若不考虑
的长度,那么就可以得到
。换句话说,对于二分类问题,我们只需要求样本的均值和类内方差,就可以马上得到最佳投影方向
。
考虑到数值解的稳定性,在实践中常常对进行奇异值分解,即
,再由逆变换,得到
。
2.2 多分类的LDA原理
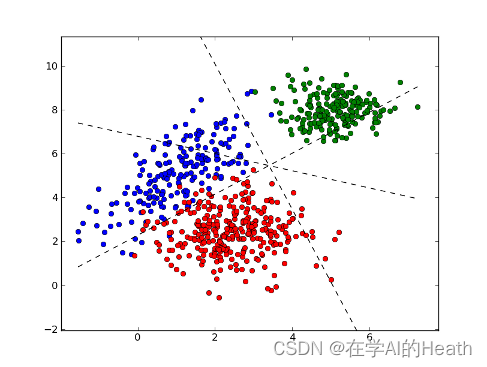
假设我们有N个类别,并需要最终将特征降到d维。因此,我们要找到一个d维的投影超平面,使得投影后的样本点满足L最大化类间距离和最小化类内距离。
当有多个类别时,2.1中的类间散度矩阵就不适用了。因此我们可定义一个新的矩阵表示全局整体的散度,称为全局散度矩阵:
若,即全局散度=类内散度+类间散度,那么类内散度可表述为:
其中是第
个类别中心的样本个数,
是总类别个数。
我们最大化类间散度是加上优化的是每个类别中心经过投影后离全局中心投影足够远,因此可将最大化目标定为:
引入拉格朗日乘子,最大化对应以下广义特征值求解问题:
右乘得
求解最佳投影平面即求解
矩阵前
大特征值对应的特征向量组成的矩阵,这就将原始特征空间投影到新空间中。
三、LDA和PCA的区别与联系
3.1 从数学推导的角度
根据第二章的推导,我们就得到了和PCA非常类似的LDA求解方法:
(1)计算数据集中每个类别的样本均值向量
,以及总体均值向量
。
(2)计算类内散度矩阵
,全局散度矩阵
,并得到类间散度矩阵
、
(3)对矩阵
进行特征值分解,将特征值从大到小排列。
(4)取前
大的特征值对应的特征向量
,通过以下映射将
维样本映射到
维。
从PCA和LDA两种降维方法的求解过程看,它们确实有很大的相似性,但是在原理上却有所区别:
首先从目标出发,PCA选择的是投影后数据方差最大的方向。由于无监督,因此PCA假设方差越大,信息量越多,用主成分来表示原始数据可以去除冗余的维度,达到降维。
而LDA选择的是投影后类内方差小、类间方差大的方向。其用到了类别标签信息,为了找到数据中具有判别性的维度,使得原始数据在这些方向上投影后,不同类别尽可能分开。
3.2 从应用的角度
在语音识别中,我们想从一段音频中提取出人的语音信号,这时可以使用PCA先进行降维,过滤掉一些固定频率(方差较小)的背景噪声。但如果我们的需求是从这段音频中区分出声音属于哪个人,那么我们应该使用LDA对数据进行降维,使每个人的语音信号具有区分性。
另外,在人脸识别领域中,PCA和LDA都会被频繁使用。基于PCA的人脸识别方法也称为特征脸(Eigenface)方法,该方法将人脸图像按行展开形成一个高维向量,对多个人脸特征的协方差矩阵做特征值分解,其中较大特征值对应的特征向量具有与人脸相似的形状,故称为特征脸。Eigenface for Recognition一文中将人脸用7个特征脸表示,于是可以把原始65536维的图像特征瞬间降到7维,人脸识别在降维后的空间上进行。然而由于其利用PCA进行降维,一般情况下保留的是最佳描述特征(主成分),而非分类特征。如果我们想要达到更好的人脸识别效果,应该用LDA方法对数据集进行降维,使得不同人脸在投影后的特征具有一定区分性。

从应用的角度,我们可以掌握一个基本的原则——对无监督的任务使用PCA进行降维,对有监督的则应用LDA。
四、LDA和PCA在Iris数据集上的体现
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)
lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
# Percentage of variance explained for each components
print(
"PCA explained variance ratio (first two components): %s"
% str(pca.explained_variance_ratio_)
)
print(
"LDA explained variance ratio (first two components): %s"
% str(lda.explained_variance_ratio_)
)
plt.figure()
colors = ["navy", "turquoise", "darkorange"]
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(
X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=0.8, lw=lw, label=target_name
)
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("PCA of IRIS dataset")
plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(
X_r2[y == i, 0], X_r2[y == i, 1], alpha=0.8, color=color, label=target_name
)
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("LDA of IRIS dataset")
plt.show()运行结果如下图所示:
PCA explained variance ratio (first two components): [0.92461872 0.05306648]
LDA explained variance ratio (first two components): [0.9912126 0.0087874]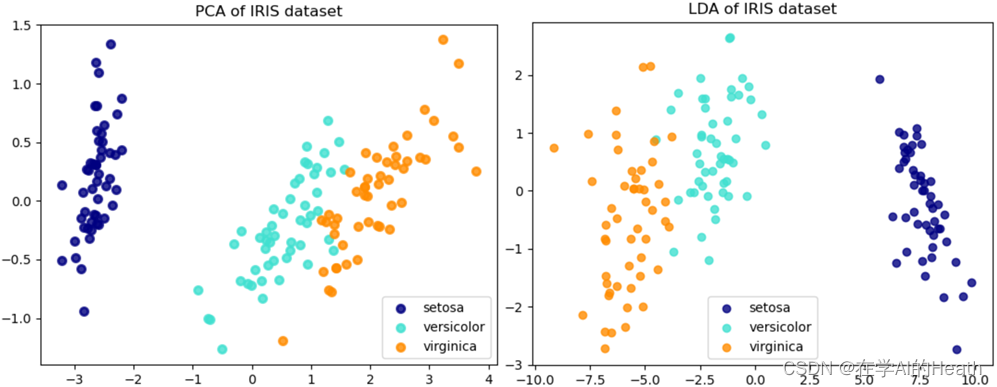
总的来讲,LDA相对于PCA在有标签的数据降维中表现得更好。
























 2373
2373











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








