有趣~2023 ICPC 亚洲区域赛南京站构造题 —— H.谜题（附带源码）

Zz_0913

已于 2024-01-10 22:45:05 修改

阅读量526

点赞数 13

分类专栏：构造专题基础算法文章标签：算法 c++ c语言深度优先推荐算法数学建模

于 2024-01-10 22:03:47 首次发布

本文链接：https://blog.csdn.net/Zz_0913/article/details/135512073

版权

基础算法同时被 2 个专栏收录

3 篇文章 0 订阅

订阅专栏

构造专题

1 篇文章 0 订阅

订阅专栏

打过Codeforces的同学们都知道，CF上有一类非常锻炼思维的难题就是构造题，几乎每场div中都会有这样子的题目，构造题有很多种，比如：

构造数列的👇：

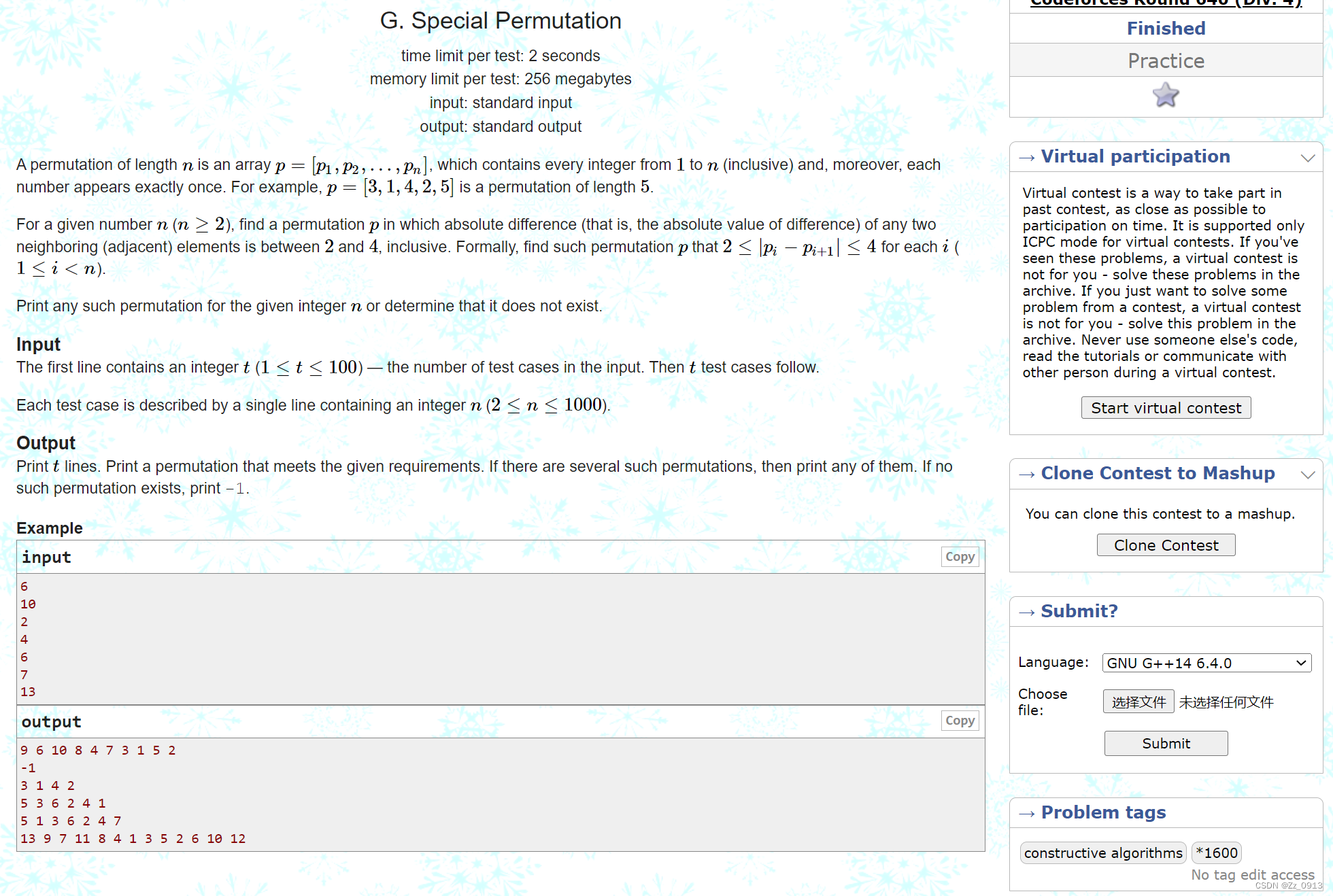
构造矩阵的👇：

构造一颗树的👇：

等等，这些都是非常直观的构造题，因为它们的构造对象非常的具象，然后还有一些比较抽象有难度的构造题，比如构造路线，游戏方案，博弈路径这些。然后在我们的ICPC-ACM等竞赛中，必定会出现一道构造题，往往是属于13道题目中的夺冠题，包括这次2023 ICPC 南京站中的H.谜题：

题意是什么呢？我来简化一下：

在一个 n × n 的网格内不重叠地放入尽可能多的问号拼图（QM 拼图），QM 拼图可以旋转和翻面，输出最多能放置的 QM 拼图数量以及对应的方案。

这道题目也是非常明显的构造矩阵的题目，也有点类似矩阵填数题，一眼望去怎么有点像二维01背包or状态压缩Dp呢🤔（像国王问题，炮兵阵地，射击这样的问题）？那就不属于构造题了呀~,不过这样一想，南京站剩下就没有构造了，并且我们通过几个例子发现它并没有二维连通性，因此是不能通过状压解决的（随便想想，这个问号都可以随便转，怎么说也是二维0k背包呀😄），所以对于这道题，我们还是用解构造题的思维来看叭——>先从构造方法，构造特殊情况入手，然后推往普遍情况，发现普遍构造方法o(￣▽￣)ｄ：

首先我们画出这些拼图能变出的所有样式👇：

单个 QM 拼图的形状过于不规则，我们可以将两块 QM 拼图以不同的方式拼起来，构成如下三种基本块（可旋转和翻转）👇：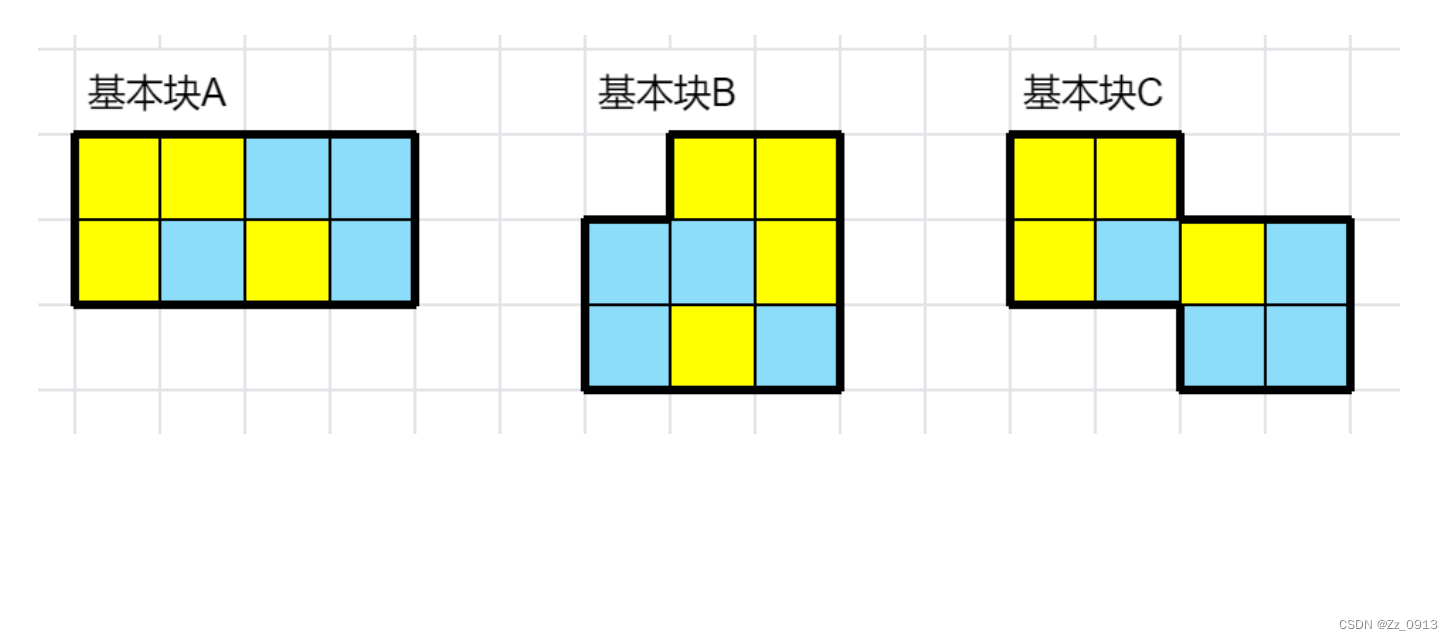

然后我们从特殊情况入手分析：

假如n为偶数：

1.对于 n = 4k 的情况，只需从上至下，从左至右放置 2k × k个 2 × 4 的基本块 A 即可恰好填满。

2.对于 n = 4k + 2 的情况，首先不可能做到用 QM 拼图恰好填满，这是因为将网格黑白交替染色，黑白方格各有2 × (2k + 1) × (2k + 1) 个，QM 拼图需要 (2k + 1) × (2k + 1)个，每个占据 3 黑 1 白或者 1 黑 3 白，最后占据的黑色格子数奇偶性不符。

3.接下来说明有 4 个格子空余的构造方案：先用 (2k + 1) × k个 2 × 4 的基本块 A 填满左侧 (4k + 2) × 4k 的区域，再用 k × 1 个 4 × 2 的基本块 A 填满右上角 4k × 2 的区域，最后空出右下角 2 × 2 的区域。

假如n为奇数：

下面是 n = 1,3,5,7时的构造方案，并由暴力搜索证明该方案最优（n = 5, 7会空余 5个）。

对于n为奇数且 n ≥ 9，均有构造方案使得只有1个空余格子（不同于 n = 5, 7 会空余 5 个）

n = 9 的构造如下👇：

然后我们通过4k+1的情况，推出4k+3和4k+5的情况：

总体来说，对于 n ≤ 8 或者 n 为偶数的情况，采取直接构造；对于 n ≥ 8 且 n 为奇数的情况，用上述两种递归构造最终归约到 n = 9 的情况。时间复杂度为 O(n^2),OK,我们直接上代码👇（在线输出）🤔：

#include<bits/stdc++.h>
using namespace std;
int N,idx;
int A[2005][2005];
#define Temp template<typename T>
Temp inline void read(T &x)//快速读入，这里感觉没什么必要😄，才10^3量级
{
    x = 0;
	T w = 1,ch = getchar();
    while(! isdigit(ch) && ch != '-')
	    ch = getchar();
    if(ch == '-')
	    w = -1,ch = getchar();
    while(isdigit(ch))
	    x = (x << 3) + (x << 1) + (ch ^ '0'),ch = getchar();
    x = x * w;
}
void add(int x,int y)//放置函数
{
	assert(0 <= x && x < N);
	assert(0 <= y && y < N);
	assert(A[x][y] == 0);
	assert(idx >= 1);
	A[x][y] = idx;
}
void place(int x,int y,int t)//x,y表示放置位置，t表示QM图标的样式，为放置函数；
{
	idx++;
	if(t == 0)
	{
		add(x,y);
		add(x,y + 1);
		add(x + 1,y + 1);
		add(x + 2,y);
	}
	else if(t == 1)
	{
		add(x,y);
		add(x + 1,y + 1);
		add(x,y + 2);
		add(x + 1,y + 2);
	}
	else if(t == 2)
	{
		add(x,y + 1);
		add(x + 1,y);
		add(x + 2,y);
		add(x + 2,y + 1);
	}
	else if(t == 3)
	{
		add(x,y);
		add(x,y + 1);
		add(x + 1,y);
		add(x + 1,y + 2);
	}
	else if(t == 4)
	{
		add(x,y);
		add(x,y + 1);
		add(x + 1,y);
		add(x + 2,y + 1);
	}
	else if(t == 5)
	{
		add(x,y + 1);
		add(x,y + 2);
		add(x + 1,y);
		add(x + 1,y + 2);
	}
	else if(t == 6)
	{
		add(x,y);
		add(x + 1,y + 1);
		add(x + 2,y);
		add(x + 2,y + 1);
	}
	else if(t == 7)
	{
		add(x,y);
		add(x,y + 2);
		add(x + 1,y);
		add(x + 1,y + 1);
	}
	else assert(false);
}
void solve()//核心处理部分
{
	if(N % 4 == 0)//4的倍数特殊情况
	{
		for(int i = 0;i < N;i = i + 4)
		{
			for(int j = 0;j < N;j = j + 2)
			{
				place(i,j,0);
				place(i + 1,j,6);
			}
		}
	}
	else if(N % 4 == 2)//4k+2情况的放置
	{
		N = N - 2;
		solve();//递归~
		N = N + 2;
		for(int i = 0;i < N - 2;i = i + 4)
		{
			place(i,N - 2,0);
			place(i + 1,N - 2,6);
			place(N - 2,i,3);
			place(N - 2,i + 1,5);
		}//逐个放置
	}
	else if(N % 4 == 3)//4k+3的情况处理
	{
		N -= 2;
		solve();
		N += 2;
		for(int i = 0;i < N - 3;i = i + 4)
		{
			place(i,N - 2,0);
			place(i + 1,N - 2,6);
			place(N - 2,i,3);
			place(N - 2,i + 1,5);
		}
		place(N - 3,N - 2,0);
		place(N - 2,N - 3,3);
	}
	else
	{
		assert(N % 4 == 1);//4k+1的情况处理
		if(N == 1);
		else if(N == 5)//特殊情况5
		{
			place(0,0,0);
			place(1,0,6);
			place(0,2,7);
			place(0,3,6);
			place(3,2,1);
		}
		else if(N == 9)//特殊情况9
		{
			place(7,4,3);place(7,1,1);place(7,0,7);
			place(6,7,6);place(6,5,0);place(5,7,0);
			place(5,0,1);place(4,3,6);place(4,0,0);
			place(3,5,6);place(3,2,4);place(2,7,6);
			place(2,6,7);place(2,4,4);place(1,0,6);
			place(0,6,1);place(0,5,7);place(0,2,1);
			place(0,2,2);place(0,0,0);
		}
		else if(N == 13)//特殊情况17
		{
			place(0,0,0);place(1,0,6);place(0,2,0);
			place(1,2,6);place(11,6,1);place(11,5,7);
			place(11,0,1);place(10,11,6);place(10,9,6);
			place(10,3,6);place(10,0,0);place(9,11,0);
			place(9,9,0);place(9,6,3);place(9,2,4);
			place(8,7,0);place(8,4,6);place(8,0,7);
			place(7,3,4);place(6,11,6);place(6,9,6);
			place(6,8,7);place(6,5,1);place(6,5,2);
			place(6,0,4);place(5,11,0);place(5,1,6);
			place(4,6,1);place(4,3,1);place(4,3,2);
			place(3,9,6);place(3,6,0);place(2,11,6);
			place(2,10,7);place(2,8,4);place(1,4,6);
			place(0,10,1);place(0,9,7);place(0,6,1);
			place(0,6,2);place(0,4,0);place(4,0,3);
		}
		else
		{
			assert(N >= 17);//对于大于17的情况，或者大于9的情况，都有一定使其空一个格子的解
			N -= 8;
			solve();
			N += 8;
			place(9 + N - 11,8 + N - 11,3);place(9 + N - 11,5 + N - 11,1);
			place(9 + N - 11,4 + N - 11,7);place(9 + N - 11,1 + N - 11,1);
			place(9 + N - 11,0 + N - 11,7);place(8 + N - 11,9 + N - 11,0);
			place(7 + N - 11,6 + N - 11,1);place(7 + N - 11,3 + N - 11,3);
			place(7 + N - 11,0 + N - 11,1);place(6 + N - 11,6 + N - 11,0);
			place(6 + N - 11,4 + N - 11,0);place(6 + N - 11,0 + N - 11,0);
			place(5 + N - 11,9 + N - 11,6);place(5 + N - 11,8 + N - 11,7);
			place(5 + N - 11,2 + N - 11,7);place(4 + N - 11,6 + N - 11,7);
			place(4 + N - 11,3 + N - 11,3);place(3 + N - 11,8 + N - 11,1);
			place(3 + N - 11,5 + N - 11,3);place(3 + N - 11,0 + N - 11,1);
			place(3 + N - 11,0 + N - 11,2);place(2 + N - 11,7 + N - 11,3);
			place(1 + N - 11,3 + N - 11,6);place(0 + N - 11,9 + N - 11,6);
			place(0 + N - 11,8 + N - 11,7);place(0 + N - 11,5 + N - 11,1);
			place(0 + N - 11,5 + N - 11,2);place(0 + N-  11,3 + N - 11,0);
			for(int i = 0;i < N - 11;i = i + 2)
			{
				place(i,N - 8,3);place(i,N - 7,5);place(i,N - 4,3);
				place(i,N - 3,5);place(N - 8,i,0);place(N - 7,i,6);
				place(N - 4,i,0);place(N - 3,i,6);
			}
		}
	}
}
int main()
{
	int _;
	read(_);
	while(_--)//在线读入
	{
		read(N);
		for(int i = 0;i < N;i++)
		for(int j = 0;j < N;j++)  
		    A[i][j] = 0;
		idx = 0;
		solve();
		int cnt = 0;
		for(int i = 0;i < N;i++)
		for(int j = 0;j < N;j++)
		    if(A[i][j] != 0) cnt++;//计算QM问号的个数🤔
		assert(cnt % 4 == 0);
		cnt /= 4;
		if(N % 2 == 1 && N >= 9) assert(N * N / 4 == cnt);
		cout<<cnt<<"\n";
		for(int i = 0;i < N;i++)
		for(int j = 0;j < N;j++)
		    cout<<A[i][j]<<(j + 1 == N ? "\n" : " ");//输出处理
	}
}

本来觉得在线处理会超，但是也过了，毕竟这道题的思维含量也不至于来卡我们的时间，怎么样，这么有趣的构造题，你学废怎么做了吗?~~~呃啊啊，好久没写专题博客了，最近得赶紧把旋转卡壳的下补上😄

Zz_0913

关注

13
点赞
踩
12

收藏

觉得还不错? 一键收藏
0
评论
有趣~2023 ICPC 亚洲区域赛南京站构造题 —— H.谜题（附带源码）

打过Codeforces的同学们都知道，CF上有一类非常锻炼思维的难题就是构造题，几乎每场div中都会有这样子的题目，构造题有很多种，比如：等等，这些都是非常直观的构造题，因为它们的构造对象非常的具象，然后还有一些比较抽象有难度的构造题，比如构造路线，游戏方案，博弈路径这些。然后在我们的ICPC-ACM等竞赛中，必定会出现一道构造题，往往是属于13道题目中的夺冠题，包括这次2023 ICPC 南京站中的H.谜题：在一个 n × n 的网格内不重叠地放入尽可能多的问号拼图（QM 拼
复制链接

扫一扫