2023 ICPC 亚洲区域赛南京站计算几何 —— Problem B.交并比(源代码出炉+解析）

   

     回想去年(2023)的亚洲区ICPC，由于我是学计算几何的，南京站的Problem.B——Intersection over Union让我印象颇深，这道题目我记得现场5个小时没有人写出来~，可以说难度非常大，妥妥的一道夺冠题~🤔，所以说在这里我简要讲一下解题思路以及源代码，其中的算法值得学习（就是ACM-ICPC这类竞赛的题目算法综合性很强），大家有空可以好好研究一下这道题O(∩_∩)O

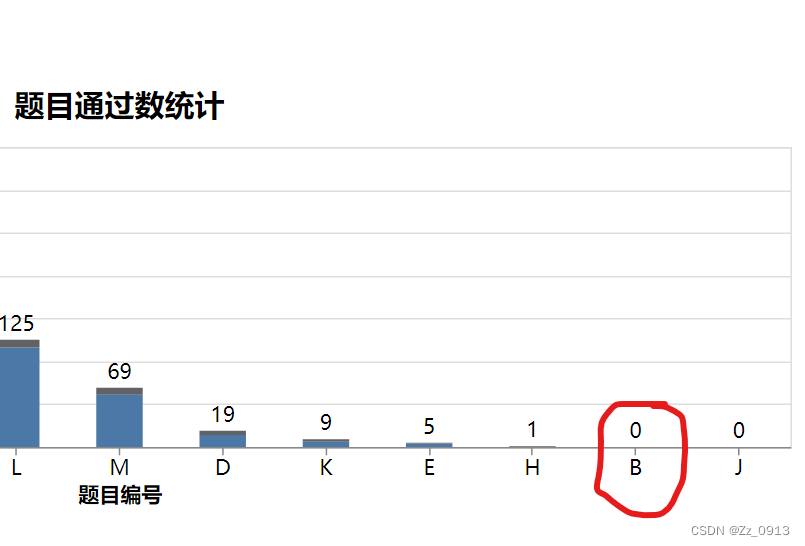
      那么我们先再上题目叭，在之前的某篇博文里有过，但是为了完整性（水~🤐），我再在这里放一次~[doge]👇：

       这次我们给出的是英文版的题目，大家只需要大致看懂即可，我直接放上简要的题意：

          首先我们来看一下这道题目的题意，简化后就是：

                1.给定一个矩形（OBB），要求找到一个坐标轴平行矩形（AABB） ；

                2.两个矩形的相交面积比上面积并就是所谓的交并比（IOU）；

                3.我们需要求出这个矩形使IOU最大。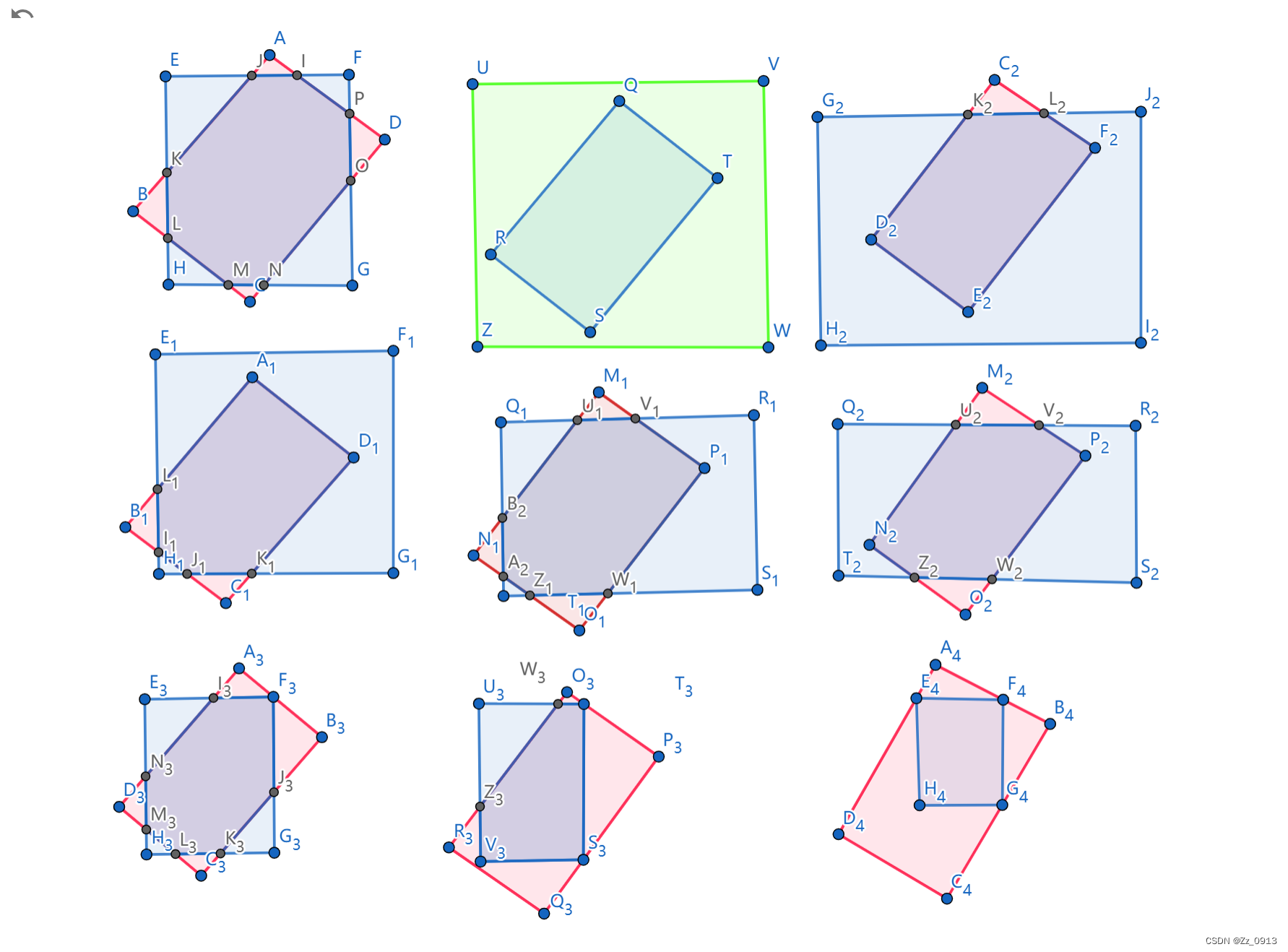、            👆：就是差不多这几种情况~，然后大家简略思考可以发现，这就是一道计               算几何中的函数极值问题🤔，那么一般思路就是👇：

       计算几何系列 —— 计算几何多边形求交&求并&求交并比以及一道难题（含AC代码）-CSDN博客

       然后，在之前写的博客👆中，我们通过非常复杂的代数方法证明关于IOU的这个函数是单峰函数，可以利用三分法，爬山法，梯度下降法等求解，都可以收敛到全局最优解，这边呢，我们使用三分法的一个代码，通过了QOJ，但是Codeforces目前出于TLE的状态（CF真的是强数据~），作为一个参考程序放出，供大家学习研究这道夺冠题，我做了非常详细的代码注释✌：

           👆：三分法，代码👇：

#include <bits/stdc++.h>
using namespace std;
const double Eps = 1e-18;//对于样例的精度设置
typedef long long LL;
typedef double LD;
typedef pair <int, int> pii;
#define cp const point &//点类
const LD eps = 0;//精度设置
int sgn (LD x) { return x > eps ? 1 : (x < -eps ? -1 : 0); }//符号判断
LD sqr (LD x) { return x * x; }//平方函数
struct point {
	LD x, y;
	point () {}
	point (LD xx, LD yy) { x = xx, y = yy; }
	point operator + (cp a) const { return {x + a.x, y + a.y}; }
	point operator - (cp a) const { return {x - a.x, y - a.y}; }
	point operator * (LD a) const { return {x * a, y * a}; }
	point operator / (LD a) const { return {x / a, y / a}; }
	point rot90() const { return {-y, x}; }//点关于原点逆时针旋转90度
	bool operator == (cp a) const {
		return x == a.x && y == a.y;	
	}
	void read() {
		int xx, yy;
		cin >> xx >> yy;
		x = xx, y = yy;
	}
};//有关计算几何点类的设置
LD det (cp a, cp b) { return a.x * b.y - b.x * a.y; }//向量叉积
LD dot (cp a, cp b) { return a.x * b.x + a.y * b.y; }//向量点积
LD dis (cp a, cp b) { return sqrt (sqr (a.x - b.x) + sqr(a.y - b.y)); }//距离公式
bool turn_left(cp a, cp b, cp c) {
	return sgn (det (b - a, c - a)) > 0;
}//判断是否三点左旋，小于零是右旋，也用于GrahamScan
#define cl const line &
struct line {
	point s, t;
	line () {}
	line (point ss, point tt) { s = ss, t = tt; }
	bool operator == (cl a) const {
		return s == a.s && t == a.t;
	}
};//两点式的直线类设置
point line_inter (cl a, cl b) {
	LD s1 = det (a.t - a.s, b.s - a.s);
	LD s2 = det (a.t - a.s, b.t - a.s);
	return (b.s * s2 - b.t * s1) / (s2 - s1);
}//判断并返回两直线的交点
bool turn_left (cl l, cp p) { return turn_left(l.s, l.t, p); }//判断点在直线的左侧
line h[8];
LD hpi_nosort() {
	line q[8]; 
    int l = 0, r = -1;
	point ret[8];
	q[0] = h[0]; q[1] = h[1]; r = 1;
	ret[1] = line_inter(q[0], q[1]);
	for (int t = 2; t < 8; t++) {
		auto &i = h[t];
		while (l < r && !turn_left(i, ret[r]))
			-- r;
		while (l < r && !turn_left(i, ret[l + 1]))
			++ l;
		++ r; q[r] = i;
		if (l != r) ret[r] = line_inter(q[r - 1], q[r]);
	}
	ret[l] = line_inter(q[r], q[l]);
	LD area = 0;
	for (int i = l; i <= r; i++) area += det(ret[i], ret[i == r ? l : i + 1]);
	return area;
}//hpi_nosort函数求出并返回H和P的Intersection，交面积，这个之前讲过，不细说了。
LD ans, sq;
LD check (LD x, LD y) {
	cout<<x<<' '<<y<<endl;
	h[1] = {{-1, -y}, {1, -y}};
	h[3] = {{x, -1}, {x, 1}};
	h[5] = {{1, y}, {-1, y}};
	h[7] = {{0, 1}, {0, -1}};
	LD a = hpi_nosort();
	LD f = x * y * 4; 
	return a / (f + sq - a);
}//check函数，三分法中的验证函数，求出xy轴矩形和输入矩形的交并比~
const LD Rp = (sqrt(5) - 1) / 2, Lp = 1 - Rp;//三分初始答案设置
LD check (LD x) {
	LD l = 0, r = 1, lv = -1, rv = -1, v = 0;
	for (int t = 42; t; t--) {//三分次数
		LD b = (r - l) * Rp;
		LD lmid = r - b, rmid = l + b;
		if (lv == -1) lv = check(x, lmid);
		if (rv == -1) rv = check(x, rmid);
		if (rv < lv) rv = lv, lv = -1, r = rmid;
		else lv = rv, rv = -1, l = lmid;
	}
	ans = max(ans, v = max(lv, rv));
	return v;
}//x的初步检验函数，用于三分y的值
void work() {
	vector <point> p;
	for (int i = 0; i < 4; i++) {
		point u; u.read();
		p.push_back(u);
	}
	if (!turn_left(p[0], p[1], p[2])) {
		reverse(p.begin(), p.end());
	}//边的旋转
	if (sgn(det(p[1] - p[0], {1, 0})) == 0 || sgn(det(p[2] - p[1], {1, 0})) == 0) {
		cout << "1\n";
		return;
	}
	auto center = (p[0] + p[2]) / 2;
	{
		int k = 0;
		for (int i = 0; i < 4; i++) {
			if (p[i].x < p[k].x) k = i;
		}
		vector <point> q;
		for (int i = 0; i < 4; i++) q.push_back(p[(i + k) % 4] - center);
		p = move(q);
	}//上述是对输入的四个点的重排
	
	sq = abs(det(p[1] - p[0], p[2] - p[1]));//求出一直矩形的面积
	
	LD Lx = p[2].x;
	LD Ly = p[3].y;
	for (auto &[x, y] : p) {//等比变换操作，这个是三分答案的基础
		x /= Lx;
		y /= Ly;
	}
	sq /= Lx * Ly;
	h[0] = {p[0], p[1]};
	h[2] = {p[1], p[2]};
	h[4] = {p[2], p[3]};
	h[6] = {p[3], p[0]};
	LD xl = 0, xr = 1, lv = -1, rv = -1;
	ans = check(1 - 1e-9);//三分初始答案的设置
	for (int t = 38; t; t--) {//三分次数，可以改
		LD b = (xr - xl) * Rp;
		LD lmid = xr - b, rmid = xl + b;
		if (lv == -1) lv = check(lmid);
		if (rv == -1) rv = check(rmid);
		if (rv < lv) rv = lv, lv = -1, xr = rmid;
		else lv = rv, rv = -1, xl = lmid;
	}//对于x的三分并验证
	check((xl + xr) / 2);
	cout << (double)ans << '\n'; 
}
int main() {
	ios::sync_with_stdio(false); cin.tie(0);//输入加速的设置，这边可以改快读
	int T = 1;
	cin >> T;
	cout << fixed << setprecision(10);
	for (int ca = 1; ca <= T; ca ++) {
		work();//不用我多说了~
	}
	return 0;
}

         对于一些高精度的处理，三分法其实时间复杂度还是偏大了👇，精度方面已经达到要求了：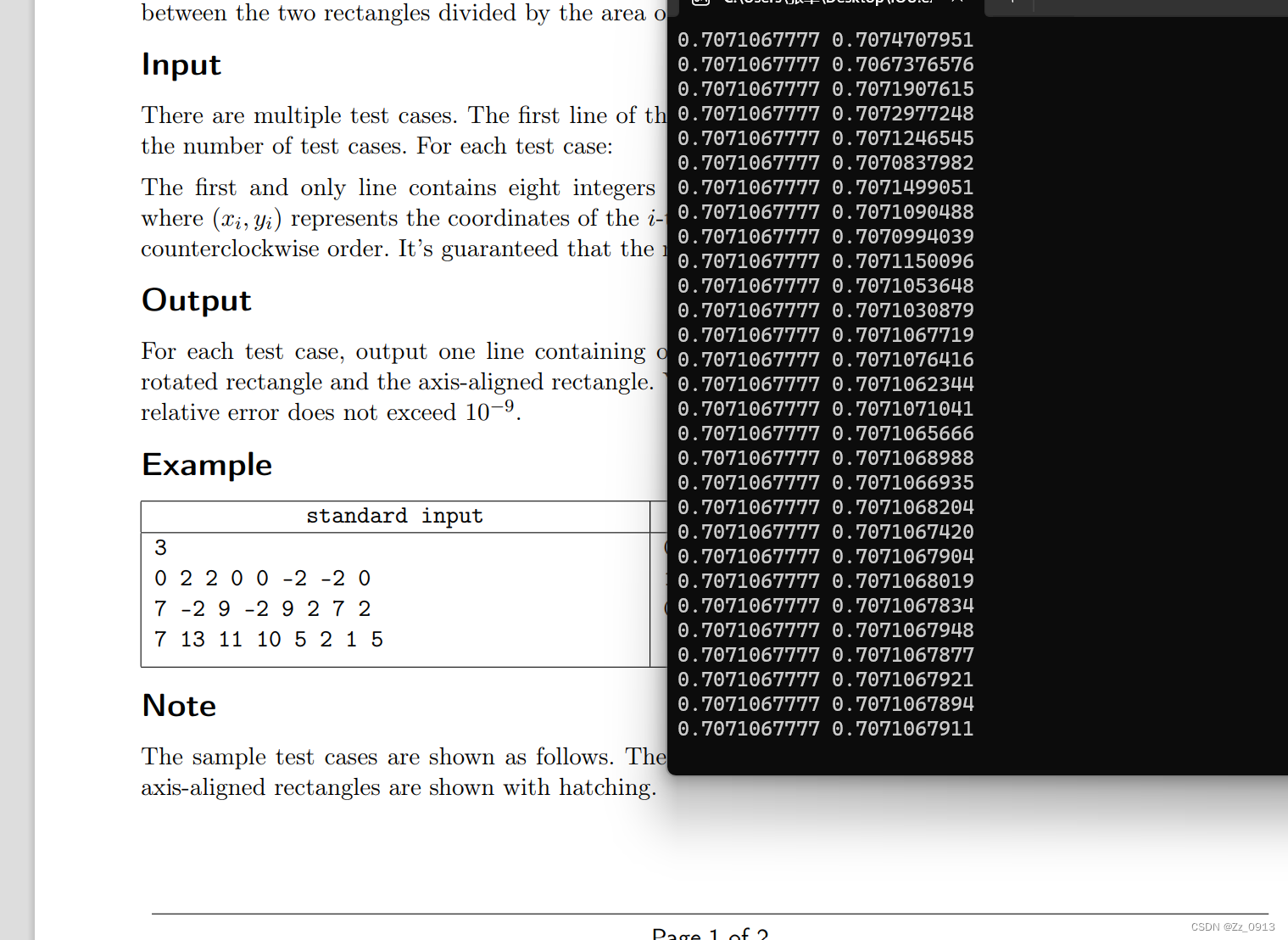

   希望大家能用其它更好的方法解决这道IOU，用三分差不多只能这样子，可能有些数据难过(｡･∀･)ﾉﾞ嗨，这一场挺水的😄