spss实现时间序列分析过程

在使用SPSS进行时间序列分析时，发现网上的信息量较少，而且不够全面，在这里记录一下学习心得，如有错误，望指正。

在进行时间序列分析之前，我们需要考察数据的一些性质，先附上百度百科的arima介绍：

ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），是时间序列预测分析方法之一。ARIMA(p，d，q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

这里面提到了几个关键性词语：

差分：在离散的情况下就是相邻两个元素的差，附一个讲解很细的网址：白话解释“差分”、“一阶差分” - 知乎

AR（自回归）：可以引申为自回归模型，这里通过自相关图得到P值

MA（滑动平均）：可以引申为滑动平均模型，这里通过偏相关得到Q值

这里判断PQ的值只能通过图得到一个简单的判断，具体还要看指标进行调试。这里附上一些判断的网址时间序列中p,d,q的确定 - 知乎，如何根据自相关（ACF）图和偏自相关（PACF）图选择ARIMA模型的p、q值_牛客博客，spss中ARIMA模型中参数的P，Q根据自相关的残差图和偏相关残差图怎么看的出来？_百度知道z

这里简述一下：先理解截尾和拖尾，截尾指并无逐渐收敛，但是在某一阶（就是图上的x坐标）突然趋于零，这里就是N阶截尾；拖尾指像一个尾巴一样，根部宽一点，越往后越细，全程并无明显的突变成0的阶，这里附上几个图：

在四阶之后突然趋于0，为四阶截尾

 

这个可以看出有一点拖尾但是在前面几个序列没有超过置信度上下限的，所以如果时拖尾(p,q)=(0,0)；这里我们可以明显看出有一些截尾，在2和4明显的趋于零，所以也可能是（2，2）（4，4）

引用自如何根据自相关（ACF）图和偏自相关（PACF）图选择ARIMA模型的p、q值_牛客博客 (nowcoder.net)

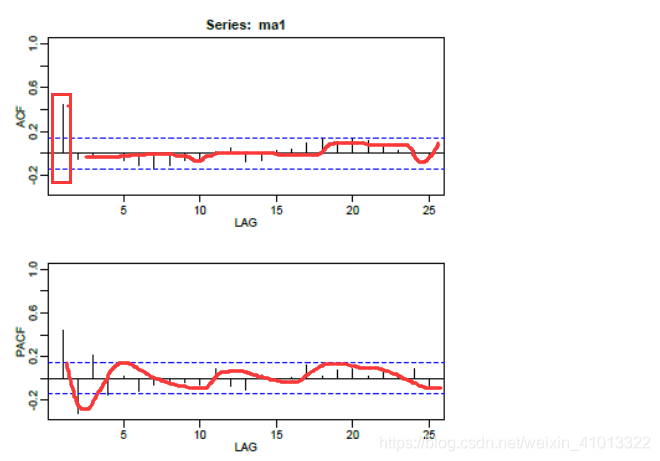
这里可以看出很明显的拖尾，同时在开始阶段也有超过置信区间的阶，所以我们初步判断为一阶拖尾（ACF），和2或3阶截尾（PACF)

之后我们就需要了解整个时间序列的过程：（引自百度百科）

时间序列的预处理包括两个方面的检验，平稳性检验和白噪声检验。能够适用ARMA模型进行分析预测的时间序列必须满足的条件是平稳非白噪声序列。对数据的平稳性进行检验是时间序列分析的重要步骤，一般通过时序图和相关图来检验时间序列的平稳性。时序图的特点是直观简单但是误差较大，自相关图即自相关和偏自相关函数图相对复杂但是结果更加准确。本文先用时序图进行直观的判断再利用相关图进行更进一步的检验。对于非平稳时间序列中若存在增长或下降趋势，则需要进行差分处理然后进行平稳性检验直至平稳为止。其中，差分的次数就是模型ARIMA(p,d,q)的阶数，理论上说，差分的次数越多，对时序信息的非平稳确定性信息的提取越充分，但是从理论上说，差分的次数并非越多越好，每一次差分运算，都会造成信息的损失，所以应当避免过分的差分，一般在应用中，差分的阶数不超过2。

到这里知识准备过程已经结束了，下面是具体操作：这里附上一个百度经验网址https://jingyan.baidu.com/article/48a42057e664bda9242504f8.html

具体操作完全可以参考这个来。

下面介绍自己做的全过程：

先找d值：（就是几阶差分拥有平稳性）

 不平稳，进行一阶差分的序列图分析：

很平稳，所以d=1; （阶数越高是会有更好平稳性，但是会丢失很多信息）

然后我们进行平稳性检验：

 

自相关图和偏相关图在大致都在置信度区间内，所以符合平稳性检验（这里是更准确的平稳性检验）然后我们判断一下PQ，最后得出（p,d,q)=(4,1,4)/(2,1,2)/(0,1,0)这几个可能值（在前面例子中提到了判断方法） 

然后我们就可以时间序列分析啦，先选择专家分析，让SPSS给你一个推荐的（p，d，q）值

这里我给出的专家建议结果如下

 

 

 可以看出给的建议是（（0，1，0），（1，0，0）（这个是季节性的arima部分））。然后看圈出来的指标

 这里的R是表示拟合度很好的，显著性低于0.01是表示最后得到的系数比较显著，应该不等于0的。

然后做了一下airma（2，1，2）

 它的R更大，而且显著性趋近于0.000更好一点，所以可以反复调试得到结果（同时在这个参数下，根据指导的网址，我们可以得出方程）

还有就是一个有关显示预测的网址：

SPSS中出现“由于不能计算任何预测 因此为创建预测表” 是什么意思_百度知道