时间序列分析的核心在于理解发展水平和发展速度的计算方法,以及如何利用这些指标进行预测和决策。本文提供详细的数学方法、计算公式和示例,帮助你全面掌握时间序列分析的一般步骤。
一、发展水平的计算方法
发展水平(Development Level)指的是某一时刻或某一时期的数据值,主要用于衡量整体规模。
1. 原始数据(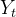 )
)
-
直接使用时间序列数据本身,如 GDP、销售额、气温等。
-
示例:某公司过去 5 年的销售额(单位:万元)
Y=[100,120,140,160,180]
2. 移动平均(Moving Average)
-
计算多个时间点的数据均值,用于平滑波动,消除季节性或短期波动影响。
-
简单移动平均(SMA):
-
加权移动平均(WMA)(赋予近期数据更高权重):
示例:计算过去 3 期的简单移动平均:
二、发展速度的计算方法
发展速度(Growth Rate)用于衡量时间序列的变化速率,常见计算方法包括:
1. 绝对增长量(Absolute Growth)
-
计算时间序列相邻或某一固定基准期的数据差异:
-
示例:
2. 发展速度指标
(1) 环比增长率(Month-over-Month Growth Rate, 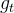 )
)
-
衡量相邻两个时期的增长率:
-
示例:
(2) 同比增长率(Year-over-Year Growth Rate, 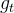 )
)
-
衡量某一时期与上一年(或固定基准)的增长率:
(kk 一般取 12 个月或 1 年)
示例:如果 2023 年销售额为 180 万,2022 年为 140 万:
(3) 平均增长率(CAGR,Compound Annual Growth Rate)
-
衡量整体时间序列的年均增长率:
-
示例:公司 5 年销售额从 100 增长到 180:
三、时间序列分析的一般步骤
时间序列分析通常包括以下步骤:
1. 数据预处理
-
缺失值处理:使用插值、均值填充或删除异常数据。
-
平稳性检测:采用ADF 检验或KPSS 检验来判断时间序列是否平稳。
-
去趋势:对非平稳序列进行差分或回归去趋势处理。
2. 发展水平分析
-
计算原始数据、移动平均、趋势分析等,以了解数据的整体变化情况。
3. 发展速度分析(一般的课本爱讲)
-
计算增长率(同比、环比)、平均增长率,判断数据变化趋势。
4. 模型拟合
-
ARIMA 模型(自回归积分滑动平均)用于预测长期趋势:
-
指数平滑(Exponential Smoothing):
-
简单指数平滑:
-
霍尔特线性趋势:适用于增长趋势的数据。
-
霍尔特-温特斯季节性模型:适用于具有季节性周期的数据。
-
5. 预测与决策
-
通过时间序列模型(如 ARIMA、SARIMA、LSTM)预测未来数据,并基于结果制定策略。
四、综合示例
假设某企业的季度销售额数据如下(单位:万元):
Y=[100,120,140,160,180,210,250,280]
计算关键指标
-
计算环比增长率:
-
计算同比增长率(假设为季度数据,对比上一年同季度):
-
计算平均增长率:
-
移动平均(过去 3 期):
五、总结
-
发展水平用于衡量数据规模,常用方法包括原始值、移动平均、趋势分析等。
-
发展速度衡量数据变化,主要方法有绝对增长量、环比/同比增长率、平均增长率等。
-
结合模型分析,如 ARIMA、指数平滑等,进行预测。
-
实际应用:广泛用于经济分析、销售预测、市场趋势判断等。
由这些方法后,你可以全面分析时间序列数据,预测未来趋势,做出科学决策。























 4842
4842

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








