LeetCode 热题 HOT 100 题解（仅记录解题思路）

方法一：哈希

首先将A的所有结点存储在哈希表中，接着遍历B，如果B的某个结点存在于哈希表中，则证明相交；

方法二：双指针

指针p1从A的头结点出发，指针p2从B的头结点出发；当p1不为null时，指向下一个；当p1为null时，指向B的开始。p2同理。直到2个指针指向同一个结点（有交点）或者同时指向为null（无交点）。

234. 回文链表

方法一：将值复制到数组中后用双指针法

方法二：快慢指针

指针p1和p2开始都指向第一个结点，然后p1每次移动1步，p2则2步，当p2移到末尾时，则p1到中间位置，接着反转后半部分，并与前半部分比较。

226. 翻转二叉树

方法一：递归

如果左右两棵子树都已实现了反转，那么仅仅交换其位置即可。

206. 反转链表

方法一：递归

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

169. 多数元素

方法一：哈希

遍历一遍数组nums，存在哈希表中，相同元素+1；接着再遍历一次哈希表，找出最大值

方法二：排序

对数组进行排序，那么下标为 ⌊n/2⌋ 的元素（下标从 0 开始）一定是众数。

方法三：随机化

随机挑选一个值，检查其是否是众数；不是则重新随机。

141. 环形链表

方法一：哈希表

从头结点出发，检索当前结点是否在哈希表中，若不再，则加入；若在，则表示有环

方法二：快慢指针

指针p1在头结点处，指针p2在头结点的next处，然后p1每次移动1格，p2则走2步，若在其中一个进入null之前两者指向同一结点，则代表有环。

136. 只出现一次的数字

方法一：集合增删

使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。

方法二：哈希

使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。

方法三：集合求和

使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

方法四：位运算

因此对于出现次数为偶数的元素，执行连续位运算的最后结果是0，而对于出现次数为奇数的元素，最后当然就被保存下来了。

C++ 提供了 6 种位运算符，包括按位与（&）、按位或（| ）、按位异或（^）、取反（~）、左移（<<）、右移（>>）

拓展题：一个数组中，只有2个数出现了1次，其他所有数都出现了2次，那么如何在保证空间复杂度尽可能低的情况下快速找到这两个数呢？

答：这道题可以拓展到只有2个数出现了奇数次，其他所有数都出现了偶数次。采用集合增删、哈希、集合求和方法的时间复杂度为O(n)，空间复杂度也为O(n)。如果要使得空间复杂度尽可能低，需要考虑进行异或运算。

异或运算具备的性质是：任何数和其自身做异或运算，结果是 0；任何数和 0 做异或运算，结果仍然是原来的数；异或运算满足交换律和结合律。

因此可以将x初始化为0，然后对数组中的数依次与x执行异或运算，最后得到的结果就是x=a⊕b。

接下来要考虑如何把x拆分开得到a和b。举个例子，如果x=a⊕b=>11010(二进制形式表示)，那么就说明a和b的第2位（从低到高）必然有一个数该位是1，另一个数该位是0。我们可以将这个1提取出来得到y=>x&(-x)或者y=>x-x&(x-1)得到y=00010，初始化z为0，接着对数组中的元素a依次进行操作，如果a&y!=0，就将其与z进行异或操作（相当于是把第2位为1的数单独拎出来做异或运算），最后得到的结果必然是a和b的其中一个，再将其与x进行异或即可得到另一个数，这样的空间复杂度为O(1)。

461. 汉明距离

方法一：使用内置函数

__builtin_popcount(a^b)

方法二：移位实现位计数

while (s) {
ret += s & 1;
s >>= 1;
}

方法三：每次都去掉最右侧的1

while (s) {
s &= s - 1;
ret++;
}

448. 找到所有数组中消失的数字

方法一：哈希

方法二：直接对数组进行修改

具体来说，遍历 nums，每遇到一个数 x，就让 nums[x−1] 增加 n。由于 nums 中所有数均在 [1,n] 中，增加以后，这些数必然大于 n。最后我们遍历 nums，若 nums[i] 未大于 n，就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。

338. 比特位计数

方法一：移位实现位计数

方法二：每次都去掉最右侧的1

方法三：动态规划——最高有效位

不同于暴力搜索，动态规划是一种用一个状态代表一类情况的方法。我们观察到对于1011而言，其1的位数其实相当于(1011-1000)中1的位数+1。我们称1、10、100、1000这种2的整数次幂代表最高有效位highBit。状态转移公式为bits[i]=bits[i−highBit]+1。而一个数是否是最高有效位只需要通过i&(i-1)==0判断即可。

方法四：动态规划——最低有效位

奇数中1的个数 = 偶数(奇数-1)中1的个数 + 1；例如 111 110

偶数中1的个数 = 偶数/2中1的个数；例如 1000 100

因此状态转移方程为bits[i]=bits[i>>1]+i&1

方法五：动态规划——最低设置位

我们观察到对于1011而言，其1的位数相当于去掉最右侧1后1010中1的位数+1。状态转移公式为bits[i]=bits[i&(i-1)]+1。

121. 买卖股票的最佳时机

方法一：一次遍历

假设我们要在第i天卖出股票，那么自然我们希望股票是在这天之前的低谷买入的，因此我们只需要在遍历的同时维护一个前面天中的低谷，不断更新即可。

283. 移动零

方法一：双指针法

使用双指针，左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。

右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。

注意到以下性质：

左指针左边均为非零数；

右指针左边直到左指针处均为零。

因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。

543. 二叉树的直径

方法一：DFS

首先我们知道一条路径的长度为该路径经过的节点数减一，所以求直径（即求路径长度的最大值）等效于求路径经过节点数的最大值减一。

而任意一条路径均可以被看作由某个节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到。

21. 合并两个有序链表

方法一：递归（也可以认为是双指针）

20. 有效的括号

方法一：用栈模拟即可

617. 合并二叉树

方法一：DFS

可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树，并将对应的节点进行合并。

两个二叉树的对应节点可能存在以下三种情况，对于每种情况使用不同的合并方式。

如果两个二叉树的对应节点都为空，则合并后的二叉树的对应节点也为空；

如果两个二叉树的对应节点只有一个为空，则合并后的二叉树的对应节点为其中的非空节点；

如果两个二叉树的对应节点都不为空，则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和，此时需要显性合并两个节点。

对一个节点进行合并之后，还要对该节点的左右子树分别进行合并。这是一个递归的过程。

104. 二叉树的最大深度

方法一：DFS

如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为max(l,r)+1。而左子树和右子树的最大深度又可以以同样的方式进行计算。

因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

101. 对称二叉树

方法一：递归

94. 二叉树的中序遍历

方法一：递归

1. 两数之和

方法一：哈希

70. 爬楼梯

方法一：动态规划

方法二：矩阵快速幂

方法三：通项公式

中等（66道）：

236. 二叉树的最近公共祖先

方法一：递归

方法二：存储父结点然后向上遍历

739. 每日温度

方法一：暴力

反向遍历温度列表。对于每个元素 temperatures[i]，在数组 next 中找到从 temperatures[i] + 1 到 100 中每个温度第一次出现的下标，将其中的最小下标记为 warmerIndex，则 warmerIndex 为下一次温度比当天高的下标。如果 warmerIndex 不为无穷大，则 warmerIndex - i 即为下一次温度比当天高的等待天数，最后令 next[temperatures[i]] = i。

例如，反向遍历开始，对于73而言，从74~100全是无穷大，因此res[7]=0，next[73]=7；接着是76，从77~100全是无穷大，因此res[6]=0，next[76]=6；接着是72，从73~100发现角标最小的是next[76]=6，因此res[5]=next[76]-5=1，next[72]=5，其他以此类推。

方法二：单调栈

当我们聚焦在某个元素x上时，我们只关心在x右侧且比x值要大的离x最近的值。例如75，71，69，72，76，78，对于75而言，我们只关心76的存在，75~76中间的其他值对75都没意义。因此我们可以开辟一个单调栈，从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里，则表示尚未找到下一次温度更高的下标。

221. 最大正方形

方法一：暴力

将每一个方格分别视为正方形的左上角，如果是0，继续下一个；如果是1，开始尝试延申边长，并加以判断是否满足全为0的条件。

方法二：动态规划

我们用 dp(i,j) 表示以 (i,j) 为右下角，且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i,j) 的值，那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值，其平方即为最大正方形的面积。

先来阐述简单共识

若形成正方形（非单 1），以当前为右下角的视角看，则需要：当前格、上、左、左上都是 1
可以换个角度：当前格、上、左、左上都不能受 0 的限制，才能成为正方形

上面详解了三者取最小的含义：

图 1：受限于左上的 0
图 2：受限于上边的 0
图 3：受限于左边的 0
数字表示：以此为正方形右下角的最大边长
黄色表示：格子 ? 作为右下角的正方形区域
就像木桶的短板理论那样——附近的最小边长，才与 ? 的最长边长有关。

如上图所示，状态转移方程为：

注意对于边缘元素（i==0||j==0)要记得初始化为1，否则就执行上述的状态转移方程即可。

215. 数组中的第K个最大元素

方法一：快排（不用sort，手搓找到第k个最大元素即可）

方法二：构建大顶堆，做 k−1 次删除操作后堆顶元素就是我们要找的答案。

208. 实现 Trie (前缀树)

方法一：字典树

参见：AcWing 835. Trie字符串统计 - AcWing

207. 课程表

对于图 G 中的任意一条有向边 (u,v)，u 在排列中都出现在 v 的前面。那么称该排列是图 G 的「拓扑排序」。只要u在排列中都出现在v的前面，那么一定可以完成所有的课程。只要不存在环即可。

因此我们就可以将本题建模成一个求拓扑排序的问题了：

我们将每一门课看成一个节点；
如果想要学习课程 A 之前必须完成课程 B，那么我们从 B 到 A 连接一条有向边。这样以来，在拓扑排序中，B 一定出现在 A 的前面。

方法一：

求拓扑序列最简单的方法就是BFS了，建立一个队列，先找到入度为0的点，放入队列中，然后出队（放入答案中），并将其临近结点的入度减1，如果某个相邻节点 v 的入度变为 0，那么我们就将 v 放入队列中。然后重复上述操作，直到最后的答案中包含这n个结点，我们便得到了拓扑序列。

方法二：3种状态表示（未搜索、已搜索、搜索中）＋DFS。

200. 岛屿数量

方法一：DFS

我们可以将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边相连。

为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 1，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0。

最终岛屿的数量就是我们进行深度优先搜索的次数。

方法二：BFS

为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 1，则将其加入队列，开始进行广度优先搜索。在广度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0。直到队列为空，搜索结束。

最终岛屿的数量就是我们进行广度优先搜索的次数。

方法三：并查集

为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 1，则将其与相邻四个方向上的 1 在并查集中进行合并。

最终岛屿的数量就是并查集中连通分量的数目。

198. 打家劫舍

方法一：动态规划

上述方法使用了数组存储结果。考虑到每间房屋的最高总金额只和该房屋的前两间房屋的最高总金额相关，因此可以使用滚动数组，在每个时刻只需要存储前两间房屋的最高总金额。

238. 除自身以外数组的乘积

方法一：左右乘积列表

我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案（因为这会涉及到0的问题），而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。

优化：先把输出数组当作 L 数组来计算，然后再动态构造 R 数组得到结果，空间复杂度为O(1)

方法二：双指针

其实本质和方法一的思想类似，不过我们并不需要显式地求得L和R，设立两个指针left和right分别指向最左和最右的元素，设置左部和右部乘积为1，然后更新answer数组，在这个过程中，left++，right--，左部和右部乘积也不断更新。因此，整体来看，answer数组中的每一个元素都是其左部乘积和右部乘积相乘的结果。
    int left = 0, right = nums.size() - 1;
    int lp = 1, rp = 1;
    while (right >= 0 && left < nums.size()) {
        answer[right] *= rp;
        answer[left] *= lp;
        lp *= nums[left++];
        rp *= nums[right--];
    }

155. 最小栈

方法一：辅助栈

152. 乘积最大子数组

方法一：dp

方法二：结论法

结论：一个不包含0的整数序列的连续乘积最大值，一定以起点开始或者以终点结束。

反证法：假设最大子数组乘积是在中间，那么两边一共有4种情况，分别一正一负，一负一正，两负，两正，无论哪种都有让他变更大的可能。

但是我们题目中并没提到保证没有非0元素呀！

因此，我们在比较过后运算时需要将原始数组中的0变为1，相当于原始数组遇到0就进行截断处理。因此只需要向左、向右分别遍历一遍找到最大值即可。
class Solution {
   public int maxProduct(int[] nums) {
       int product = 1, n = nums.length;
       int max = nums[0];

       for(int i = 0;i < n;i++){
           product *= nums[i];
           max = Math.max(max, product);
           if(nums[i] == 0){
               product = 1;
           }
       }

       product = 1;
       for(int i = n - 1;i >= 0;i--){
           product *= nums[i];
           max = Math.max(max, product);
           if(nums[i] == 0){
               product = 1;
           }
       }

       return max;
   }
}

148. 排序链表

方法一：自顶向下归并排序

方法二：自底向上归并排序

146. LRU 缓存

方法一：哈希表＋双向链表

142. 环形链表 II

在之前的环形链表题中，我们只需要判断该链表中是否存在环即可，但本题却让给出入环结点的下标。

方法一：哈希表

但是该方法的时间复杂度和空间复杂度都是O(N)

方法二：快慢指针

139. 单词拆分

方法一：dp

初始思路：字符串从头开始遍历子字符串，遇到字典内有的单词则直接从字符串内删掉，最后看看是否整个字符串都能删完即可。

但这样做肯定是有问题的，没有考虑到如下的情况： s ="goalspecial" wordDict =["go","goal","goals","special"] 当字符串中的一个子字符串包含有多个字典中的词，则需要考虑究竟要使用哪个词了。

647. 回文子串

方法一：中心拓展

方法二：Manacher 算法

方法三：dp

dp[i][j]表示 i 到 j 的字符串能不能构成回文串,那么dp[i][j] = dp[i +1][j - 1] && (s[i] == s[j])

128. 最长连续序列

方法一：哈希表

322. 零钱兑换

方法一：记忆化搜索

方法二：dp

494. 目标和

方法一：回溯（暴力枚举）

方法二：dp

此外，关于背包容量的选取哪个最优？

438. 找到字符串中所有字母异位词

方法一：滑动窗口

当然也可以不用数组，用哈希表

方法二：优化的滑动窗口

437. 路径总和 III

方法一：dfs

时间复杂度为O(n^2)

方法二：前缀和

时间复杂度为O(n)

416. 分割等和子集

方法一：dp（0-1背包变形——小于等于=>恰好）

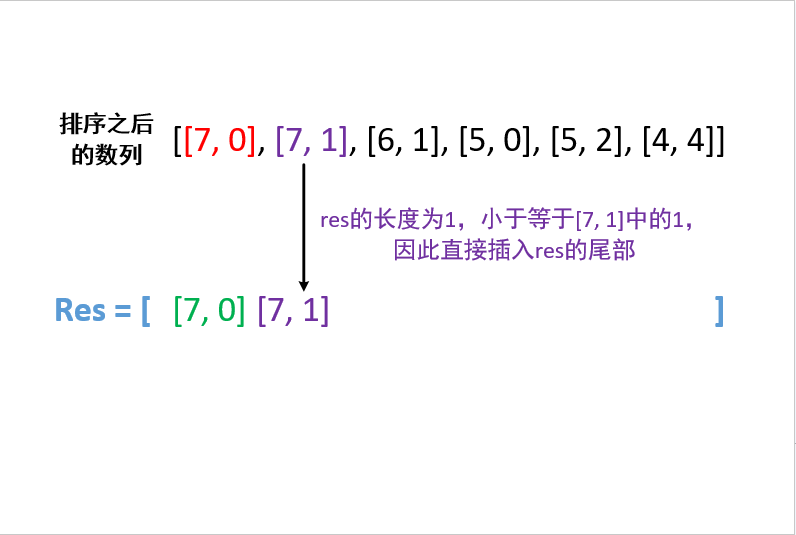
406. 根据身高重建队列

本题题意不太好理解，需要仔细品读

解题关键：高个子经过排序优先固定位置，然后让矮个子根据自己的k主动插入进去

方法一：排序后append|insert

399. 除法求值

方法一：bfs

方法二：Floyd 算法

方法三：带权并查集

394. 字符串解码

方法一：单栈操作

方法二：双栈操作

在方法一的基础上，分别建立一个字符串栈（注意存的是字符串）和数字栈，这样就省去了大量的单个字符出栈然后反转之类的操作，其他思想一致

方法三：递归

347. 前 K 个高频元素

方法一：小顶堆

方法二：模拟快速排序

337. 打家劫舍 III

方法一：dp

309. 买卖股票的最佳时机含冷冻期

方法一：dp

300. 最长递增子序列

方法一：dp

方法二：贪心+二分

287. 寻找重复数

方法一：二分

方法二：二进制

方法三：快慢指针

279. 完全平方数

方法一：dp

方法二：数学

253. 会议室 II

方法一：最小堆

可以按照开始时间顺序对数组进行排序，接着将第一个会议的结束时间加入最小堆（这表示目前我们有一个会议室被占用，直到这个时间点），接着依次遍历，从第二个开始，如果当前会议的开始时间大于等于最小堆中的最早结束时间，说明这个会议室可以被重复利用，因此我们可以用当前会议的结束时间对堆顶元素进行替换；如果前会议的开始时间小于最小堆中的最早结束时间，说明需要新增一个会议室，直接将当前会议的结束时间入堆即可。

最后所需会议室的最小数量就等于遍历结束时堆中元素的数量。

方法二：扫描线

将会议的开始时间和结束时间分别存储并升序排序，使用两个指针分别跟踪开始时间和结束时间。接着遍历所有的时间点，并维护当前所需会议室的数量，在遍历过程中得到其max值，如果当前的开始时间小于当前的结束时间，表示新的会议开始了，需要一个新的房间; 如果当前的开始时间大于等于当前的结束时间，表示一个会议已经结束，可以释放一个房间

240. 搜索二维矩阵 II

方法一：暴搜

我们直接遍历整个矩阵 matrix，判断 target 是否出现即可。

方法二：二分查找

由于矩阵 matrix 中每一行的元素都是升序排列的，因此我们可以对每一行都使用一次二分查找，判断 target 是否在该行中，从而判断 target 是否出现。

方法三：Z字型查找

22. 括号生成

方法一：递归＋回溯

用left和right记录剩余的左、右括号数量（初始化为n）

两者都为0时，将当前字符串str加入到res中；
剩余左右括号数相等，下一个只能用左括号；
剩余左括号小于右括号，下一个可以用左括号也可以用右括号。

49. 字母异位词分组

方法一：排序后字符串哈希

由于互为字母异位词的两个字符串包含的字母相同，因此对两个字符串分别进行排序之后得到的字符串一定是相同的，故可以将排序之后的字符串作为哈希表的键。

方法二：计数后数组哈希

由于互为字母异位词的两个字符串包含的字母相同，因此两个字符串中的相同字母出现的次数一定是相同的，故可以将每个字母出现的次数使用字符串表示，作为哈希表的键。

由于字符串只包含小写字母，因此对于每个字符串，可以使用长度为 26 的数组记录每个字母出现的次数。

48. 旋转图像

方法一：原地旋转

方法二：用翻转代替旋转

46. 全排列

方法一：交换回溯法

方法二：标记回溯法（空间开销较大）

class Solution {
private:
    vector<vector<int>> res;
    vector<int> path;
    void backtracing(vector<int>& nums,vector<int>& record){
        if(path.size()==nums.size()){
            res.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(record[i]==0){ //i未记录，表示i指示的数在该节点可用
                path.push_back(nums[i]);
                record[i]=1;  //表示在深入过程的下一节点不可用
                backtracing(nums,record);
                path.pop_back(); //回溯
                record[i]=0; //恢复 
            }
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<int> record(nums.size(),0);
        backtracing(nums,record);
        return res;
    }
};

39. 组合总和

方法一：搜索回溯

34. 在排序数组中查找元素的第一个和最后一个位置

方法一：二分查找

33. 搜索旋转排序数组

方法一：分为两部分对其进行二分查找

定理一：只有在顺序区间内才可以通过区间两端的数值判断target是否在其中。
定理二：判断顺序区间还是乱序区间，只需要对比 left 和 right 是否是顺序对即可，left <= right，顺序区间，否则乱序区间。
定理三：每次二分都会至少存在一个顺序区间。
通过不断的用Mid二分，根据定理二，将整个数组划分成顺序区间和乱序区间，然后利用定理一判断target是否在顺序区间，如果在顺序区间，下次循环就直接取顺序区间，如果不在，那么下次循环就取乱序区间。

方法二：先找轴点（最小值）再二分

举个例子，对于[4,5,6,7,0,1,2]而言，我们可以以4作为衡量标准，通过二分查找到第一个小于4的元素即得到最小值0（纵然[5,6,7,0,1,2]并非完全有序）；

接着让l为0的下标idx，r为l+n-1（你可能会好奇这不是超过数组范围了吗，但其实后续正是要通过取余来使得原本旋转的数组重新变得有序），通过二分找到答案即可。
class Solution {
    public int search(int[] nums, int target) {
        int min = 0, n = nums.length;
        for (int l = 1, r = n - 1; l <= r;) {
            int m = (l + r) / 2;
            if (nums[0] < nums[m]) l = m + 1;
            else { r = m - 1; min = m; }
        }
        for (int l = min, r = l + n - 1; l <= r;) {
            int m = (l + r) / 2, i = m % n;
            if (target < nums[i]) r = m - 1;
            else if (target > nums[i]) l = m + 1;
            else return i;
        }
        return -1;
    }
}

31. 下一个排列

方法一：两遍扫描

538. 把二叉搜索树转换为累加树

方法一：反序中序遍历

方法二：Morris遍历

class Solution {
    public TreeNode convertBST(TreeNode root) {
        int sum = 0;
        TreeNode node = root;
        //借鉴线索二叉树的思想，充分利用二叉树中的空指针。考虑到遍历顺序为右中左，故当前节点的右子树遍历结束后应当遍历当前节点，故应将当前节点右子树中最后遍历的节点的左指针指向当前节点，即建立右孩子到父节点的联系，而其右子树最后遍历的节点一定为右子树中最左侧节点。
        while (node != null){
            if (node.right == null){//当前节点没有右孩子，优先遍历当前节点
                sum += node.val;
                node.val = sum;
                node = node.left;//当前节点遍历结束，继续遍历其后继节点
            } else {
                TreeNode succ = getSuccessor(node);//寻找当前节点的前驱节点
                if (succ.left == null){//如果前驱节点左指针为空，将其指向当前节点，方便从当前节点的右子树寻找当前节点
                    succ.left = node;
                    node = node.right;//控制权优先转交给其右孩子
                } else {//前驱节点左指针不为空，即已经建立线索
                    succ.left = null;//拆除当前节点的前驱节点的线索还原二叉树（该节点已经在上一次循环中被访问过，其左指针不再需要）
                    sum += node.val;//遍历当前节点
                    node.val = sum;
                    node = node.left;//继续遍历后继节点
                }
            }
        }
        return root;
    }
    //建立一个函数寻找当前节点的前驱节点。
    public TreeNode getSuccessor(TreeNode node){
        TreeNode succ = node.right;
        //前驱节点一定在当前节点右子树的最左端，或前驱节点的左指针已经指向当前节点
        while (succ.left != null && succ.left != node){
            succ = succ.left;
        }
        return succ;
    }
    
}

560. 和为 K 的子数组

方法一：枚举

方法二：前缀和 + 哈希表优化

使用前缀和的方法可以解决这个问题，因为我们需要找到和为k的连续子数组的个数。通过计算前缀和，我们可以将问题转化为求解两个前缀和之差等于k的情况。
假设数组的前缀和数组为prefixSum，其中prefixSum[i]表示从数组起始位置到第i个位置的元素之和。那么对于任意的两个下标i和j（i < j），如果prefixSum[j] - prefixSum[i] = k，即从第i个位置到第j个位置的元素之和等于k，那么说明从第i+1个位置到第j个位置的连续子数组的和为k。
通过遍历数组，计算每个位置的前缀和，并使用一个哈希表来存储每个前缀和出现的次数。在遍历的过程中，我们检查是否存在prefixSum[j] - k的前缀和，如果存在，说明从某个位置到当前位置的连续子数组的和为k，我们将对应的次数累加到结果中。
这样，通过遍历一次数组，我们可以统计出和为k的连续子数组的个数，并且时间复杂度为O(n)，其中n为数组的长度。

19. 删除链表的倒数第 N 个结点

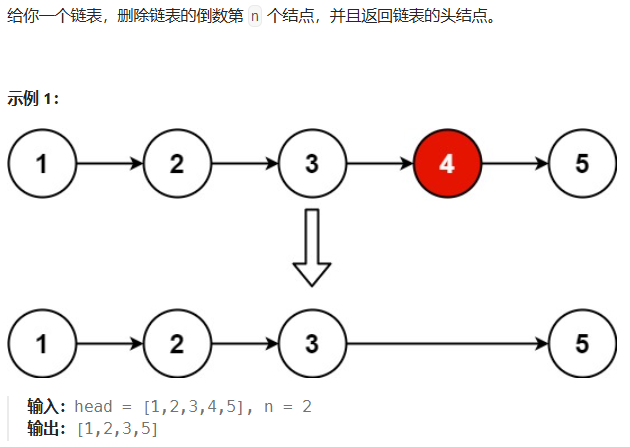
方法一：计算链表长度

方法二：栈

方法三：双指针

17. 电话号码的字母组合

方法一：回溯

15. 三数之和

方法一：三重循环

直接套三重循环，但代价是需要用到哈希表去重，时间和空间复杂度都很高

方法二：三重循环优化——排序

方法一存在遍历重复的问题，「不重复」的本质是什么？我们保持三重循环的大框架不变，只需要保证：

第二重循环枚举到的元素不小于当前第一重循环枚举到的元素；

第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。

如何实现呢？

首先对其进行排序，接着保证单重循环内相邻两次枚举的元素不能相同即可。

但时间复杂度仍然较高。

方法三：三重循环优化——双指针

11. 盛最多水的容器

方法一：双指针

最大水量=Math.min(height[left],height[right])*长度，往中间移动长度一定会变短

如果移动高的那一边，会有两种情况：

1、下一根柱子的高度比现在高，高度还取最小值低的那边，最大水量比原来小

2、下一根柱子的高度比现在低，高度比原来的最小值还小，最大水量比原来小

如果移动低的那一边，会有两种情况：

1、下一根柱子的高度比现在高，高度就可以取更高的值，最大水量不一定比原来小

2、下一根柱子的高度比现在低，高度比原来的最小值还小，最大水量比原来小

所以应该移动低的那一边

5. 最长回文子串

方法一：动态规划

方法二：中心扩展

方法三：Manacher 算法

3. 无重复字符的最长子串

方法一：滑动窗口

直观的想法就是“把求解最长子字符串的问题 ,转化为求解两个重复字符间的最长距离”

2. 两数相加

方法一：模拟

79. 单词搜索

方法一：回溯

方法二：方法一基础上的剪枝

114. 二叉树展开为链表

方法一：前序遍历

方法二：寻找前驱节点

直接把左子树的最右节点连接到根的右节点，再把根的右子树连接改成左子树，根移动到右节点，依次循环到null也就是右子树的底部

方法三：反前序遍历

将前序遍历反过来遍历，那么第一次访问的就是前序遍历中最后一个节点。那么可以调整最后一个节点，再将最后一个节点保存到pre里，再调整倒数第二个节点，将它的右子树设置为pre，再调整倒数第三个节点，依次类推直到调整完毕。
class Solution {
public:
    TreeNode* preNode;
    void flatten(TreeNode* root) {
        if (root == NULL) return;
        flatten(root->right);
        flatten(root->left);
        root->left = NULL;
        root->right = preNode;
        preNode = root;
    }
};

621. 任务调度器

方法一：模拟

方法二：构造（想法很巧妙）

105. 从前序与中序遍历序列构造二叉树

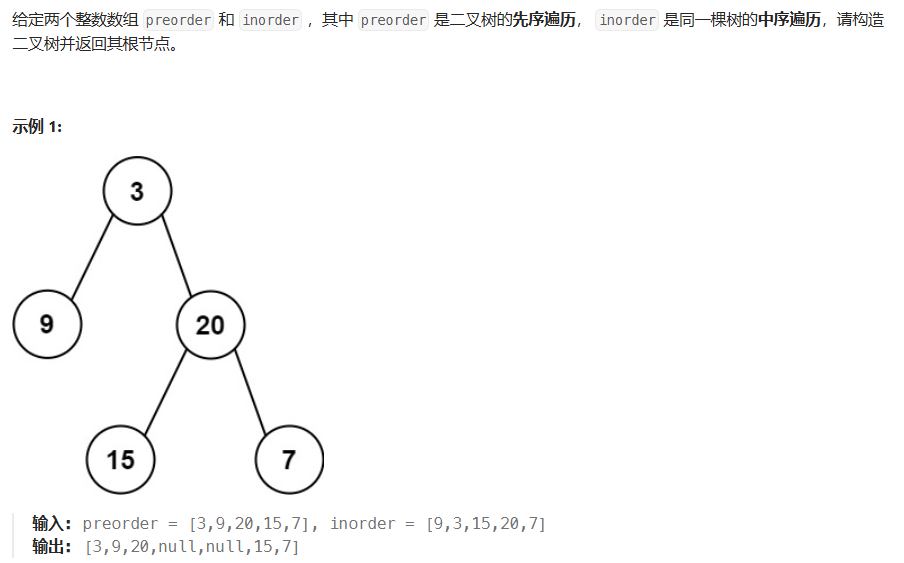
方法一：递归

方法二：迭代

102. 二叉树的层序遍历

方法一：bfs

98. 验证二叉搜索树

方法一：递归

方法二：中序遍历

96. 不同的二叉搜索树

方法一：dp

方法二：数学

78. 子集

方法一：迭代法

方法二：递归法

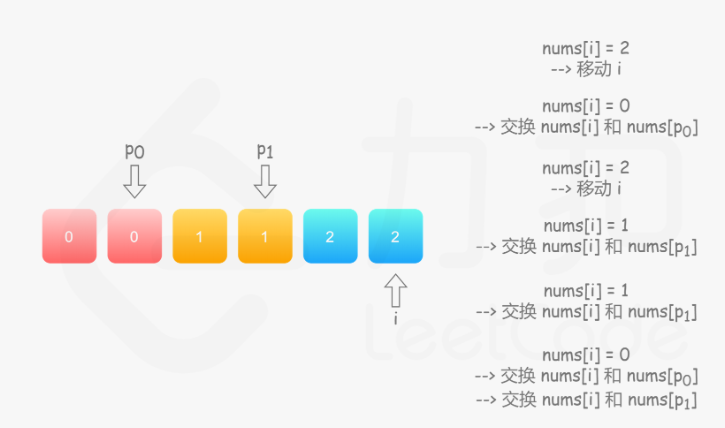
75. 颜色分类

方法一：统计法

统计出数组中 0,1,2 的个数，再根据它们的数量，重写整个数组

方法二：单指针

方法三：双指针1

方法四：双指针2

72. 编辑距离

方法一：dp

581. 最短无序连续子数组

方法一：排序

方法二：一次遍历

从左到右看，数应该越来越大，如果某个数，比前面最大值大，那他没问题，如果小于前面的最大值，那么这个数就有问题
从左到右不断更新最大值，遇到有问题的数，就记录下来作为right，并且right可以更新
right更新到最后面不动了，说明right右边的数都比right左边的max的数大，但是right自己比max小，right右边是排好序的，right左边需要重新排序，right是需要重新排序的区间的右边界。
left同理，left就是从右往左看，数要越来越小才行，如果某个数，比右边最小值还要小，那他没问题，如果它比右边的最小值要大，说明它有问题。

64. 最小路径和

方法一：dp

62. 不同路径

方法一：dp

如何理解滚动数组：对于那些只要求最终最佳答案的情况来说，通过用新的数据覆盖旧的数据来节省空间（降维）的一种策略。本题中随着外层的i++，就可以用f[j]+=f[j-1]来替换原来的f[i][j] = f[i - 1][j] + f[i][j - 1]

滚动数组（简单说明）_滚动数组思想-CSDN博客

方法二：组合数学

56. 合并区间

方法一：排序

Acwing_803（区间合并）-CSDN博客

55. 跳跃游戏

方法一：贪心

53. 最大子数组和

方法一：dp

这道题目的思想是：走完这一生如果我和你在一起会变得更好，那我们就在一起，否则我就丢下你。我回顾我最光辉的时刻就是和不同人在一起，变得更好的最长连续时刻

方法二：分治

困难（13道）：

124. 二叉树中的最大路径和

方法一：递归

核心是注意当前节点的最大路径，与当前节点作为子节点时的贡献是两个不同的值

当前节点的最大路径： max(自己，自己+左边，自己+右边，自己 + 左边 + 右边）
当前节点作为子节点时的贡献：max(自己，自己+左边，自己+右边）
后者相对前者，少了左右都存在的情况。因为作为子节点时，一条路如果同时包含左右，根就被包含了2次，不符合题目只出现一次的限制了。

312. 戳气球

方法一：记忆化搜索

注意这里的solve(i,j)中mid的选取是不断遍历得到的最优值，mid并非是区间内元素的最大值

方法二：dp

301. 删除无效的括号

前言：

方法一：回溯＋剪枝

用样例一举个例子：

方法二：bfs

方法三：枚举状态子集

297. 二叉树的序列化与反序列化

方法一：dfs

方法二：LL(1)型文法

239. 滑动窗口最大值

方法一：优先队列（堆）

方法二：单调队列

42. 接雨水

方法一：dp

方法二：单调栈

方法三：双指针

32. 最长有效括号

方法一：dp

方法二：栈

方法三：双计数器

方法四：栈模拟＋标记数组

23. 合并 K 个升序链表

方法一：顺序合并

方法二：分治合并

方法三：优先队列

10. 正则表达式匹配

方法一：dp

4. 寻找两个正序数组的中位数

方法一：二分查找

例子：

方法二：划分数组

时间复杂度：O(logmin(m,n)))

85. 最大矩形

方法一：使用柱形图的优化暴力做法

方法二：单调栈

84. 柱状图中最大的矩形

暴力做法：

方法一：单调栈

首先单调栈的经典应用场景是，在一维数组中，对每一个数字，找到前/后面第一个比自己大/小的元素。

该题的思路是：

对数组中的每个元素，若假定以它为高，能够展开的宽度越宽，那么以它为高的矩形面积就越大。
因此，思路就是找到每个元素左边第一个比它矮的矩形和右边第一个比它矮的矩形，在这中间的就是最大宽度
最后对每个元素遍历一遍找到最大值即可。

方法二：方法一优化