【剑指offer】面试题24：二叉搜索树的后序遍历序列

题目描述：

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

输入：

每个测试案例包括2行：

第一行为1个整数n(1<=n<=10000)，表示数组的长度。

第二行包含n个整数，表示这个数组，数组中的数的范围是[0,100000000]。

输出：

对应每个测试案例，如果输入数组是某二叉搜索树的后序遍历的结果输出Yes，否则输出No。

样例输入：

7

5 7 6 9 11 10 8

4

7 4 6 5

样例输出：

Yes

No

题目解析：

首先要看懂题目的意思，判断一个序列，是不是某一个二叉搜索树的后序遍历序列。也就是说，按照这个后序遍历的序列，能否构成一颗二叉搜索树！（也可以这样出题的）。

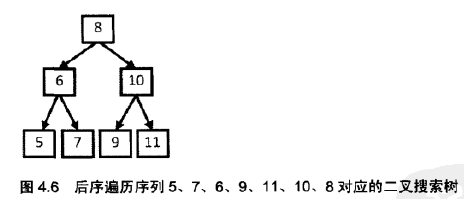
我们该如何下手呢？看到这个题目，一时找不到合适的思路。那么我们先画出一个二叉搜索树，看看他的后序遍历是什么：

不妨多花几个图。后序遍历的特点是父节点比子节点遍历晚，那么最晚遍历的也就是根结点了。所以我们可以看到最后一个数据8一定是根结点的数据。然后结合搜索树的特性，左结点<根<右子树，可以将剩余的结点划分成两部分，找到第一个大于根结点的位置即可划分。剩下的就是递归遍历了。

那么什么情况下不成立呢？也就是当找到第一个大于根结点的位置的时候，从该位置起到根结点，存在比根结点小的数据，那么显然不符合搜索树的定义。

根据这个思路得到如下完整代码：

#include <stdio.h>
#include <stdlib.h>

int JudegeBST(int arr[],int begin,int end);

int main()
{
    int n;
    int *buf;

    printf("input how many numbers you want to input :");
    while(scanf("%d",&n) == 1){
        buf = (int *)malloc(n * sizeof(int));

        printf("input the numbers:");
        for(int i = 0;i < n;++i)
            scanf("%d",&buf[i]);
        int result = JudegeBST(buf,0,n-1);
        if(result)
            printf("true!\n");
        else
            printf("false!\n");
    }
    return 0;
}

int JudegeBST(int arr[],int begin,int end)
{
    int i,result;

    if(begin >= end)
        return 1;

    for(i = begin;i < end;++i){ //寻找到第一个大于“根节点”的点
        if(arr[i] > arr[end])
            break;
    }
    for(int j = i;j < end;++j){     //判断后面的数据是否都大于“根节点”，如果不是，就返回0，表示不能构建二叉搜索树
        if(arr[j] < arr[end])
            return 0;
    }

    result = JudegeBST(arr,begin,i-1);
    if(!result)
        return 0;
    result = JudegeBST(arr,i,end-1);
    if(!result)
        return 0;
    return 1;
}

总结：

如果输入一个数组，让判断是不是某二叉搜索树的前序遍历呢？同样的方法，先找到根结点的位置，然后依据树的特性，将数组划分两部分。

那么我们可以总结出如下方法：

要求处理一棵二叉树的遍历序列，可以先找到根结点的位置，再基于根结点把整棵树拆分成左右子树序列，然后递归处理即可。面试题6“重建二叉树”也是利用的这个思想。