支配树 与 tarjan算法

简介

什么是支配树？支配树是什么？XD
对于一张有向图（可以有环）我们规定一个起点r（为什么是r呢？因为网上都是这么规定的），从r点到图上另一个点w可能存在很多条路径（下面将r到w简写为r->w）。
如果对于r->w的任意一条路径中都存在一个点p，那么我们称点p为w的支配点（当然这也是r->w的必经点），注意r点不讨论支配点。下面用idom[u]表示离点u最近的支配点。
对于原图上除r外每一个点u，从idom[u]向u建一条边，最后我们可以得到一个以r为根的树。这个树我们就叫它“支配树”。

---

相似

这个东西看上去有点眼熟？
支配点和割点（删掉后图联通块数增加）有什么区别？
我们考虑问题给定一个起点r和一个终点t，询问删掉哪个点能够使r无法到达t。
很显然，我们删掉任意一个r->t的必经点就能使r无法到达t，删掉任意一个非必经点，r仍可到达t。
从支配树的角度来说，我们只需删掉支配树上r到t路径上的任意一点即可
从割点的角度来说，我们是不是只需要考虑所有割点，判断哪些割点在r->t的路径上即可？是否将某个割点删掉即可让r无法到达t？
这当然是不正确的，我们可以从两个方面来说明它的错误：

1. 删掉割点不一定使r无法到达t
   
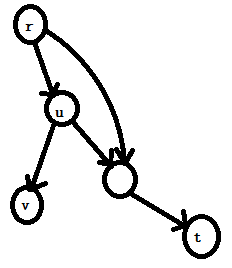
   这个图中点u是关键点（删掉后图联通块个数增加）
   并且u在r->t的路径上，然而删掉点u后r仍然可以到达t
2. 图中不一定存在割点
   
   在这个图中不存在任何割点

所以我们没有办法使用割点来解决这个问题。

---

简化问题

• 树

  对于一棵树，我们用r表示根节点，u表示树上的某个非根节点。很容易发现从r->u路径上的所有点都是支配点，而idom[u]就是u的父节点。
  这个可以在$O(n)$的时间内实现。

• DAG（有向无环图）

  因为是有向无环图，所以我们可以按照拓扑序构建支配树。
  假设当前我们构造到拓扑序中第x个节点编号为u，那么拓扑序中第1 ~ X-1个节点已经处理好了，考虑所有能够直接到达点u的节点，对于这些节点我们求出它们在支配树上的最近公共祖先v，这个点v就是点u在支配树上的父亲。
  如果使用倍增求LCA，这个问题可以在$O((n+m)log_2n)$的时间内实现。

对于这两个问题我们能够很简便的求出支配树。

---

有向图

对于一个有向图，我们应该怎么办呢？

简单方法

我们可以考虑每次删掉一个点，判断哪些点无法从r到达。
假设删掉点u后点v无法到达，那么点u就是r->v的必经点（点u就是v的支配点）。
这个方法我们可以非常简单的在$O(nm)$的时间内实现。
其中$n$是点数，$m$是点数。

更快的方法

这里，我将介绍Lengauer-Tarjan算法。
这个算法能在很快的时间内求出支配树。
要介绍这个算法我们还需引入两个定理和一些概念

大概步骤

首先来介绍一些这个算法的大概步骤

1. 对图进行DFS（深度优先遍历）并求出搜索树和DFS序。这里我们用$dfn[x]$表示点$x$在dfs序中的位置。
2. 根据半必经点定理计算出所有的半必经点作为计算必经点的根据
3. 根据必经点定理修正我们的半必经点，求出支配点

半必经点

我们用idom[x]表示点x的最近支配点，用semi[x]表示点x的半必经点。
那什么是半必经点呢？

对于一个节点$Y$，存在某个点$X$能够通过一系列点$p_i$（不包含$X$和$Y$）到达点$Y$且$\forall i$ $dfn[i] > dfn[Y]$，我们就称$X$是