Gaussian Bounding Boxes and Probabilistic Intersection-over-Union for Object Detection阅读笔记

(一) Title

论文:https://arxiv.org/abs/2106.06072
代码:https://github.com/ProbIOU

(二) Summary

研究背景:

目前目标检测算法基本上是通过bounding boxes来编码和表示object的形状和形状的,也就是有边界框的长宽和中心点坐标,general focal loss中也提到过在GT标注时实际上我们的GT并不是理论上的GT,而是认为标注的,有的时候物体的边界不好确定下来,对于模型来说,通过这种方式最多能够学习到一种带有置信度的标注,也就是对预测结果的确信程度。

本文方法：

本文中通过使用Gaussian分布来对目标区域进行模糊表示(fuzzy representation),相当于使用椭圆来表示边界框.接着本文针对高斯分布提出了一个基于Hellinger Distance的相似度度量,可以看成是Probabilistic Intersection-over-Union(ProbIoU),ProbIoU损失函数的优势在于：

• ProbIoU对于尺度缩放是不变的,不会随着尺度的变化导致损失值发生改变。
  目前该方法存在的问题是:对于方形w=h目标没有办法给出角度信息。

实验结果:

本文提出的Gaussian representations更加接近annotated segmentation,并且ProbIoU可以处理Gaussian representations的回归问题,ProbIoU能够很方便地添加到object detector中。

(三) Research Object

边界框的表示方式

• HBB,水平边界框,通过4个参数就能够表示,对于大型数据集来说标注比较友好。但是存在的问题是边界框包围的内容中包含了一部分背景,特别是对于拉长和旋转目标来说。
• 二进制Mask表示,通过mask来表示对象,标注时间较长,能够更加精细地表示对象。而且最后需要对应到原图大小上,模型架构比较复杂。
• OBB,旋转边界框,在RoI Transformer(不是Transformer encorder & decorder,仅仅表示一种变换)中将horizontal RoI变换成了OBB RoI,输出带有角度的proposals。

定位损失

• HBB边界框通常使用参数化损失parameter-wise loss components(比如说$l_1$和$l_2$正则,或者smooth $l1$),由于参数化损失隐式地假设每一个参数之间都是独立的,也就是一个参数的改变并不会影响另一个参数,因此参数化的损失might not converge consistently to the ground-truth(GT) annotation,
• 基于IoU的损失,IoU loss,GIoU,DIoU,CIoU,PIoU以及GWD

本文探索通过Gaussian Bounding Boxes(GBBs)来编码目标的representations，通过对目标使用GBBs的表示方式,并引入了一个可微分的损失来回归旋转框的参数或者直接回归GBB的参数(mean vector以及协方差矩阵covariance matrix).

(四) Problem Statement

本文提出使用Gaussian Bounding Boxes来表示目标,怎样得到目标的Gaussian Bounding Boxes表示呢？怎样回归边界框呢？

(五) Method

本文的核心思想就是:通过rotated Gaussian distribution来表示object,高斯分布可以参数化成均值向量$\mu ={\left(x_0,y_0\right)}^T$以及协方差矩阵$\Sigma$,构成了一个椭圆,也就相当于使用椭圆来对二维区域进行表示。

• 目标检测的工作实际上是基于预测框和真实框之间的距离差异构建损失函数进行回归,同样在这里也是这样,因为使用了高斯分布来表示目标,所以这里首先需要定义两个分布之间的距离.这个需要探索大量的统计工具来衡量.
• 高斯分布的形式带来了这些度量形式的closed-form differentiable表示,比如Bhatacharyya distance以及Kullback-Leibler divergence.为什么说高斯分布的形式对于这些度量能够可微呢？还是Kullback-Leibler divergence我之前记得貌似是不满足三角不等式的呀！

5.1 如何使用高斯分布来表示边界框

二维高斯分布的均值向量$\mathbf{\mu }={\left(x_0,y_0\right)}^T$,协方差矩阵$\Sigma$,协方差矩阵具有两种表示方式：
$$\Sigma =\left[\begin{array}{ll}a& c\\ c& b\end{array}\right]=R_{\theta }\left[\begin{array}{cc}{a}^{\prime }& 0\\ 0& b^{\prime }\end{array}\right]R_{\theta }^T=\left[\begin{array}{cc}{a}^{\prime }{\cos }^2\theta +b^{\prime }{\sin }^2\theta & \frac{1}{2}\left(a^{\prime }-b^{\prime }\right)\sin 2\theta \\ \frac{1}{2}\left(a^{\prime }-b^{\prime }\right)\sin 2\theta & a^{\prime }{\sin }^2\theta +b^{\prime }{\cos }^2\theta \end{array}\right]$$
第一种表示方式一个对称的协方差矩阵,从埃尔米特矩阵的定义来看(矩阵中每一个第i行第j列的元素与第j行第i列的元素的共轭相同)，协方差矩阵就是埃尔米特矩阵

根据埃尔米特矩阵的性质可知:如果埃尔米特矩阵的特征值都是正数,那么这个矩阵就是正定矩阵,如果他们是非负的,那这个矩阵就是半正定矩阵。

从上面的性质可知,$a>0,ab-c^2>0,b>0$.

第二种表示方式是使用旋转矩阵进行表示。其中旋转矩阵的表示方式为,给定坐标$(x_1,y_1)$,绕坐标$(0,0)$顺时针旋转$\theta$角度后得到坐标$(x,y)$,计算方式如下：
$$\left[\begin{array}{l}x\\ y\end{array}\right]=\left[\begin{array}{l}{x}_{1}cos\theta -y_{1}sin\theta \\ y_{1}cos\theta +x_{1}sin\theta \end{array}\right]=\left[\begin{array}{ll}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\left[\begin{array}{l}{x}_1\\ y_1\end{array}\right]=R_{\theta }\left[\begin{array}{l}{x}_1\\ y_1\end{array}\right]$$

因此从上面两种表示方式来看,为了得到协方差矩阵可以直接回归$(a,b,c)$或者回归$(a^{\prime },b^{\prime },\theta )$,对于旋转边界框来说,使用$(a^{\prime },b^{\prime },\theta )$表示是很合适的,而$(a^{\prime },b^{\prime },\theta )$和$(b^{\prime },a^{\prime },\theta +\frac{\pi }{2})$表示的都是相同的协方差矩阵,为了$(a^{\prime },b^{\prime },\theta )$形式下能够有一个独一无二表示方式,这里限制$\theta \in [-\frac{\pi }{4},\frac{\pi }{4}]$,当$a^{\prime }=b^{\prime }$时,表示的是各项同性的高斯核,此时角度$\theta$取任何值都对应着相同的协方差矩阵。对于方形的矩形框来说,旋转边界框仍然对应着一个角度,然而GBB的表示方式给出的角度却可以是任意的，从而导致了从OBB表示变换成GBB是不可逆的,会存在角度信息的丢失

作者是怎么想到从边界框表示的角度来引入GBB呢？感觉很妙啊,想法很妙,然后接下来的问题是现有的对目标的OBB,HBB以及mask表示中得到目标GBB的表示呢？

• 获取GBB的关键就是得到均值向量和协方差矩阵。首先假设目标区域使用一个2D的binary区域来进行表示，这个区域又是一个概率密度函数(PDF),均值和方差可以通过对区域进行积分进行表示：
  $$\mathbf{\mu }=\frac{1}{N}{\int }_{\mathbf{x}\in \Omega }\mathbf{x},\Sigma =\frac{1}{N}{\int }_{\mathbf{x}\in \Omega }(\mathbf{x}-\mathbf{\mu })(\mathbf{x}-\mathbf{\mu }{)}^T$$
  实际上连续函数的均值和方差的计算方式表示为：
  $$\begin{gathered} \mathrm{E}(X)={\int }_{-\infty }^{\infty }xf(x)\mathrm{d}x \\ \mathrm{Var}(X)={\sigma }^2=\int (x-\mu {)}^{2}f(x)dx \end{gathered}$$
  因此可以得知,均值和协方差计算中的$\frac{1}{N}$对应着概率密度函数(PDF),其中$N$表示区域$\Omega$的面积。
• 对于水平框HBB来说,区域$\Omega$是一个矩形,中心点位置为$(x_0,y_0)$,宽为$W$,高为$H$,计算出来的均值向量和协方差矩阵为：
  $$\begin{gathered} \mathbf{\mu }=(x_0,y_0{)}^T \\ \Sigma =\frac{1}{WH}{\int }_{-H/2}^{H/2}{\int }_{-W/2}^{W/2}\left[\begin{array}{ll}{x}^2& xy\\ xy& y^2\end{array}\right]dxdy=\frac{1}{12}\left[\begin{array}{cc}{W}^2& 0\\ 0& H^2\end{array}\right] \end{gathered}$$
  对应着第一种表示方式中的协方差矩阵$\left[\begin{array}{ll}a& c\\ c& b\end{array}\right]$,也就是$a=\frac{W^2}{12}$,$b=\frac{H^2}{12}$,$c=0$,对于旋转框来说,首先计算不相关的方差$a^{\prime },b^{\prime }$,需要同时计算角度$\theta$,对应的协方差矩阵$\Sigma$可以使用$R_{\theta }\left[\begin{array}{cc}{a}^{\prime }& 0\\ 0& b^{\prime }\end{array}\right]R_{\theta }^T$表示,如果目标的表示方式是使用参数化的2D形状(多边形)，可以通过均值和协方差的计算公式得到高斯分布的均值和方差，如果是目标的表示方式是使用binary分割的mask来表示,采用离散方式计算均值和方差。
  如果说最后我们希望输出边界框的中心点和长宽,也可以利用计算出来的均值向量和协方差矩阵反推出来矩形框的中心点和尺寸。
• 关于多元高斯分布的一些补充内容为:
  马氏平方距离$d^2(\mathbf{x})=(\mathbf{x}-\mathbf{\mu }{)}^T{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })$表示一个卡方分布(带有两个方向的自由度)，然后设置$d^2(\mathbf{x})=r^2$(其中$r$大于0表示椭圆区域)。考虑HBB情况下对应的方程为:
  $$d^2(\mathbf{x})=(\mathbf{x}-\mathbf{\mu }{)}^T{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })=(x-x_0{)}^2{\lambda }_1+(y-y_0{)}^2{\lambda }_2=r^2$$
  椭圆的表示方程为：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,对应到上面的表示,此时椭圆的semi-axes分别为$r/\sqrt{{\lambda }_1}$和$r/\sqrt{{\lambda }_2}$,其中${\lambda }_1$和${\lambda }_2$是${\Sigma }^{-1}$的特征向量,对于旋转框来说,仅仅是椭圆的主方向换成了${\Sigma }^{-1}$的特征向量方向,其他的方向并没有发生改变,因此这里还可以变化的是$r$(这里应该是另一种解释方式,还没有对$r$进行约束),然后给定一个面积阈值$0<\tau <1$,可以设置$r$满足$F_{{\chi }^2}\left(r^2\right)=\tau$,其中$F_{{\chi }^2}$表示卡方分布的累积分布函数(CDF),如果GBB用来计算水平框或者旋转框时,需要生成一个和
  $$\begin{gathered} \mathbf{\mu }=(x_0,y_0{)}^T \\ \Sigma =\frac{1}{WH}{\int }_{-H/2}^{H/2}{\int }_{-W/2}^{W/2}\left[\begin{array}{ll}{x}^2& xy\\ xy& y^2\end{array}\right]dxdy=\frac{1}{12}\left[\begin{array}{cc}{W}^2& 0\\ 0& H^2\end{array}\right] \end{gathered}$$
  面积完全相同的椭圆,此时需要设置$r=\sqrt{12/\pi }$,然后对应着的$\tau \approx 0.85$,这里需要解释的包括：卡方分布的CDF以及为什么设置$r=\sqrt{12/\pi }$？卡方分布的CDF有什么含义呢？这里还是不理解,为什么是这样呢？

5.2 ProbIoU以及定位损失

给定了GTannotation以及Pred的GBBs表示方式,首先需要定义的是怎么计算两个GBB之间的相似性,本文中考虑的是 Bhattacharyya Coefficient/Distance(巴氏系数/巴氏距离,注意巴氏系数和巴氏距离不是一个东西)可以用来作为一个实际的距离度量。

两个概率密度函数$p(\mathbf{x})$和$q(\mathbf{x})$之间的Bhattacharyya Coefficient定义如下：
$$B_C(p,q)={\int }_{{\mathbb{R}}^2}\sqrt{p(\mathbf{x})q(\mathbf{x})}d\mathbf{x}$$
用来度量两个分布overlap的程度,$B_C(p,q)\in [0,1]$,并且当且仅当两个分布完全相同时,才有$B_C(p,q)=1$,而巴氏距离度量两个分布的相似程度,巴氏距离的定义为：
$$B_D(p,q)=-\ln B_C(p,q)$$

对于本文来说,两个分布为高斯分布,即$p\sim \mathcal{N}\left({\mathbf{\mu }}_1,{\Sigma }_1\right)$以及$q\sim \mathcal{N}\left({\mathbf{\mu }}_2,{\Sigma }_2\right)$,并且给出下列表示：
$${\mathbf{\mu }}_1=\left(\begin{array}{l}{x}_1\\ y_1\end{array}\right),{\Sigma }_1=\left[\begin{array}{ll}{a}_1& c_1\\ c_1& b_1\end{array}\right],{\mathbf{\mu }}_2=\left(\begin{array}{l}{x}_2\\ y_2\end{array}\right),{\Sigma }_2=\left[\begin{array}{ll}{a}_2& c_2\\ c_2& b_2\end{array}\right]$$
从而能够得到$B_D$的close-form表示为：
$$B_D=\frac{1}{8}{\left({\mathbf{\mu }}_1-{\mathbf{\mu }}_2\right)}^T{\Sigma }^{-1}\left({\mathbf{\mu }}_1-{\mathbf{\mu }}_2\right)+\frac{1}{2}\ln \left(\frac{\det \Sigma }{\sqrt{\det {\Sigma }_1\det {\Sigma }_2}}\right),\Sigma =\frac{1}{2}\left({\Sigma }_1+{\Sigma }_2\right)$$
多维正态分布的概率密度函数为：
$$f_{\mathrm{x}}\left(x_1,\dots ,x_k\right)=\frac{1}{\sqrt{(2\pi {)}^k|\Sigma |}}{\mathrm{e}}^{-\frac{1}{2}(\mathrm{x}-\mu {)}^{\mathrm{T}}{\Sigma }^{-1}(\mathrm{x}-\mu )}$$
然后按照上面的公式计算$B_D$得到的是：
$$B_D=\frac{1}{8}{\left({\mathbf{\mu }}_1-{\mathbf{\mu }}_2\right)}^T{\Sigma }^{-1}\left({\mathbf{\mu }}_1-{\mathbf{\mu }}_2\right)+\frac{1}{2}\ln \left(\frac{\det \Sigma }{\sqrt{\det {\Sigma }_1\det {\Sigma }_2}}\right),\Sigma =\frac{1}{2}\left({\Sigma }_1+{\Sigma }_2\right)$$
接着将$B_D$拆开,分成$B_1$和$B_2$，然后将$p$和$q$分布的参数带入到$B_D$中得到了：
$$\begin{array}{c}{B}_1=\frac{1}{4}\frac{\left(a_1+a_2\right){\left(y_1-y_2\right)}^2+\left(b_1+b_2\right){\left(x_1-x_2\right)}^2+2\left(c_1+c_2\right)\left(x_2-x_1\right)\left(y_1-y_2\right)}{\left(a_1+a_2\right)\left(b_1+b_2\right)-{\left(c_1+c_2\right)}^2},\\ B_2=\frac{1}{2}\ln \left(\frac{\left(a_1+a_2\right)\left(b_1+b_2\right)-{\left(c_1+c_2\right)}^2}{4\sqrt{\left(a_1{b}_1-c_1^2\right)\left(a_2{b}_2-c_2^2\right)}}\right),\end{array}$$
$B_D=B_1+B_2$,因此,$B_C$的close-form表示为$B_C=e^{-B_D}$,并且$B_2$仅仅跟协方差矩阵参数相关，而跟均值参数无关,因此,中心点和形状可以分别考虑,然后$B_1$和$B_2$可以增加不同的系数进行来进行不同的考虑。然而巴氏距离并不满足三角不等式,使用Hellinger distance(海林格距离)可以满足距离度量
$$H_D(p,q)=\sqrt{1-B_c(p,q)}$$
并且可以表示成高斯分布参数的函数,并且$0\le H_D(p,q)\le 1$,对于高斯分布来说,总是有$H_D(p,q)>0$,当$p\ne q$时，并且由于高斯分布是无穷的,因此$B_C(p,q)$总是严格正的。在本文中提出使用$1-H_D(p,q)$来表示两个高斯分布之间的相似性，并记作ProbIoU,解决了GWD中的一些问题.
本文中给定预测边界框$\mathbf{p}=\left(x_1,y_1,a_1,b_1,c_1\right)$和真实边界框$\mathbf{q}=\left(x_2,y_2,a_2,b_2,c_2\right)$之间的基于ProbIoU的损失函数为:
$$\begin{gathered} {\mathcal{L}}_1(\mathbf{p},\mathbf{q})=H_D(\mathbf{p},\mathbf{q})=1-\mathrm{ProbIoU}(\mathbf{p},\mathbf{q})\in [0,1], \\ {\mathcal{L}}_2(\mathbf{p},\mathbf{q})=B_D(\mathbf{p},\mathbf{q})=-\ln \left(1-{\mathcal{L}}_1^2(\mathbf{p},\mathbf{q})\right)\in [0,\infty ], \end{gathered}$$
上面有两个基于ProbIoU的损失函数,首先第一个损失${\mathcal{L}}_1(\mathbf{p},\mathbf{q})$当GBBs之间相距很远时,${\mathcal{L}}_1(\mathbf{p},\mathbf{q})$的值非常接近1,产生的梯度值非常小,导致收敛很慢。${\mathcal{L}}_2(\mathbf{p},\mathbf{q})$并不存在这个问题,不过不能很好地表示和IoU之间的关系。当前的训练方式为：首先采用${\mathcal{L}}_2(\mathbf{p},\mathbf{q})$进行训练,然后再采用${\mathcal{L}}_1(\mathbf{p},\mathbf{q})$进行训练
对于HBB边界框时:

• 协方差矩阵中的$c$变成了0,然后对于协方差矩阵的要求变成了$a>0,b>0$
• 对于HBB边界框参数${\mathbf{p}}_B=\left(x_1,y_1,W_1,H_1\right)$,基于之前提到的计算均值和协方差矩阵的方式能够得到GBB的表示方式${\mathbf{p}}_G=\left(x_1,y_1,a_1,b_1\right)=\mathbf{f}\left({\mathbf{p}}_B\right)=\left(x_1,y_1,W_1^2/12,H_1^2/12\right)$，同样对于GT边界框进行相同的变换得到${\mathbf{q}}_G=\left(x_2,y_2,a_2,b_2\right)=\mathbf{f}\left({\mathbf{q}}_B\right)=\left(x_2,y_2,W_2^2/12,H_2^2/12\right)$,
• 上面提到的两个损失中包含的$B_D(p,q)$项对于旋转框就可以简化成:
  $$B_D\left({\mathbf{p}}_G,{\mathbf{q}}_G\right)=\frac{1}{4}\left(\frac{{\left(x_1-x_2\right)}^2}{a_1+a_2}+\frac{{\left(y_1-y_2\right)}^2}{b_1+b_2}\right)+\frac{1}{2}\ln \left(\left(a_1+a_2\right)\left(b_1+b_2\right)\right)-\frac{1}{4}\ln \left(a_1{a}_2{b}_1{b}_2\right)$$
  当使用上面的损失函数进行梯度反向传播时,需要计算$\partial B_D/\partial {\mathbf{p}}_G$，并且有$\partial B_D/\partial {\mathbf{p}}_G=0\iff {\mathbf{p}}_G={\mathbf{q}}_G\iff {\mathbf{p}}_B={\mathbf{q}}_B$，

没有弄明白为什么when ${\mathcal{L}}_2$用于localization loss时不能出现梯度消失呢？关于收敛慢的原因由于${\mathcal{L}}_1=\sqrt{1-\exp \left(-B_D\right)}$导致梯度计算中存在指数项,当预测边界框和真实边界框相差很远时,此时$B_C(p,q)\approx 0,B_D(p,q)\to \inf$,从而指数项的梯度值很小，通过${\mathcal{L}}_2$引入指数函数倒数将指数项去掉来进行收敛。因此这里采用的是two-stage training protocol首先采用${\mathcal{L}}_2$先训练一会，然后再 切换到${\mathcal{L}}_1$进行训练,那么什么时候是最佳的切换时机呢？

(六) Experiments

训练中的设置,仅仅替换掉损失函数,其他的保持相同,对于两种loss切换的设置为:使用$L_2$损失训练总epoch数的一半,剩下的一半切换到$L_1$,并且$L_1$损失和$L_2$损失在同分类损失结合时，分别有$w_1$和$w_2$参数，在作者的实验中设置的是$w_2\approx 5w_1$,来保持从$L_2$切换到$L_1$时具有相同的梯度，因此这里设置了一个超参数$w$,令$w_1=w,w_2=5w$

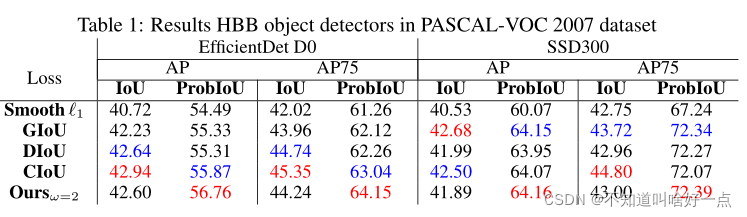
效果好的我都有点儿怀疑~,真的能够有这么大的提升嘛？


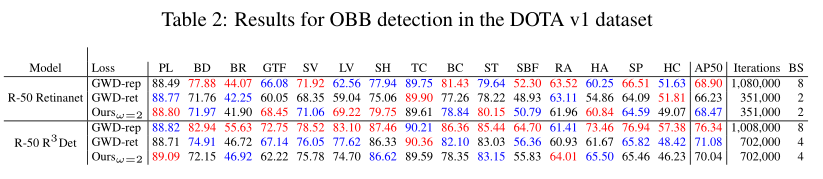
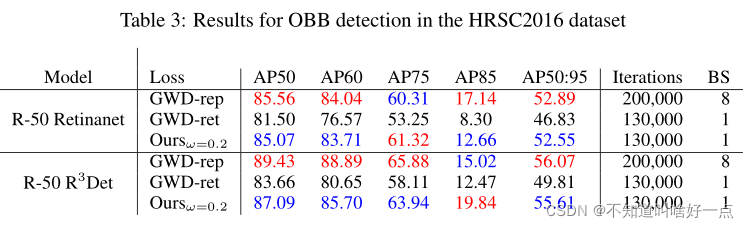
不过在旋转框中的表现效果看着并没有GWD出色啊~

(七) Conclusion

本文引入了对于目标描述的GBB表示,能够用在mask,HBB以及OBB任务上,并且提出了用于损失计算的ProbIoU。