Cayley公式及Prüfer编码详解

介绍

$Cayley$ 公式是用来求这样一个问题的：问 $n$ 个有标号点能组成多少棵不同的树。

注意：有标号意味着每个点之间是不同的。

而 $Pr\ddot{u}fer$ 编码是一种对无根树的编码方式，它可以保证每一棵无根树都对应唯一一个 $Pr\ddot{u}fer$ 编码，而每一个 $Pr\ddot{u}fer$ 编码都对应唯一一棵无根树。

$Cayley$ 公式

公式很好记，长这个样子：$n^{n-2}。$

怎么证明呢？得先讲讲 $Pr\ddot{u}fer$ 编码是个啥。

$Pr\ddot{u}fer$ 编码

对于一棵点有标号的无根树，编码的规则是这样的：每次找到叶子结点中编号最小的，将与它相邻的点记下，然后删掉它，重复该操作，直到只剩两个节点。

为什么是两个节点呢而不是一个呢？下面再讲qwq。

模拟一下吧，比如说一开始有这样一棵树：

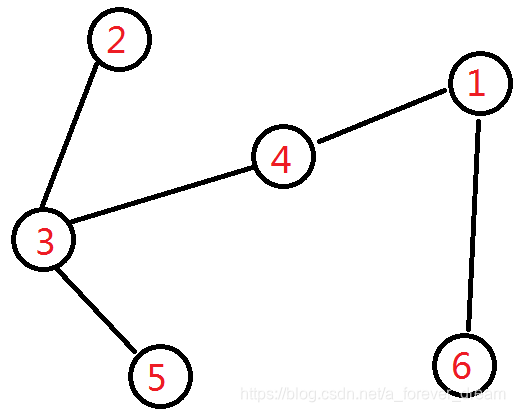
此时叶子结点有：$2,5,6$ 。

编号最小的是 $2$，与它相邻的节点是 $3$，将他记下，然后将 $2$ 删掉。

此时的 $Pr\ddot{u}fer$ 编码为：$3$。

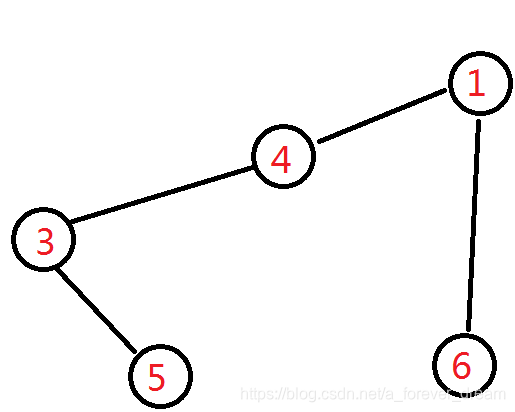
此时的叶子结点有： $5,6$。

编号最小的是 $5$，与它相邻的节点是 $3$，将他记下，然后将 $5$ 删掉。

此时的 $Pr\ddot{u}fer$ 编码为：$3,3$。

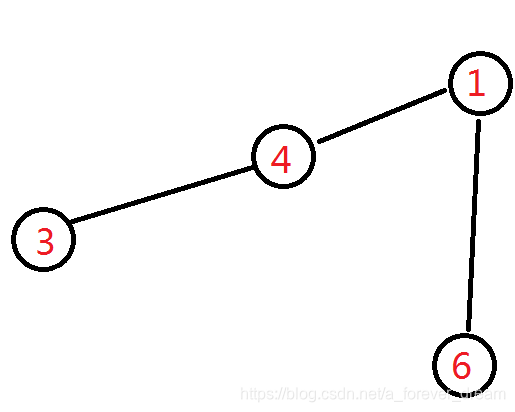
此时的叶子结点有： $3,6$。

编号最小的是 $3$，与它相邻的节点是 $4$，将他记下，然后将 $3$ 删掉。

此时的 $Pr\ddot{u}fer$ 编码为：$3,3,4$。

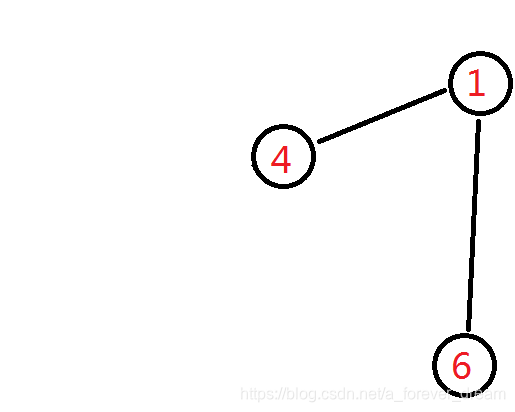
此时的叶子结点有： $4,6$。

编号最小的是 $4$，与它相邻的节点是 $1$，将他记下，然后将 $4$ 删掉。

此时的 $Pr\ddot{u}fer$ 编码为：$3,3,4,1$。

此时只剩两个节点，于是我们就愉快地做完了！

那么，原树的 $Pr\ddot{u}fer$ 编码就是：$3,3,4,1$。

---

显然，每一棵树都对应着恰好一个 $Pr\ddot{u}fer$ 编码，下面只需证明每一个 $Pr\ddot{u}fer$ 编码都对应着恰好一棵树。

证明

证明也很简单，我们上面是在模拟找一棵树的 $Pr\ddot{u}fer$ 编码，我们可以用类似的方法模拟找一棵 $Pr\ddot{u}fer$ 编码对应的树。

首先有这样一个性质：没有出现在 $Pr\ddot{u}fer$ 编码里的数字，都是原树里的叶子结点。比如说上面那个例子里，原树的叶子结点有：$2,5,6$，都没有出现在这棵树的 $Pr\ddot{u}fer$ 编码里。

模拟：

于是考虑 $Pr\ddot{u}fer$ 编码的第一位：这个数一定与原树的叶子结点中编号最小的那个有连边，于是我们给它们两个之间连上一条边。然后将这个数从 $Pr\ddot{u}fer$ 编码中删去。

然后考虑 $Pr\ddot{u}fer$ 编码的第二位：这个数一定与此时不在 $Pr\ddot{u}fer$ 编码中且没有处理过的最小的数之间有连边，我们给它们连上边，然后将 $Pr\ddot{u}fer$ 编码的第二位删掉。（我们称 没有被当做过编号最小的数 为 没有被处理过的。）

……

我们一直重复上面的过程，就可以连出 $n-2$ 条边，而最后一条边连剩下的两个没处理的节点即可。

那么显然，一个 $Pr\ddot{u}fer$ 编码也对应着恰好一棵树。

那么这里发现一个性质：我们连完 $n-2$ 条边之后，最后一条边连的两个对象是固定的。

这就解释了 $Pr\ddot{u}fer$ 编码为什么在 $2$ 个节点的时候就停下，因为没有必要再往下编一位了，假如前面的 $n-2$ 位已经知道，那么第 $n-1$ 位其实是固定的。

假如去掉这多余的 $1$ 位，那么反而还能更方便求解。

回到 $Pr\ddot{u}fer$ 编码

那么为什么有这样一条柿子呢？

我们发现，一个 $n-2$ 位的编码可以对应一棵 $n$ 个点的树，并且这个编码没有特殊限制，那么要求一棵 $n$ 个点的树有多少种形态，就相当于要求一个长度为 $n-2$ 的序列有多少种填法，其中每一位可以填 $[1,n]$ 中的某一个数。

那么显然答案就是 $n^{n-2}$ 了。

应用

例题1

掏一道例题出来：父子。

求 $n$ 个点的有根树形态数。

显然就是一个模板题了，无根树转有根树，我们只需要将 $[1,n]$ 中的某个点当做根即可，那么让答案乘以 $n$ 即可。也就是 $n^{n-1}$。

代码就不必了吧。

例题2

求 $n$ 个点形成的 $m$ 棵树组成的有根森林的方案数。

有根是个很不错的条件，考虑一个虚点 $0$ 连向 $m$ 棵树的根，并强制令 $0$ 的度为 m。

那么在 $Pr\ddot{u}fer$ 编码中，$0$ 需要出现恰好 $m-1$ 次，即 $\left(\genfrac{}{}{0ex}{}{n-1}{m-1}\right)$。

剩下的位置随便填（但不能是 $0$），即 $n^{n-m-1}$。两部分乘起来就是答案。

例题3

HNOI 2004 树的计数

这题我们依然考虑 $Pr\ddot{u}fer$ 编码，他给出了每个点的度为 $d[i]$，那么这个点在编码中的出现次数就是 $d[i]-1$，那么问题转化成：有一个长度为 $n-2$ 序列，其中数字 $i$ 的出现次数为 $d[i]-1$，问这个序列有多少种可能。

第一种表示   这个序列有 $(n-2)!$ 种排列，但是对于其中相同的数，他们无论怎么排列这个序列都是一样的，比如说 $i$ 这个数出现了 $d[i]-1$ 次，那么这个序列里面的 $d[i]-1$ 个 $i$ 无论怎么交换位置，这个序列都不会改变，所以答案要除以 $(d[i]-1)!$。

那么答案就是 $(n-2)!/[(d[1]-1)!(d[2]-1)!...(d[n]-1)!]$。

第二种表示   这种表示只是为了更好地理解。

因为 $1$ 这个数出现过 $d[1]-1$ 次，那么在 $n-2$ 个位置中放 $d[1]-1$ 个 $1$ 的方案数就是 $C_{n-2}^{d[1]-1}$。

第二个数的出现次数为 $d[2]-1$ 次，在剩下的 $n-2-d[1]+1$ 个位置中放 $d[2]-1$ 个 $2$ 的方案数为 $C_{n-2-d[1]+1}^{d[2]-1}$。

……

然后所有的组合数乘起来，化简后可以得到第一种表示。

代码在这里面。