引言
在科学计算中会遇到大量求解非线性方程的情况。如代数方程(二次、三次等),超越方程(三角方程,指数、对数方程等)。即便是基本的代数方程,当次数超过4次时,一般就不能用公式表示方程的根了。为了解决这些问题就要用到数值方法了。
简单迭代法
先将
f
(
x
)
=
0
f(x)=0
f(x)=0化为一个与它同解的方程
x
=
φ
(
x
)
x=\varphi(x)
x=φ(x),即如果数
α
\alpha
α使得
f
(
α
)
=
0
f(\alpha)=0
f(α)=0,则有
α
=
φ
(
α
)
\alpha=\varphi(\alpha)
α=φ(α),反之亦然。这样我们就可以构造一个迭代过程,来求出
α
\alpha
α的近似值。
任取初始值
x
0
x_0
x0,得
x
1
=
φ
(
x
0
)
x_1=\varphi(x_0)
x1=φ(x0),再把
x
1
x_1
x1带入,求得
x
2
=
φ
(
x
1
)
x_2=\varphi(x_1)
x2=φ(x1),继为之,便可得到一个数列。一般表示形式为
x
k
+
1
=
φ
(
x
k
)
(
k
=
0
,
1
,
2
,
.
.
.
)
x_{k+1}=\varphi(x_k)(k=0,1,2,...)
xk+1=φ(xk)(k=0,1,2,...)。这就是求解非线性方程的简单迭代法(迭代法、迭代过程、迭代格式),
φ
(
x
)
\varphi(x)
φ(x)为迭代函数,
x
k
x_k
xk称第k步的迭代值。
如果由迭代格式产生的数列收敛,即
lim
k
→
∞
x
k
=
α
\lim\limits_{k\to\infty}x_k=\alpha
k→∞limxk=α,则称迭代法收敛,否则称迭代法发散。若收敛,
α
\alpha
α就是方程的根
来看个例子:求
f
(
x
)
=
2
x
3
−
x
−
1
f(x)=2x^3-x-1
f(x)=2x3−x−1的根。用迭代法,我们化为等价方程
x
=
x
+
1
2
3
x=\sqrt[3]{\frac{x+1}{2}}
x=32x+1,则迭代公式为
x
k
+
1
=
x
k
+
1
2
3
x_{k+1}=\sqrt[3]{\frac{x_k+1}{2}}
xk+1=32xk+1。或者化为
x
=
2
x
3
−
1
x=2x^3-1
x=2x3−1,迭代格式:
x
k
+
1
=
2
x
k
3
−
1
x_{k+1}=2x_k^3-1
xk+1=2xk3−1,初始值都取
x
0
=
0
x_0=0
x0=0,计算后发现一个收敛一个发散。这说明,迭代法的收敛与发散,依赖于迭代函数
迭代函数构造的方法很多,例如
x
−
f
(
x
)
=
x
x-f(x)=x
x−f(x)=x,进一步
x
−
k
(
x
)
f
(
x
)
=
x
,
(
k
(
x
)
≠
0
)
x-k(x)f(x)=x,(k(x)\neq0)
x−k(x)f(x)=x,(k(x)=0)。那么迭代函数要满足什么条件,迭代法才收敛呢?从下图可以看出:

迭代函数满足
φ
′
(
x
)
<
1
\varphi^{'}(x)<1
φ′(x)<1时,迭代法收敛。
迭代终止条件与迭代次数
来看一个定理:设迭代函数
φ
(
x
)
\varphi(x)
φ(x)满足,1、当
x
∈
[
a
,
b
]
时
,
a
≤
φ
(
x
)
≤
b
x\in[a,b]时,a\leq\varphi(x)\leq b
x∈[a,b]时,a≤φ(x)≤b。2、存在正数
0
<
L
<
1
0<L<1
0<L<1,对任意
x
∈
[
a
,
b
]
均
有
∣
φ
′
(
x
)
∣
≤
L
x\in[a,b]均有|\varphi^{'}(x)|\leq L
x∈[a,b]均有∣φ′(x)∣≤L,则
x
=
φ
(
x
)
x=\varphi(x)
x=φ(x)在[a,b]内存在唯一根
α
\alpha
α,且对任意初始值
x
0
∈
[
a
,
b
]
x_0\in[a,b]
x0∈[a,b],迭代法收敛于
α
\alpha
α,且有:1式
∣
x
k
−
α
∣
≤
L
1
−
L
∣
x
k
−
x
k
−
1
∣
|x_k-\alpha|\leq \frac{L}{1-L}|x_k-x_{k-1}|
∣xk−α∣≤1−LL∣xk−xk−1∣以及2式
∣
x
k
−
α
∣
≤
L
k
1
−
L
∣
x
1
−
x
0
∣
|x_k-\alpha|\leq \frac{L^k}{1-L}|x_1-x_{0}|
∣xk−α∣≤1−LLk∣x1−x0∣
从这个定理来看,相邻两次计算值的偏差
∣
x
k
−
x
k
−
1
∣
|x_k-x_{k-1}|
∣xk−xk−1∣达到事先给定的精度要求,迭代过程就可以终止。由2式可以大概估计迭代过程所需要的迭代次数。但是由于定理的条件一般很难验证,也不一定成立。所以在根附近进行迭代。由2式可以看出,当L或
∣
φ
′
(
x
)
∣
|\varphi^{'}(x)|
∣φ′(x)∣在[a,b]上的值越小,迭代过程收敛速度就越快,当L<1且接近1时,收敛速度很慢。
收敛速度的阶
为了使收敛速度有定量的判断,引入收敛速度的阶概念。设迭代格式
x
k
+
1
=
φ
(
x
k
)
x_{k+1}=\varphi(x_k)
xk+1=φ(xk),当
k
→
∞
k\to\infty
k→∞时,
x
k
+
1
→
α
x_{k+1}\to\alpha
xk+1→α,并记
e
k
=
x
k
−
α
e_{k}=x_k-\alpha
ek=xk−α。
若存在实数
p
≥
1
,
c
>
0
满
足
lim
k
→
∞
∣
e
k
+
1
∣
∣
e
k
∣
p
=
c
p\geq1,c>0满足\lim\limits_{k\to\infty}\frac{|e_{k+1}|}{|e_k|^p}=c
p≥1,c>0满足k→∞lim∣ek∣p∣ek+1∣=c,则称迭代法是p阶收敛。
当p=1时,称为线性收敛;
当p>1时,称为超线性收敛;
当p=2时,称为平方收敛;
p越大迭代法收敛速度越快。
那p如何确定呢,有定理:
如果
x
=
φ
(
x
)
x=\varphi(x)
x=φ(x)中的迭代函数在根
α
\alpha
α附近满足:
(1)
φ
(
x
)
\varphi(x)
φ(x)存在p阶连续导函数
(2)
φ
′
(
α
)
=
φ
′
′
(
α
)
=
.
.
.
=
φ
p
−
1
(
α
)
=
0
,
φ
p
(
α
)
≠
0
\varphi^{'}(\alpha)=\varphi^{''}(\alpha)=...=\varphi^{p-1}(\alpha)=0,\varphi^{p}(\alpha)\neq0
φ′(α)=φ′′(α)=...=φp−1(α)=0,φp(α)=0则迭代法
x
k
+
1
=
φ
(
x
k
)
x_{k+1}=\varphi(x_k)
xk+1=φ(xk)是p阶收敛。
Newton迭代法及其变形
用迭代法求解非线性方程,构造迭代函数使其收敛非常重要。无论非线性方程f(x)=0形式如何,总有以下构造方法:
x
=
φ
(
x
)
=
x
−
k
(
x
)
f
(
x
)
,
(
k
(
x
)
≠
0
)
x=\varphi(x)=x-k(x)f(x),(k(x)\neq0)
x=φ(x)=x−k(x)f(x),(k(x)=0)
前面说过迭代函数的导数绝对值小于1则收敛,且越小收敛速度越快,我们令其导函数为0。有以下推算:

由此引出定理:
方程f(x)=0的根为
α
,
f
′
(
α
)
≠
0
\alpha,f^{'}(\alpha)\neq0
α,f′(α)=0则:

式4-26带有f(x)的导函数,使用不方便,用其近似值代替,有:

我们来看下它们的几何意义:



从图中也可看出,弦截法需要两个初值。
Newton法的收敛性与初始值的选取有很大关系(在根附近讨论,局部收敛性)。初始值选择不当,会导致发散,下面介绍一种大范围内收敛的方法。
一种大范围收敛的Newton型方法
为了防止迭代发散,我们符加一个条件:

其中的下山因子一般采用试算法。由迭代得到
x
k
x_k
xk后,取不同的
λ
\lambda
λ进行试算,例如:1,1/2,1/4,1/8…。计算出
x
k
+
1
x_{k+1}
xk+1后接着计算
f
(
x
k
+
1
)
f(x_{k+1})
f(xk+1),如果
∣
f
(
x
k
+
1
)
∣
<
∣
f
(
x
k
)
∣
|f(x_{k+1})|<|f(x_{k})|
∣f(xk+1)∣<∣f(xk)∣成立,则
x
k
+
1
x_{k+1}
xk+1为第k+1步的迭代值。再取
λ
\lambda
λ按照上一步接着计算
x
k
+
2
x_{k+2}
xk+2,如果计算过程中遇到一个迭代值
x
k
x_{k}
xk取不到满足要求的
λ
\lambda
λ值,则称“下山失败”。这时需要另取初始值
x
0
x_{0}
x0进行重新计算。
多根区间上的逐次逼近法
方程f(x)=0在多根区间[a,b]上,根的情况无非两种。均为单根或有重根。我们先看均为单根的情况:
1)首先求出单根区间,假设有m个根。把[a,b]分成n个小区间。
[
b
0
,
b
1
]
,
[
b
1
,
b
2
]
,
.
.
.
[
b
n
−
1
,
b
n
]
,
(
b
0
=
a
,
b
n
=
b
)
[b_0,b_1],[b_1,b_2],...[b_{n-1},b_n],(b_0=a,b_n=b)
[b0,b1],[b1,b2],...[bn−1,bn],(b0=a,bn=b)然后计算
f
(
b
i
)
(
i
=
1
,
2
,
.
.
.
,
n
)
f(b_i)(i=1,2,...,n)
f(bi)(i=1,2,...,n)的值,当
f
(
b
i
)
f
(
b
i
+
1
)
<
0
f(b_i)f(b_{i+1})<0
f(bi)f(bi+1)<0时,那在
[
b
i
,
b
i
+
1
]
[b_i,b_{i+1}]
[bi,bi+1]上至少有一个根。如果有m个区间是这样,那所得到的就都是单根区间。如果这样的有根区间小于m,那就把这些区间再对分,然后重复上述计算直到有m个有根区间为止。
2)再在单根区间上求解。这个就回到之前讲的了。这里介绍一种搜索法。可用来求迭代法的初始值,也可求近似根:


如果发现用二分法过程中,趋于零的速度慢,可以从某个区间开始用迭代法,用该区间端点作为初始值。
再看有重根的情况:

通过计算得出:在重根条件下的Newton 迭代法如果收敛, 必是线性收敛的。为了提高收敛的阶,可取:

这样迭代函数至少是平方收敛。可以看个例子:
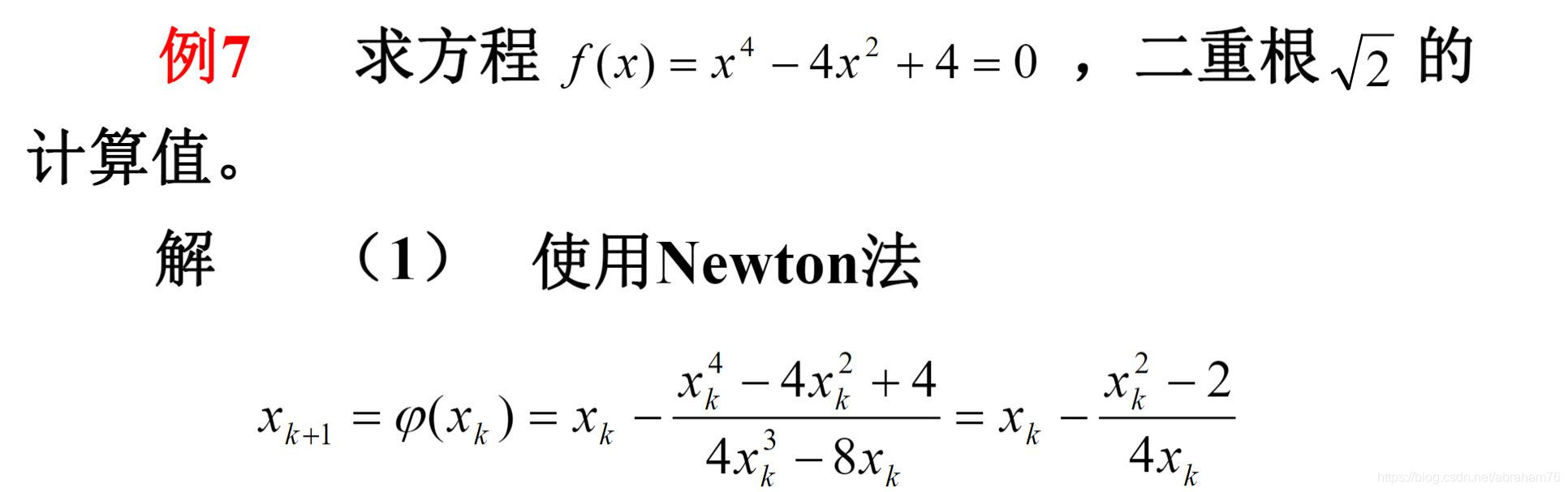









 本文探讨了在科学计算中解决非线性方程的数值方法,特别是简单迭代法。通过迭代函数构造,如x=φ(x),并分析了迭代函数的性质对收敛性的影响。当φ′(x)<1时,迭代法收敛。还介绍了Newton迭代法,以及如何通过选择合适的下山因子确保大范围内的收敛性。在多根区间上,提出了逐次逼近法来寻找根的位置。文章强调了初始值选择、收敛速度阶的概念以及不同情况下的收敛行为。
本文探讨了在科学计算中解决非线性方程的数值方法,特别是简单迭代法。通过迭代函数构造,如x=φ(x),并分析了迭代函数的性质对收敛性的影响。当φ′(x)<1时,迭代法收敛。还介绍了Newton迭代法,以及如何通过选择合适的下山因子确保大范围内的收敛性。在多根区间上,提出了逐次逼近法来寻找根的位置。文章强调了初始值选择、收敛速度阶的概念以及不同情况下的收敛行为。
















 7573
7573

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








