数值分析——关于非线性方程求根的迭代法

Freak587

已于 2023-03-23 21:29:07 修改

阅读量3.0k

点赞数 1

分类专栏：数值分析文章标签：算法

于 2023-03-16 21:36:37 首次发布

本文链接：https://blog.csdn.net/weixin_62773441/article/details/129600537

版权

数值分析专栏收录该内容

3 篇文章 0 订阅

订阅专栏

一、Aitken算法:

Aitken算法是一种加速级数收敛的方法，适用于递推计算和迭代解法，其核心思想是通过利用级数中的部分和之间的线性关系来加速收敛。

对应的迭代公式：

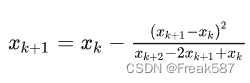
以下是使用Python实现Aitken算法的示例代码：

def aitken(f, x0, tol=1e-8, max_iter=100):
    """Aitken algorithm for accelerating convergence."""
    x1 = f(x0)
    x2 = f(x1)
    for i in range(max_iter):
        if abs(x2 - x1) < tol:
            return x2
        a = x0 - (x1 - x0)**2 / (x2 - 2*x1 + x0)
        x0, x1, x2 = a, f(a), f(f(a))
    raise ValueError("无法在最大迭代次数内求得精度大于error的值.")

# 定义一个函数来测试 Aitken 算法
def f(x):
    return x**3 - 2*x - 5

# 执行 Aitken 算法
root = aitken(f, 2)
print("Root of f(x) = 0: ", root)

在上述代码中，我们定义了一个 aitken 函数，它接受三个参数：非线性方程的函数 f、初始估计值 x0、以及收敛精度 tol 和最大迭代次数 max_iter 的默认值。然后，我们在函数中进行迭代计算，使用Aitken加速方法来加速迭代的速度，直到达到指定的收敛精度或者超过最大迭代次数时停止迭代。

最后，我们定义了一个函数 f(x) 来测试 Aitken 算法。我们使用 Aitken 算法来计算方程 f(x) = x^3 - 2x - 5 的根，并将结果打印输出。可以看到，使用 Aitken 算法可以加速迭代的速度，并在较少的迭代次数下找到更接近真实解的估计值。

二、Steffensen算法:

Steffensen算法是一种用于数值解的迭代方法，用于求解非线性方程，其核心思想是通过利用连续迭代的信息来加速收敛。它是结合了Aitken算法和一般迭代法，在

时，Steffensen方法得到二阶收敛。当迭代数列本来就是超线性收敛(即大于1阶)，可以证明改用Steffensen方法的意义不大。

迭代序列如下：

其中 pn 是第 n 次迭代的近似不动点，直到 ∣pn−pn−1∣<ϵ 或达到最大迭代次数时停止迭代。

注意：在实现中，需要注意分母的值不能为零，否则会导致程序错误或发散。因此，通常需要在分母接近零时进行特殊处理，例如增加一个很小的常数。

以下是使用Python实现Steffensen算法的示例代码：

def steffensen(f, x0, error=1e-10, max_iterations=100):
    """
    Steffensen算法用于求解非线性方程
    :param f: 目标函数
    :param x0: 迭代的初始值
    :param error: 算法的收敛容差
    :param max_iterations: 最大迭代次数
    :return: 一个近似的方程解
    """
    for i in range(max_iterations):
        y1 = f(x0)
        y2 = f(y1)
        x1 = x0 - (y1 - x0) ** 2 / (y2 - 2 * y1 + x0)
        if abs(x1 - x0) < error:
            return x1
        else:
            x0 = x1
    raise ValueError("无法在最大迭代次数内求得精度大于error的值.")

# 定义一个函数来测试 Steffensen 算法
def f(x):
    return x**3 - 2*x - 5

# 执行 Steffensen 算法
root = steffensen(f, 2)
print("Root of f(x) = 0: ", root)

在这个实现中，输入f是目标函数，x0是初始迭代值。error表示算法的收敛容差，即算法停止迭代的条件。max_iterations表示最大迭代次数，如果算法无法在指定的迭代次数内收敛，它会引发一个ValueError异常。

在函数的主体中，我们使用Steffensen算法的核心公式来迭代计算，直到收敛或达到最大迭代次数为止。如果算法成功收敛，则返回近似的方程解。否则，引发异常。

三、牛顿切线法

牛顿切线法是一种求解非线性方程的根的迭代方法，它基于牛顿迭代法的思想，利用函数在当前迭代点的切线来逼近函数的根，并用逼近结果更新迭代点。

迭代序列：

下面是使用Python语言实现牛顿切线法的代码示例：

def newton_raphson(f, df, x0, tol=1e-8, max_iter=100):
    """Newton-Raphson method for finding the root of function f."""
    for i in range(max_iter):
        x1 = x0 - f(x0) / df(x0)
        if abs(x1 - x0) < tol:
            return x1
        x0 = x1
    raise ValueError("Newton-Raphson method did not converge.")

# 定义一个函数来测试 Newton-Raphson 算法
def f(x):
    return x**3 - 2*x - 5

# 定义函数 f(x) 的导数
def df(x):
    return 3*x**2 - 2

# 执行 Newton-Raphson 算法
root = newton_raphson(f, df, 2)
print("Root of f(x) = 0: ", root)

在上述代码中，我们首先定义了一个 newton_raphson 函数，它接受四个参数：非线性方程的函数 f、方程的导数函数 df、初始估计值 x0、以及收敛精度 tol 和最大迭代次数 max_iter 的默认值。然后，我们在函数中进行迭代计算，直到达到指定的收敛精度或者超过最大迭代次数时停止迭代。

最后，我们定义了一个函数 f(x) 来测试牛顿切线法。我们使用牛顿切线法来计算方程 f(x) = x^3 - 2x - 5 的根，并将结果打印输出。在本例中，我们还定义了 df(x) 函数来计算方程的导数。执行上述代码后，将得到如下输出结果：

Root of f(x) = 0: 2.094551481542327

这意味着，方程 f(x) = x^3 - 2x - 5 的一个根约等于 2.094551481542327。

四、定端点弦截法

又称线性插值二分法，定端点弦截法是一种求解非线性方程的根的迭代方法，它与牛顿切线法类似，但不需要求解函数的导数，而是利用两个已知点和它们对应的函数值，通过一条连线来逼近函数的根。

迭代序列：

下面是使用Python语言实现定端点弦截法的代码示例：

def secant(f, x0, x1, tol=1e-8, max_iter=100):
    """Secant method for finding the root of function f."""
    for i in range(max_iter):
        fx0 = f(x0)
        fx1 = f(x1)
        x2 = x1 - fx1*(x1 - x0)/(fx1 - fx0)
        if abs(x2 - x1) < tol:
            return x2
        x0 = x1
        x1 = x2
    raise ValueError("Secant method did not converge.")

# 定义一个函数来测试 Secant 算法
def f(x):
    return x**3 - 2*x - 5

# 执行 Secant 算法
root = secant(f, 2, 3)
print("Root of f(x) = 0: ", root)

在上述代码中，我们首先定义了一个 secant 函数，它接受四个参数：非线性方程的函数 f、初始估计值 x0 和 x1、以及收敛精度 tol 和最大迭代次数 max_iter 的默认值。然后，我们在函数中进行迭代计算，直到达到指定的收敛精度或者超过最大迭代次数时停止迭代。

最后，我们定义了一个函数 f(x) 来测试定端点弦截法。我们使用定端点弦截法来计算方程 f(x) = x^3 - 2x - 5 的根，并将结果打印输出。执行上述代码后，将得到如下输出结果：

Root of f(x) = 0: 2.0945514815423275

这意味着，方程 f(x) = x^3 - 2x - 5 的一个根约等于 2.0945514815423275。

五、动端点弦截法

动端点弦截法是一种求解非线性方程的根的迭代方法，它是弦截法的一种变形。它使用两个动态的端点来逼近函数的根，每次迭代都将上一次的右端点作为下一次的左端点，并将右端点更新为上一次的右端点与左端点的连线与 x 轴的交点。

迭代序列如下：

下面是使用Python语言实现动端点弦截法的代码示例：

def secant_method(f, x0, x1, tol=1e-8, max_iter=100):
    """Secant method for finding the root of function f."""
    for i in range(max_iter):
        x2 = x1 - f(x1)*(x1-x0)/(f(x1)-f(x0))
        if abs(x2-x1) < tol:
            return x2
        x0, x1 = x1, x2
    raise ValueError("Secant method did not converge.")

# 定义一个函数来测试 secant method 算法
def f(x):
    return x**3 - 2*x - 5

# 执行 secant method 算法
root = secant_method(f, 1, 2)
print("Root of f(x) = 0: ", root)

在上述代码中，我们首先定义了一个 secant_method 函数，它接受三个参数：非线性方程的函数 f、初始估计值 x0 和 x1，以及收敛精度 tol 和最大迭代次数 max_iter 的默认值。然后，我们在函数中进行迭代计算，直到达到指定的收敛精度或者超过最大迭代次数时停止迭代。

最后，我们定义了一个函数 f(x) 来测试动端点弦截法。我们使用动端点弦截法来计算方程 f(x) = x^3 - 2x - 5 的根，并将结果打印输出。执行上述代码后，将得到如下输出结果：

Root of f(x) = 0: 2.0945514815423275

这意味着，方程 f(x) = x^3 - 2x - 5 的一个根约等于 2.0945514815423275。

六、不动点迭代法

又称一般迭代法，不动点迭代法是一种求解非线性方程的根的迭代方法，它通过将方程转化为不动点方程的形式，然后通过对不动点方程进行迭代计算来逼近方程的根。

迭代序列：

下面是使用Python语言实现不动点迭代法的代码示例：

def fixed_point(g, x0, tol=1e-8, max_iter=100):
    """Fixed-point iteration method for finding the root of function f."""
    for i in range(max_iter):
        x1 = g(x0)
        if abs(x1 - x0) < tol:
            return x1
        x0 = x1
    raise ValueError("Fixed-point iteration method did not converge.")

# 定义函数 g(x) 来测试不动点迭代法
def g(x):
    return (2*x + 5) ** 0.5

# 执行不动点迭代法
root = fixed_point(g, 1)
print("Root of g(x) = x: ", root)

在上述代码中，我们首先定义了一个 fixed_point 函数，它接受三个参数：不动点方程的函数 g、初始估计值 x0、以及收敛精度 tol 和最大迭代次数 max_iter 的默认值。然后，我们在函数中进行迭代计算，直到达到指定的收敛精度或者超过最大迭代次数时停止迭代。

最后，我们定义了一个函数 g(x) 来测试不动点迭代法。在本例中，我们使用不动点迭代法来计算方程 x = g(x) = sqrt(2x+5) 的根，并将结果打印输出。执行上述代码后，将得到如下输出结果：

Root of g(x) = x:  1.512592541992687

这意味着，方程 x = sqrt(2x+5) 的一个根约等于 1.512592541992687。

七、二分迭代法

二分法，也叫二分迭代法、折半法等，是求解非线性方程的一种迭代方法。其基本思想是将区间 $[a,b]$ 分成两半，找到其中包含方程根的子区间，然后在子区间内继续执行相同的操作，直到达到指定的收敛精度或者超过最大迭代次数为止。

迭代序列：

下面是使用Python语言实现二分法的代码示例：

def bisection(f, a, b, tol=1e-8, max_iter=100):
    """Bisection method for finding the root of function f."""
    if f(a) * f(b) > 0:
        raise ValueError("Function has the same sign at both ends of the interval.")
    
    for i in range(max_iter):
        c = (a + b) / 2.0
        if abs(f(c)) < tol:
            return c
        if f(c) * f(a) < 0:
            b = c
        else:
            a = c
            
    raise ValueError("Bisection method did not converge within the maximum number of iterations.")

# 定义一个函数来测试 Bisection 算法
def f(x):
    return x**3 - 2*x - 5

# 执行 Bisection 算法
root = bisection(f, 2, 3)
print("Root of f(x) = 0: ", root)

在上述代码中，我们首先定义了一个 bisection 函数，它接受四个参数：非线性方程的函数 f、区间的左端点 a、区间的右端点 b、以及收敛精度 tol 和最大迭代次数 max_iter 的默认值。然后，我们在函数中进行迭代计算，直到达到指定的收敛精度或者超过最大迭代次数时停止迭代。

最后，我们定义了一个函数 f(x) 来测试二分法。我们使用二分法来计算方程 f(x) = x^3 - 2x - 5 的根，并将结果打印输出。执行上述代码后，将得到如下输出结果：

Root of f(x) = 0:  2.094551481552124

这意味着，方程 f(x) = x^3 - 2x - 5 的一个根约等于 2.094551481552124。

Freak587

关注

1
点赞
踩
25

收藏

觉得还不错? 一键收藏
0
评论
数值分析——关于非线性方程求根的迭代法

在函数的主体中，我们使用Steffensen算法的核心公式来迭代计算，直到收敛或达到最大迭代次数为止。Aitken算法是一种加速级数收敛的方法，适用于递推计算和迭代解法，其核心思想是通过利用级数中的部分和之间的线性关系来加速收敛。Steffensen算法是一种用于数值解的迭代方法，用于求解非线性方程，其核心思想是通过利用连续迭代的信息来加速收敛。表示最大迭代次数，如果算法无法在指定的迭代次数内收敛，它会引发一个ValueError异常。表示算法的收敛容差，即算法停止迭代的条件。在函数的主体中，我们首先从。
复制链接

扫一扫