POJ 1961 Period（KMP思想的应用）

要解这道题，一定要明白next数组每次如果不匹配一次向前找的原理。

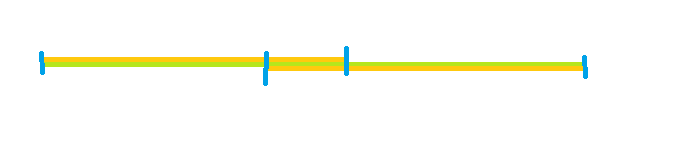
如下图1：这里面，假设这个线段是一个字符串，那么下面我们来说一下，为什么一直取next就可以找到找到next的值。首先我假设我们从第三段最后一个位置发现s[j] != s[k]了，那么我们只清楚的是的前一个是指向粉色线段的末尾的，那么也就是说粉色线段和红色的线段标记的这两段字符串是相等的。当发生s[j]和s[k]不等的时，k要向前寻找，假设这时，next[k]的值恰好指向了第一蓝色线段的末尾，那么也就是说前两个蓝色线段相等， 又因为，粉色和红色相等，所以红色的半部分的蓝色和粉色后半部分的蓝色（长度相同）必然相等，因此，粉色前面的蓝色必然和红色后面的蓝色相等，即三条蓝色线段必然相等。那么如果这时候，也就是第一个箭头的位置，和j位置的字符相等(s[k] == s[j])，那么必然在当前字符串的长度的情况下，最长相等前缀和后缀的长度，就是蓝色部分+1。

这里的重点在于三条蓝色线段相等！

接下来解释用这个原理来解这道题。

这道题的大意是说，判断给定的字符串，所有长度大于2的前缀是不是周期字符串。所谓周期字符串就是某一个子串连续出现k次，比如aaa，当前缀aa的时候，a出现了两次，那么aa就是周期字符串，再比如aabaabaab，取它的前缀长度为6的时候，aabaab，这是也是周期字符串，aab周期出现，并且出现两次。最后，如果某个前缀是前缀字符串的话，在单独一行输出前缀的长度，和k的最大值。其中，k必须满足大于1.

对于这个问题，其实就是GetNext这个函数少做改动，看了下面的图，结合上面的说的就显而易见了：

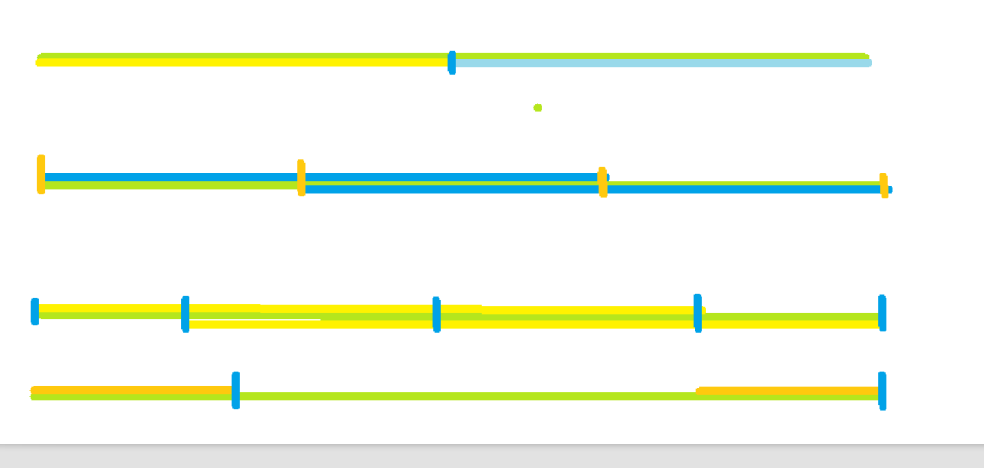
首先要明确一点，想要k值最大，那么循环的字符串必须是最小的，因此，找到最长前缀同时又是最长后缀的字符串，前缀的最后的位置和后缀的最后的位置差值必定最小，那么也必然使得k值最大。因此要找最大既是前缀又是后缀的字符串的前缀的末位位置。

然后我们先看第一线段，和上面一样就是一个字符串。这个表示最长前缀同时又是最大后缀的字符串正好是黄色和浅绿色的线段，它们正好将整个字符串分成两半，很显然，这个字符串是周期字符串，k为2.

第二条，绿色线段是整个字符串，上下的蓝色分别是前缀和后缀，假设这个图中的黄色的点将整个字符串分为长度相等的三部分，同时第一部分和第三部分是前缀和后缀没有重叠的部分，第二部分前后缀和后缀重叠。有前缀和后缀相等可是，第一部分==第二部分，因为长度相等，而且还是前缀和后缀对应的部分，而第二部分上面的部分对应的是第三部分，他们相等，由此可知这三条线段对应的字符串相等，也就是说k为3.

第三条线段，同上。

而第四条线段，我们蓝色点的位置，后一个蓝色点指向前一个蓝色点，说明这个不是一个周四字符串。如何证明，反证法吧。如果它是，那么中间绿色的必然是一个周期串，那么就应该有前一段和后一段相等，类似于第二条和第三条线段一下的，如果它是这样的，那么next指针就不会指向现在的位置，因此，必然不是周期串。或者说，如果是一个周期串，同时是最长前缀也是最长后缀的前缀的最后一个位置的下一位一直到字符串首尾，就是这个周期串的最小循环字符串。而如果它不是话，就像第四条和第五条，它的前缀的后位置的下一位到字符串的最后一位的长度，是不会满足是这个字符串的长度的因数的。由此，可得的条件是，当j为当前字符串的长度，最长前缀的长度是k，那么有且仅有满足这个条件：j%（j-k）== 0 && j/(j-k) >1，字符串才是周期字符串，而且K为 j/(j-k)。

代码如下：

#include <cstdio>
#include <cstring>

const int N = 1000000;
int n, next[N];
char str[N];

void getNext()
{
    int j, k;
    next[0] = -1, k = -1, j = 0;
    while ( j < n ) {
        if ( k == -1 || str[j] == str[k] ) {
            j++, k++;
            //printf("%d %d\n", j,k);
            if ( j%(j-k) == 0 && j/(j-k) > 1 ){
                printf("%d %d\n", j, j/(j-k));
            }
            next[j] = k;
        }
        else 
            k = next[k];
    }
}
int main()
{
    int icase = 1;
    while ( scanf("%d", &n) != EOF && n ) {
        getchar();
        scanf("%s", str);
        //printf("%s", str);
        printf("Test case #%d\n", icase++);
        getNext();
        printf("\n");
    }
}