上一次我们分享了多变量线性回归模型(Linear Regression with Multiple Variables),这一次我们来讨论一下多项式回归(Polynomial Regression)和正规方程(Normal Equation)。(我们还是讨论房价预测的问题)
多项式回归
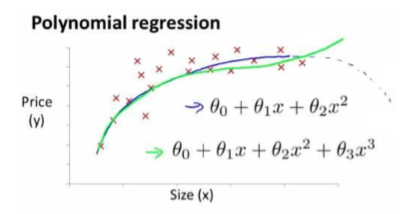
有时候,线性回归并不适用于所有全部的数据,我们需要曲线来适应我们的数据,比如一个二次方模型:
或者一个三次方模型:
这两个模型我们在坐标系绘图如下:
通常情况,我们需要先观察数据然后再去决定使用怎样的模型来处理问题。
除此之外,我们还可以使 :
这样便将高阶方程模型转换成线性回归模型。这也算是特征缩放(Features Scaling)的一种。
PS : 如果我们的模型采用多项式回归模型,在运行梯度下降算法之前,特征缩放是非常有必要的。
正规方程
到目前为止,我们学习讨论的机器学习算法,都是梯度下降算法(Grandient Descent)。但是对于某些回归问题,还有一种更好的解决方案,正规方程。
正规方程是通过求解下面的方程来找出使得代价函数最小的参数:
假设我们的训练特征矩阵为X(包含了X0=1)并且我们的训练集结果为向量 y ,则利用正规方程解出向量 :
标注:T表示矩阵X的转置,-1 表示矩阵X的逆
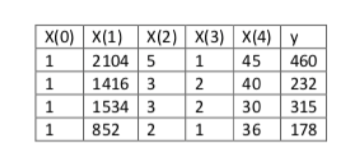
我们使用房价预测问题的数据:
数据包括四个特征(不包括X0),我们加入X0=1,这时候我们使用正规方程方法来求解:
在Matlab中,正规方程写作:pinv(X' * X)*X'*y
这里有一个需要注意的地方,有些不可逆的矩阵(通常是因为特征之间并不独立,比如同时包含英尺为单位的尺寸和米为单位的尺寸这两个特征,也有可能是特征数量大于训练集的数量,比如有2000个特征但是只有1000个训练集),正规方程方法是不能够使用的。
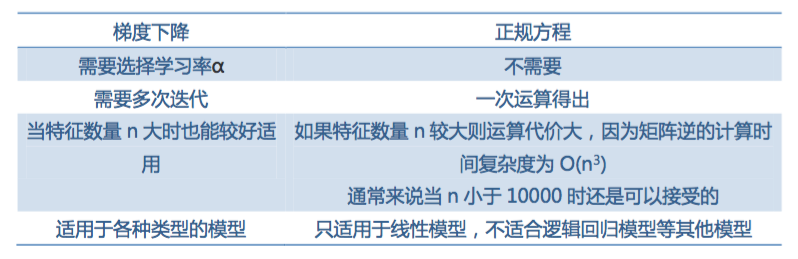
那么我们现在有两个机器学习的算法了,一个是梯度下降,一个是正规方程,两个方法比较如下:
至此,线性回归的问题我们就讨论到这儿。下一阶段我们将讨论逻辑回归问题(Logistic Regression)。











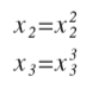
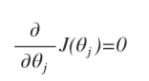
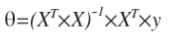
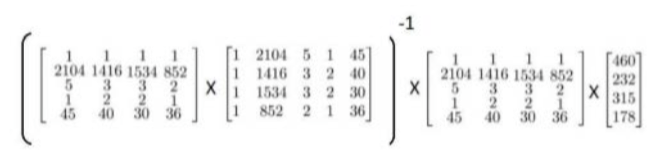














 4722
4722

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








