D - Coloring Dominoes( AtCoder Beginner 071)

Problem Statement
We have a board with a 2×N grid. Snuke covered the board with N dominoes without overlaps. Here, a domino can cover a 1×2 or 2×1 square.

Then, Snuke decided to paint these dominoes using three colors: red, cyan and green. Two dominoes that are adjacent by side should be painted by different colors. Here, it is not always necessary to use all three colors.

Find the number of such ways to paint the dominoes, modulo 1000000007.

The arrangement of the dominoes is given to you as two strings S1 and S2 in the following manner:

Each domino is represented by a different English letter (lowercase or uppercase).
The j-th character in Si represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
Constraints
1≤N≤52
|S1|=|S2|=N
S1 and S2 consist of lowercase and uppercase English letters.
S1 and S2 represent a valid arrangement of dominoes.
Input
Input is given from Standard Input in the following format:

N
S1
S2
Output
Print the number of such ways to paint the dominoes, modulo 1000000007.

Sample Input 1
Copy
3
aab
ccb
Sample Output 1
Copy
6
There are six ways as shown below:

Sample Input 2
Copy
1
Z
Z
Sample Output 2
Copy
3
Note that it is not always necessary to use all the colors.

Sample Input 3
Copy
52
RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn
RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn
Sample Output 3
Copy
958681902

题意就是遇到相同字母用一个1*2或2*1的矩形填充，矩形有三个颜色，相同颜色的不能放在一起，求有多少种放法。
比赛时想到搜索，后来觉得越做越麻烦，后来开始找规律最后也没找到。
参考题解说一下。

将矩形分为两类，竖着放的为X，横着的放为Y。开始X:sum=3，Y:sum=6;

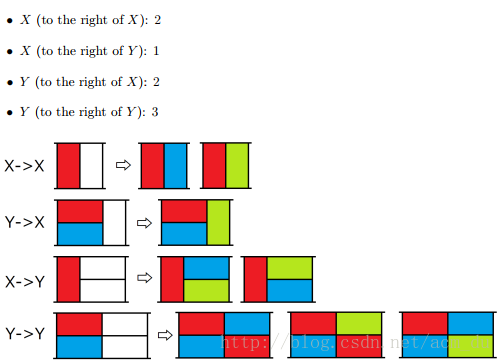
然后从左到右放。
X -> X : sum*2;
X -> Y : sum*2;
Y -> X : sum*1;
Y -> Y : sum*3;

AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#define MOD 1000000007

using namespace std;

int main()
{
    int n;
    char a[55],b[55];
    while(scanf("%d",&n)!=EOF)
    {
        getchar();
        scanf("%s",a);
        getchar();
        scanf("%s",b);
        int i=0,p=0;
        long long sum=1;
        while(i<n)
        {
            if(i==0)
            {
                if(a[i]==b[i])
                {
                    sum=(sum*3)%MOD;
                    i++;
                    p=1;
                }
                else
                {
                    sum=(sum*6)%MOD;
                    i+=2;
                    p=2;
                }
            }
            else
            {
                if(a[i]==b[i])
                {
                    if(p==1)
                    {
                        sum=(sum*2)%MOD;
                    }
                    else
                    {
                        sum=(sum*1)%MOD;
                    }
                    i++;
                    p=1;
                }
                else
                {
                    if(p==1)
                    {
                        sum=(sum*2)%MOD;
                    }
                    else
                    {
                        sum=(sum*3)%MOD;
                    }
                    i+=2;
                    p=2;
                }
            }
        }
        printf("%lld\n",sum);
    }
    return 0;
}