循环冗余校验（CRC校验）

循环冗余校验（CRC校验）

1、基本概念

     循环冗余校验码：是数据通信领域中最常用的一种差错校验码，其特征是信息字段和校验字段的长度可以任意选定。

     循环冗余检查是一种数据传输检错功能，对数据进行多项式计算，并将得到的结果附在帧的后面，接收设备也执行类似的算法以保证数据传输的正确性和完整性。

2、根本思想

     先在要发送的帧后面附加一个数（这个就是用来校验的校验码，但要注意，这里的数也是二进制序列的，下同），生成一个新帧发送给接收端。当然，这个附加的数不是随意的，它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除（注意，这里不是直接采用二进制除法，而是采用一种称之为“模2除法”）。到达接收端后，再把接收到的新帧除以（同样采用“模2除法”）这个选定的除数。因为在发送端发送数据帧之前就已通过附加一个数，做了“去余”处理（也就已经能整除了），所以结果应该是没有余数。如果有余数，则表明该帧在传输过程中出现了差错。

   【说明】“模2除法”
     模2加法运算为：
     1+1=0，0+1=1，0+0=0，无进位，也无借位；
     模2减法运算为：
     1-1=0，0-1=1，1-0=1，0-0=0，也无进位，无借位。
     相当于二进制中的逻辑异或运算。也就是比较后，两者对应位相同则结果为“0”，不同则结果为“1”。
3、CRC校验原理
    具体来说，CRC校验原理就是以下几个步骤：
   （1）先选择一个用于在接收端进行校验时，对接收的帧进行除法运算的除数（是二进制比较特串，通常是以多
项方式表示，所以CRC又称多项式编码方法，这个多项式也称之为“生成多项式”）。
   （2）看所选定的除数二进制位数（假设为k位），然后在要发送的数据帧（假设为m位）后面加上k-1位“0”，
然后以这个加了k-1个“0“的新帧（一共是m+k-1位）以“模2除法”方式除以上面这个除数，所得到的余数（也是二
进制的比特串）就是该帧的CRC校验码，也称之为FCS（帧校验序列）。但要注意的是，余数的位数一定要是比除数位
数只能少一位，哪怕前面位是0，甚至是全为0，也都不能省略。
   （3）再把这个校验码附加在原数据帧（就是m位的帧，注意不是在后面形成的m+k-1位的帧）后面，构建一个新
帧发送到接收端；最后在接收端再把这个新帧以“模2除法”方式除以前面选择的除数，如果没有余数，则表明该帧在
传输过程中没出错，否则出现了差错。
4、生成步骤

 
 

  
   1、将X的最高次幂为R的生成多项式G(X)转换成对应的R+1位二进制数。
 
 
 
 

  
   2、将信息码左移R位，相当于对应的信息多项式C(X)*2R。
 
 
 
 

  
   3、用生成多项式（二进制数）对信息码做除，得到R位的余数(注意：这里的二进制做除法得到的余数其实是模2除
  
  法得到的余数，并
  
  不等于其对应十进制数做除法得到的余数)。
 
 
 
 

  
   4、将余数拼到信息码左移后空出的位置，得到完整的CRC码。
 
 
5、CRC校验码的计算

      CRC校验的关键是如何求出余数，也就是校验码（CRC校验码）。
    下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为，要求出二进制序
列10110011的CRC校验码。下面是具体的计算过程：
   （1）首先把生成多项式转换成二进制数，由可以知道（它一共是6位，总位数等于最高位的
幂次加1，即5+1=6），然后根据多项式各项的含义（多项式只列出二进制值为1的位，也就是这个二进制的第5位、第
4位、第2位、第0位的二进制均为1，其它位均为0）很快就可得到它的二进制比特串为110101。
   （2）因为生成多项式的位数为6，根据前面的介绍，得知CRC校验码的位数为5（校验码的位数比生成多项式的位
数少1）。因为原数据帧10110011，在它后面再加5个0，得到1011001100000，然后把这个数以“模2除法”方式除以生
成多项式，得到的余数（即CRC码）。注意参考前面介绍的“模2除法”运算法则。
                                     
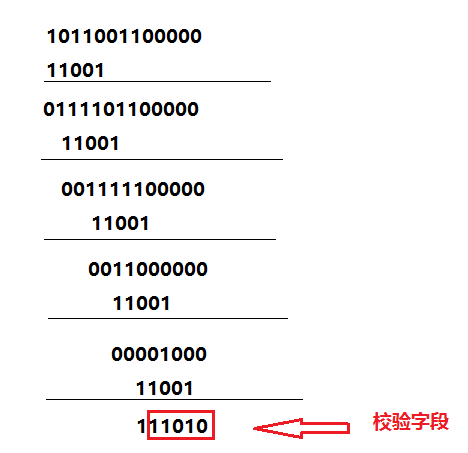
    （3）把上步计算得到的CRC校验11010替换原始帧1011001100000后面的五个“0”，得到新帧1011001111010。
再把这个新帧发送到接收端。
                                                
    （4）当以上新帧到达接收端后，接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除，验证
余数是否为0，如果为0，则证明该帧数据在传输过程中没有出现差错，否则出现了差错。
      CRC进行检错的过程可简单描述为：在发送端根据要传送的k位二进制码序列，以一定的规则产生一个校验用的r
位监督码（CRC码），附在原始信息的后边，构成一个新的二进制码序列数共为k+r位，然后发送出去。在接收端，根
据信息码和CRC码之间所遵循的规则进行检验，以确定传送中是否出错。这个规则，在差错控制理论中称为“生成多项式”。