目录
第1章 质点运动学
第一节 参考系坐标系
运动的决定性与相对性:运动是普遍的、绝对的,但运动的描述是相对的
参考系:为了描述一个物体的运动,被选取、且能用来描述物体运动状态的另一个物体
坐标系:为了定量描述物体的运动,在选定的参考系上建立的带有数学标尺的坐标
运动学中常用的坐标系:直角坐标系 极坐标系 自然坐标系
直角坐标系
矢量表示: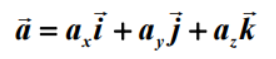
矢量大小: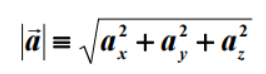
矢量方向:可以用矢量与三个坐标轴(ox、oy、oz)之间的夹角表示
单位矢量:

坐标轴的单位矢量是常矢量,即
矢量对时间求导:
极坐标系:原点o的固定直线、射线(极轴)
极坐标系单位矢量:r。t
矢量表示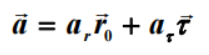
矢量的模
极坐标系极轴方向一般要改变,所以
极坐标系矢量求导:
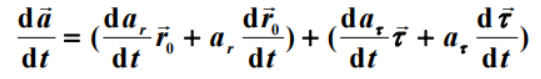

自然坐标系
在已知运动轨道上任取一点为坐标原点 o,以质点所在位置处轨道的切线方向和法线方向作为坐标轴方向
自然坐标系矢量表示
自然坐标系矢量的模
自然坐标系t矢量和曲率,曲率半径有关
曲率:K=dθ/ds
曲率半径:R=1/K
曲率圆
质点模型:理想模型
第二节 位置矢量 位移
位置矢量:质点空间位置的物理参量
位置矢量位置
位置矢量大小(模)r
位置矢量方向
单位矢量
运动方程:矢量随时间变化的函数式
r向量(t)=Ai向量+Bj向量(A,B中必有t)
直角坐标系运动方程:ijk或者x(t)=g(t)yz轨道参数方程
轨道方程:f(X,y,z)=0
位移:位置矢量之差△r向量
位移大小
路程
位移与路程:|dr|=ds
|△r向量|=向量之差
△r=向量模之差
第三节 速度 加速度
平均速度: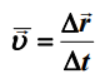
平均速度的大小:
平均速度无法判断质点静止还是运动
瞬时速度:
瞬时速率: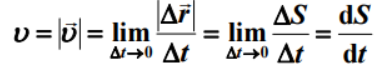
极坐标系t时刻的位置矢量:
极坐标系速度矢量:
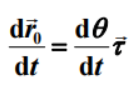
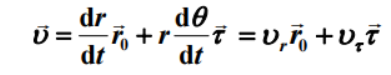
径向速度:大小变化率
切向速度:方向变化率
平均加速度:a向量加杠=△v向量/△t
加速度:a向量=dv向量/dt=dr向量平方/dt的平方
加速度方向
直角坐标系加速度表示
直角坐标系加速度大小
自然坐标系速度v向量=v×切线向量
自然坐标系加速度
自然坐标系切向加速度
自然坐标系法向加速度
自然坐标系加速度大小
an=0直线,≠0曲线
a切=0匀速率,≠0变速率
第四节 角参量
角参量使用场景:圆周运动、刚体定轴转动
角参量:角位移
角位移:在t 时间内,质点位矢转过的角度
![]() 标量:逆时针转动角位移为正,顺时针转动为负
标量:逆时针转动角位移为正,顺时针转动为负
角速度: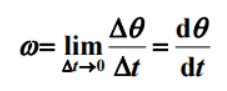
角速度矢量的方向:垂直于质点的运动平面,其指向由右手螺旋定则确定,如图所示
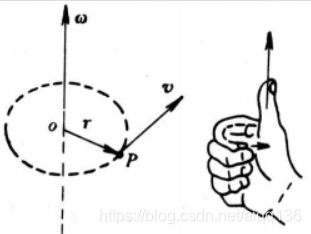
角加速度:
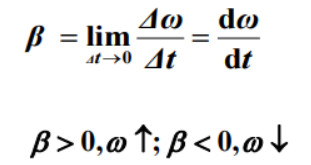
角参量与线参量之间的关系:
t 时间内,质点走过的路程
![]()

圆周运动与直线运动的比较

例题



第五节 运动学的两类问题
描述一般曲线运动的两类问题
已知质点运动方程,求任一时刻的速度、加速度。
• 求解此类问题的基本方法是微分法

已知质点的加速度及初始状态,求质点的运动方程。
解决此类问题的基本方法是积分法






第六节 相对运动
相对运动:研究的是在不同的参考系中,对同一物体运动的数学描述之间的变换关系。
伽利略变换:设参考系 S 和 S′之间只有平动没有转动,各对应坐标轴在运动中始终保持平行。在两个参考系中描述质点P的运动



这三个变换式称为伽利略变换公式,均是矢量关系式,可以表述为:绝对参量=相对参量+牵连参量
注意:伽利略变换是经典力学中的变换式。
它们建立在牛顿的绝对时空观 (长度、时间的测量不依赖于参考系) 基础上,只有在运动速度远小于光速时才成立。
若参考系 S 和 在 t =
= 0 时刻坐标原点 o 和
重合,且
相对 S 沿x轴以速度u 匀速运动。则伽利略变换可写为


伽利略变换的应用
(1) 应用方法
确定描述对象,选择静止系(S系)和运动参照系(系)
确定绝对参量,相对参量,牵连参量
利用伽利略变换式
列方程并求解
(2) 应用举例



第2章 质点动力学
第一节 质点动力学中的作用力
力的定义:力是物体间的相互作用。从力与质点运动关系看,力是质点运动状态发生改变的原因
四种基本作用力:
| 力的种类 | 作用对象 | 力的强度 | 力程 |
| 万有引力 | 一切质点 | 无穷远 | |
| 电磁作用力 | 带电粒子 | 无穷远 | |
| 强相互作用 | 强子 | 1 | |
| 弱相互作用 | 放射衰变过程 | 小于 |
质点力学中常见的力:
(1) 万有引力:一切物体都具有相互吸引的作用力

引力常量:![]()
引力质量 :m1、m2 表征了两个物体产生与感受引力的量度
(2) 弹性力:两个接触且发生了形变的物体之间的作用力称之为弹性力。
方向:与形变方向相反
弹簧弹性力(胡克定律):F=-kx
(3) 摩擦力
A) 滑动摩擦
接触且有相对滑动的两个物体之间,与物体的相对运动方向相反。
![]()
μk为滑动摩擦系数,N为正压力
B) 静摩擦
两个接触且有相对运动趋势的物体之间,与物体的相对运动趋势方向相反。
![]()
μs为静摩擦系数,N为正压力
物体受到的静摩擦力是一个变力,要在具体问题中具体分析。
摩擦系数的大小取决于物体的材料、表面光滑程度等,通常由实验确定。
(4) 静电作用力(库仑力)
静止电荷间的作用力称之为静电力。

静电力方向:质点连线,作用于受力点电荷;同种电荷互斥,异种电荷相吸
(5) 磁场作用力
磁场对运动电荷的作用称之为洛伦兹力
F=qvB
磁力的方向:满足右手螺旋定则
第二节 力对物体的瞬时动力学效应——牛顿三定律
牛顿运动定律
(1) 牛顿第一定律
物体将保持其相对静止或匀速运动状态,直到外力迫使它改变这种状态
• 惯性:物体保持其相对静止或匀速运动状态的内禀属性
• 惯性状态:物体保持相对静止或匀速直线运动的状态
• 惯性系:满足牛顿第一定律的参考系
非惯性系:不满足牛顿第一定律的参考系
• 惯性是保持物体运动状态原因,力是改变物体运动状态原因
(2) 牛顿第二定律
或F=ma
牛顿第二定律定量给出了力、惯性质量、加速度间的关系
瞬时性、矢量性、独立性

惯性质量与力的度量方法
给定标准力与单位质量

给定标准质量与单位力

(3) 牛顿第三定律
作用力和反作用力分别作用于不同物体上,各自产生效应
作用力和反作用力性质相同,大小相等,方向相反,在同一直线上
作用力与反作用力同时存在,同时消失
(4) 牛顿三定律间的关系
- 牛顿第一定律提出惯性、惯性系概念
- 牛顿第二定律给出惯性量度及F、m、a之间的定量关系
- 牛顿第三定律指出受力分析的原则
- 三大定律共同构成牛顿力学体系的基础
牛顿运动定律的应用
(1) 牛顿定律应用的主要类型
已知受力求物体运动状态
已知物体运动状态求物体受力
已知物体部分运动状态和部分力求解未知力和运动状态
(2) 牛顿定律应用的解题步骤
确定研究对象,分析物体受力
建立坐标系,列动力学方程
解算及讨论


第三节 非惯性系与惯性力
1. 非惯性系中的运动
相对于任意惯性系静止或做匀速直线运动的参考系也是惯性系。
非惯性系:相对于已知惯性系做加速运动。
惯性系的选取:地面参考系、地心参考系、太阳参考系。
案例 :s 系相对地面静止; 系以 a 相对 s 系运动。
如何描述在水平方向小球的运动?
s系观察者:小球相对地面加速运动——满足牛顿第二定律
系观察者:小球在水平方向受弹力而静止——牛顿定律失效

2. 平动非惯性系中的牛顿定律



3. 转动非惯性系与离心力
案例:开槽转动圆盘中的小球运动状态分析
地面上观察者:运动状态满足牛顿第二定律
圆盘上观察者:运动状态不满足牛顿第二定律
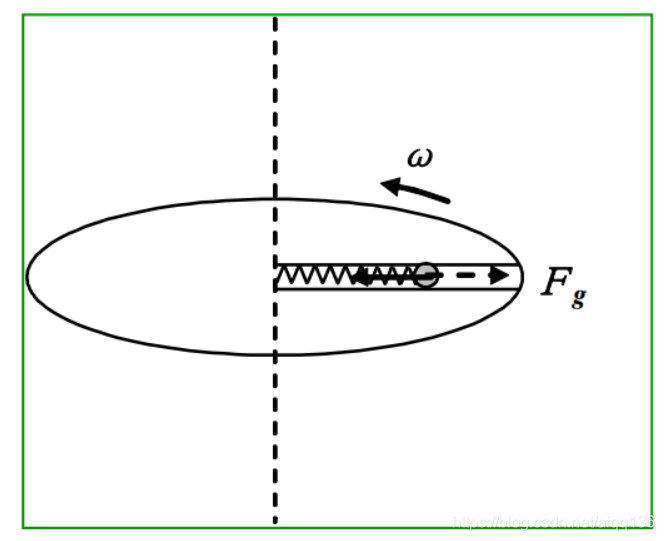
惯性离心力 :由于转动参考系的加速度效应而产生的一个假想力

注意:区别离心力和小球所受的向心力
转动系中静止物体:

运动物体又如何?


4. 转动系中的科里奥利力

第四节 力对物体的时间累积效应——动量定理
第五节 质心与质心运动定理
第六节 力对物体的空间累积效应——功和动能
第七节 功能原理与机械能守恒定律
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








