Phase correlation
In image processing, phase correlation is a method of image registration, and uses a fast frequency-domain approach to estimate the relative translative offset between two similar images.
Contents[hide] |
[edit]Example
The following image demonstrates the usage of phase correlation to determine relative translative movement between two images corrupted by independent Gaussian noise. The image was translated by (30,33) pixels. Accordingly, one can clearly see a peak in the phase-correlation representation at approximately (30,33).
[edit]Method
Given two input images  and
and 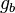 :
:
Apply a window function (e.g., a Hamming window) on both images to reduce edge effects. Then, calculate the discrete 2D Fourier transform of both images.
Calculate the cross-power spectrum by taking the complex conjugate of the second result, multiplying the Fourier transforms together elementwise, and normalizing this product elementwise.
Obtain the normalized cross-correlation by applying the inverse Fourier transform.
Determine the location of the peak in  (possibly using sub-pixel edge detection[clarification needed]).
(possibly using sub-pixel edge detection[clarification needed]).
[edit]Rationale
The method is based on the Fourier shift theorem. Let the two images  and
and 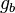 be circularly-shifted versions of each other:
be circularly-shifted versions of each other:
(where the images are 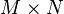 in size).
in size).
Then, the discrete Fourier transforms of the images will be shifted relatively in phase:
One can then calculate the normalized cross-power spectrum to factor out the phase difference:
since the magnitude of an imaginary exponential always is one, and the phase of  always is zero.
always is zero.
The inverse Fourier transform of a complex exponential is a Kronecker delta, i.e. a single peak:
This result could have been obtained by calculating the cross correlation directly. The advantage of this method is that the discrete Fourier transform and its inverse can be performed using thefast Fourier transform, which is much faster than correlation for large images.
[edit]Benefits
Unlike many spatial-domain algorithms, the phase correlation method is resilient to noise, occlusions, and other defects typical of medical or satellite images.[citation needed]
The method can be extended to determine rotation and scaling differences between two images by first converting the images to log-polar coordinates. Due to properties of the Fourier transform, the rotation and scaling parameters can be determined in a manner invariant to translation.[1][2]
[edit]Limitations
In practice, it is more likely that 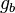 will be a simple linear shift of
will be a simple linear shift of  , rather than a circular shift as required by the explanation above. In such cases,
, rather than a circular shift as required by the explanation above. In such cases,  will not be a simple delta function, which will reduce the performance of the method. In such cases, a window function should be employed during the Fourier transform to reduce edge effects, or the images should be zero padded so that the edge effects can be ignored. If the images consist of a flat background, with all detail situated away from the edges, then a linear shift will be equivalent to a circular shift, and the above derivation will hold exactly.
will not be a simple delta function, which will reduce the performance of the method. In such cases, a window function should be employed during the Fourier transform to reduce edge effects, or the images should be zero padded so that the edge effects can be ignored. If the images consist of a flat background, with all detail situated away from the edges, then a linear shift will be equivalent to a circular shift, and the above derivation will hold exactly.
For periodic images (such as a chessboard), phase correlation may yield ambiguous results with several peaks in the resulting output.
[edit]Applications
Phase correlation is the preferred method for television standards conversion, as it leaves the fewest artifacts.
[edit]See also
General
Television
[edit]References
- ^ E. De Castro and C. Morandi "Registration of Translated and Rotated Images Using Finite Fourier Transforms", IEEE Transactions on pattern analysis and machine intelligence, Sept. 1987
- ^ B. S Reddy and B. N. Chatterji, “An FFT-based technique for translation, rotation, and scale-invariant image registration”, IEEE Transactions on Image Processing 5, no. 8 (1996): 1266–1271.











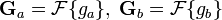


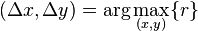
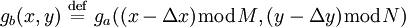
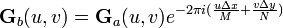
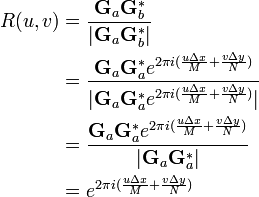















 781
781











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








