本文转载自:https://blog.csdn.net/sinat_30973431/article/details/85119871
一、01背包
问题描述:给定n个物体(它们的重量为:w1,w2,......,wn,价值为:v1,v2,......,vn) 和 一个承受重量为W的背包,问怎么选取这些物体,放在背包中(不超过背包的承重),让所取的子集达到最大价值。
1、基本实现
首先,我们很自然想到穷举法,只要给出n个物体的所有组合(子集),分别各个子集的总价值,去掉那些总重量超过背包承重W的子集之后,对剩下的子集中找到总价值最大的那一个,就是我们想要的结果了。
但是,由于n各物体的有2^n个子集,所以上面的做法的时间复杂度将是O(2^n),除非n很小,否则时间性能消耗非常严重。
我们换一种思路,如果物体有n-1个,在背包容量为0,1,2,......,W各个情况下所能得到的最大价值都已经知道,那么当我们多考虑一个物体,即物体有n个时,就可以分为两个情况进行考虑:(1)第n个物体不放进背包中;(2)第n个物体放进背包。
对于第一种情况,考虑n个物体,跟考虑n-1个物体没有区别,所以考虑n个物体的情况下,在一定承重量的背包中所能得到的最大价值等于只考虑n-1个物体在同等承重量的背包下所能得到的最大价值。
对于第二种情况,则最大价值 = 物体n的价值vn + 背包在剩余空间(W-wn)下只考虑n-1个物体所能达到的最大价值。
如下面递推式所示,
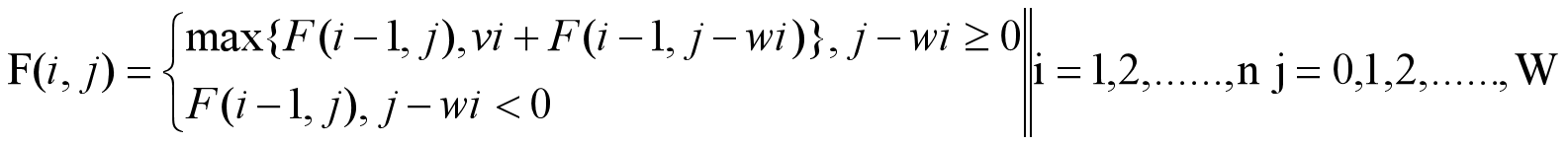
其中,F(i,j)表示前 i 个物体(1≤ i ≤n)在背包承重为 j 时,所能达到的最大价值。如果把它看成一个状态的话,那么也就是说,状态F(i,j)的值等于状态F(i-1,j)、状态F(i-1,j-wi)与vi之和 两者中的最大值。那么要求 i 个物体在一定承重背包中可取的最大价值,只需考虑 i-1 个物体在不同承重量(0,1, 2, ......,W)的背包下可取的最大价值。类似地,要想知道 i-1 个物体在一定承重的背包中可取的最大价值,只需知道 i-2 个物体在不同承重量的背包中可取的最大价值。以此类推,直到所考虑的物体个数变为 1 。
所以,只要我们知道物体个数为 1 时,在不同承重量的背包中所能取到的最大价值,就可以依次求物体个数为2,3,......,n的情况下在不同承重量的背包中所能取的最大价值。
初始条件为:i = 1 当 j ≥ w1时,F(1,j) = v1; 当 0≤ j <w1时,F(1,j) = 0.
知道了上面的递推式、初始条件,就可以写出01背包的代码了。
-
// 二维实现
-
-
public
class PkgTest {
-
public static void main(String[] args) {
-
//w[]:物品重量,v[]:物品价值,m:背包承重,n:物品个数,maxValue[][]:状态
-
int[] w = {
0,
10,
3,
4,
5};
//第一个数为0,是为了让输出时,i表示有i个物品
-
int[] v = {
0,
3,
4,
6,
7};
-
int m =
10;
-
int n =
4;
-
int[][] maxValue =
new
int[
5][
16];
-
-
// 01背包算法
-
for (
int i=
1; i<=n; i++) {
//第一个物体 是 第1行
-
for (
int j=
0; j<=m; j++) {
-
if (i >
0) {
-
maxValue[i][j] = maxValue[i-
1][j];
-
if (j >= w[i]) {
-
maxValue[i][j] = max(maxValue[i][j], maxValue[i-
1][j-w[i]] + v[i]);
-
//注:maxValue[i][j]其实就是maxValue[i-1][j] 因为上面的赋值
-
}
-
}
else {
//初始化,只考虑一个物体
-
if (j >= w[
1]) {
-
maxValue[
1][j] = v[
1];
-
}
-
}
-
}
-
}
-
-
System.out.println(
"4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[n][m]);
-
System.out.println();
-
-
// 打印背包的不同承重量
-
System.out.print(
" " +
"\t");
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(i +
"\t");
-
}
-
System.out.println();
-
-
// 打印01背包算法 得到的状态矩阵值
-
for (
int i=
1; i<=n; i++) {
-
System.out.print(
"i="+ i +
"\t");
-
for (
int j=
0; j<=m; j++) {
-
System.out.print(maxValue[i][j]+
"\t");
-
}
-
System.out.println();
-
}
-
}
-
-
public static int max(int a, int b) {
-
if (a > b) {
-
return a;
-
}
-
return b;
-
}
-
}
结果如下图所示,

2、滚动数组实现
上面的基本实现时间复杂度为O(nW),空间复杂度为O(nW),事实上空间可以做优化。我们可以看到,第 i 层的状态至于第 i-1 层的状态有关,与第 i-2 层的状态没有直接关系,如下面的图所示,除了第一层的初始条件,其他每一层的状态值的求解依赖于上一层。

所以,我们可以用只有两行的二维数组 maxValue[2][ ] 来存储,如下面代码所示。
-
// 滚动数组实现
-
-
public
class PkgTest {
-
public static void main(String[] args) {
-
int[] w = {
0,
10,
3,
4,
5};
-
int[] v = {
0,
3,
4,
6,
7};
-
int m =
10;
-
int n =
4;
-
int k =
0;
// k的作用是指向数组的某一行(两行其中之一),不能再用下标i来指定数组的行数了
-
int[][] maxValue =
new
int[
2][
16];
-
-
for (
int i=
1; i<=n; i++) {
-
for (
int j=
0; j<=m; j++) {
-
if (i >
1) {
-
k = i &
1;
// k = i % 2 获得滚动数组当前索引 k
-
maxValue[k][j] = maxValue[k^
1][j];
// k ^ 1 获得滚动数组逻辑上的“上一行”
-
if (j >= w[i]) {
-
maxValue[k][j] = max(maxValue[k][j], maxValue[k^
1][j-w[i]] + v[i]);
-
}
-
}
else {
-
if (j >= w[
1]) {
-
maxValue[
1][j] = v[
0];
-
}
-
}
-
}
-
}
-
-
System.out.println(
"4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[k][m]);
-
System.out.println();
-
-
System.out.print(
"i=0"+
"\t");
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(maxValue[
1][i] +
"\t");
-
}
-
System.out.print(
"\ni=1"+
"\t");
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(maxValue[
0][i] +
"\t");
-
}
-
}
-
-
public static int max(int a, int b) {
-
if (a > b) {
-
return a;
-
}
-
return b;
-
}
-
}
需要注意的是,代码中我们不再用下标 i 指向数组的索引,而是用 k 指向数组,k=0、k=1表示相邻的两行状态值,k=1不一定是k=0逻辑上的上一行,需要看具体情况(这个把整个过程画一下就知道了)。
初始化时,我们在标号为1的一行输入状态值。
![]()
当 i = 2 大于1时,
由于![]()
![]()
此时 k = 0指向数组的另一行,我们通过 k ^ 1找到 k 逻辑上的“上一行”,并通过“上一行”算出本行中的状态值

以此类推,不断算出并刷新各行的状态值,直到最后两行。
运行结果如下所示,

3、一维数组实现
01背包还可以用一维数组实现,只不过此时的递推式 & 初始条件就需要做些改变了。要想用一维数组存放所有状态,也就是让该数组某个时间是第 i-1 层的状态,而过一段时间之后则成为第 i 层的状态。如下面所演示的,初始状态下,一维数组 maxValue[ ]存放的是 i = 1 时的状态值(对应上面的F[ 1 ][ j ],j = 0,1,2,......,W)
![]()
而当 i = 2 时,我们就需要计算 第二行的状态值,并把它们覆盖到maxValue[ ]一维数组之上。
问题是怎么覆盖呢?如果我们还是跟二维数组一样从前往后遍历数组,覆盖的过程中某一时刻如下图所示,其中数组前面部分是属于 i=2 层的状态值,后面部分属于 i=1 层的状态值。

但是,当我们继续计算并写入 i=2 的状态值时,很有可能用到 i=1 的某个状态值,而这个状态值却已经被覆盖掉了,比如,我们计算 i=2 的maxValue[ 6 ]时,要找到 i=1 的 maxValue[ 3 ] 状态值,本来它应该为0,但却变成4,如果我们用4去计算
maxValue[ 6 ],就会得到错误的结果。
事实上,我们覆盖的过程中,应该采用从后到前的顺序遍历。首先,改写maxValue[ W ]的值。

改写之后,原来maxValue[ W ]的值就由3变为4。接着,改写maxValue[ W-1 ],由于计算 i=2 的maxValue[ W-1 ] 不需要用到 i=1 的maxValue[ W ]状态,所以,maxValue[ W ]的改动不影响maxValue[ W-1 ]的计算。
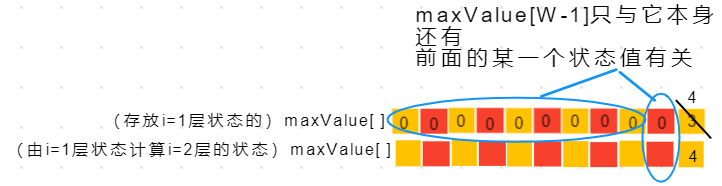
以此类推,就可以在原来的数组上面不断覆盖最新一层的状态值了。
上面的过程的递推式为:
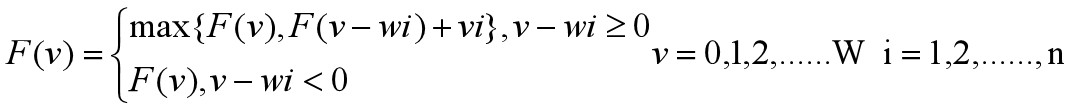
初始条件为:i = 1 当 v≥ w1时,F(v) = v1; 当 0≤ j<w1时,F(v) = 0.
代码实现如下,
-
// 一维数组
-
-
public
class PkgTest {
-
public static void main(String[] args) {
-
int[] w = {
0,
10,
3,
4,
5};
-
int[] v = {
0,
3,
4,
6,
7};
-
int m =
10;
-
int n =
4;
-
//int k = 0;
-
int[] maxValue =
new
int[
16];
-
-
for (
int i=
1; i<=n; i++) {
-
for (
int j=m; j>=w[i]; j--) {
-
maxValue[j] = max(maxValue[j], maxValue[j-w[i]] + v[i]);
-
}
-
-
//验证 结果和二维实现的输出结果完全一样
-
//for (int k=0; k<=m; k++) {
-
// System.out.print(maxValue[k] + "\t");
-
//}
-
//System.out.println();
-
}
-
-
System.out.println(
"4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[m]);
-
System.out.println();
-
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(maxValue[i] +
"\t");
-
}
-
}
-
-
public static int max(int a, int b) {
-
if (a > b) {
-
return a;
-
}
-
return b;
-
}
-
}
运行结果如下所示,

4、小结
尽管滚动数组、一维数组能省一些空间,但是,这两种做法比较适合只求最大价值的需求。当需要输出最佳方案时,我们常常要回溯历史信息,这时,一般就只能用二维数组这种保存有各个状态值的方法了。
这里再稍微讲下滚动数组。事实上,我们可以在一些其它算法看到滚动数组的思想。比如,在斐波那契数列中,我们一般把各个斐波那契数存在一个数组中。但如果我们只需要打印一遍斐波那契数列,或者只需要计算某个斐波那契数时,我们可以只用三个变量(或者三个空间大小的数组),用前两个变量存放初始斐波那契数,然后两者相加之和放在第三个变量。不断地滚动下去,直到求得所需要的斐波那契数。
再比如,二叉树删除一个结点。我们通常让两个引用(或指针)一个指向某个结点,一个指向该节点的父节点。两个引用不断往树深处滚动,直到指向子节点的引用找到待删除节点。这时,我们就可以利用指向父节点的引用对其进行删除了。
二、完全背包
问题描述:完全背包是在01背包的基础上加了个条件——这n种物品都有无限的数量可以取,问怎样拿才可以实现价值最大化。
1、基本实现
虽然题意中每种有无限件,但这里有个隐藏条件:背包承重量的固定性导致每种最多只能取某个值,再多就放不下了,这个值就是W / wi。也就是说,对于第 i 种物品,它可以取0,1,2,......,W / wi(向下取整)件。而在01背包中,对于第 i 种物品,只能取0,1件。我们可以看到,01背包其实就是完全背包的一个特例。所以我们可以用类似01背包的思路写出完全背包的基本算法。
![]()
前面给出的01背包的状态转移方程也可以写成这种形式:
![]()
下面是基本实现的代码,
-
// 完全背包的基本实现
-
-
public
class CompleteTest {
-
public static void main(String[] args) {
-
int[] w = {
0,
10,
3,
4,
5};
-
int[] v = {
0,
3,
4,
6,
7};
-
int m =
10;
-
int n =
4;
-
int[][] maxValue =
new
int[
5][
16];
-
-
for (
int i=
1; i<=n; i++) {
-
for (
int j=
0; j<=m; j++) {
-
if (i >
1) {
-
maxValue[i][j] = maxValue[i-
1][j];
-
//if (j >= v[i]) {
-
// maxValue[i][j] = max(maxValue[i][j], maxValue[i-1][j-v[i]] + w[i]);
-
//}
-
if (j/w[i] >=
1) {
-
int maxTmp =
0;
-
// 对于i个物品,进行j/w[i]次比较得到最大值;而01背包中只需要进行1次比较
-
for (
int k=
1; k<=j/w[i]; k++) {
-
if (maxValue[i-
1][j-k*w[i]] + k*v[i] > maxTmp) {
-
maxTmp = maxValue[i-
1][j-k*w[i]] + k*v[i];
-
}
-
}
-
maxValue[i][j] = max(maxValue[i][j], maxTmp);
-
}
-
}
else {
-
//if (j >= v[0]) {
-
// maxValue[0][j] = w[0];
-
//}
-
if (j/w[
1] >=
1) {
-
maxValue[
1][j] = j/w[
1] * v[
1];
-
}
-
}
-
}
-
}
-
-
System.out.println(
"4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[n][m]);
-
System.out.println();
-
-
// 打印背包的不同承重量
-
System.out.print(
" " +
"\t");
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(i +
"\t");
-
}
-
System.out.println();
-
-
// 打印01背包算法 得到的状态矩阵值
-
for (
int i=
1; i<=n; i++) {
-
System.out.print(
"i="+ i +
"\t");
-
for (
int j=
0; j<=m; j++) {
-
System.out.print(maxValue[i][j]+
"\t");
-
}
-
System.out.println();
-
}
-
}
-
-
public static int max(int a, int b) {
-
if (a > b) {
-
return a;
-
}
-
return b;
-
}
-
}
代码跟01背包的二维数组实现几乎一模一样,我们只需在01背包基本实现的代码中注释掉两段代码,再略微修改就变成完全背包的了。
运行结果如图所示,结果和01背包不同。

2、时间优化
基本实现中的时间复杂度为O(nW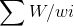
3、空间优化
基本实现采用的是二维数组,事实上我们也可以用一维数组实现。完全背包的一维数组实现和01背包也是几乎完全相同,唯一差别是完全背包的内循环是正向遍历,而01背包的内循环是逆向遍历。
-
// 完全背包的一维数组实现
-
-
public
class CompleteTest2 {
-
public static void main(String[] args) {
-
int[] w = {
0,
10,
3,
4,
5};
-
int[] v = {
0,
3,
4,
6,
7};
-
int m =
10;
-
int n =
4;
-
int[] maxValue =
new
int[
16];
-
-
for (
int i=
1; i<=n; i++) {
-
//for (int j=m; j>=w[i]; j--) {
-
// 正序遍历; 01背包是逆序遍历
-
for (
int j=w[i]; j<=m; j++) {
-
maxValue[j] = max(maxValue[j], maxValue[j-w[i]] + v[i]);
-
}
-
-
//验证 结果和二维实现的输出结果完全一样
-
//for (int k=0; k<=m; k++) {
-
// System.out.print(maxValue[k] + "\t");
-
//}
-
//System.out.println();
-
}
-
-
System.out.println(
"4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[m]);
-
System.out.println();
-
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(maxValue[i] +
"\t");
-
}
-
}
-
-
public static int max(int a, int b) {
-
if (a > b) {
-
return a;
-
}
-
return b;
-
}
-
}
运行结果如下,

三、多重背包
问题描述:多重背包是在01背包的基础上,加了个条件:第 i 件物品有ni件。
1、基本实现
我们考虑一下,如果所有ni都满足ni ≥ W / wi,那不就变成完全背包的问题了么。可见,完全背包的基本实现思路也可以应用到多重背包的基本实现。对于多重背包的基本实现,与完全背包是基本一样的,不同就在于物品的个数上界不再是v/c[i]而是n[i]与v/c[i]中较小的那个。所以我们要在完全背包的基本实现之上,再考虑这个上界问题。
![]()
代码实现如下所示,代码与完全背包的区别除了多了个表示物品个数的数组n[ ]之外,只在内循环的控制条件那里。
-
// 多重背包的基本实现
-
-
public
class MultipleTest {
-
public static void main(String[] args) {
-
int[] w = {
0,
10,
3,
4,
5};
-
int[] v = {
0,
3,
4,
6,
7};
-
//第i个物品对应的个数
-
int[] mount = {
0,
5,
1,
2,
1};
-
int m =
10;
-
int n =
4;
-
int[][] maxValue =
new
int[
5][
16];
-
-
for (
int i=
1; i<=n; i++) {
-
for (
int j=
0; j<=m; j++) {
-
if (i >
1) {
-
maxValue[i][j] = maxValue[i-
1][j];
-
if (j/w[i] >=
1) {
-
int maxTmp =
0;
-
//for (int k=1; k<=j/w[i]; k++) {
-
//多重背包与完全背包的区别只在内循环这里
-
for (
int k=
1; k<=j/w[i] && k<=mount[i]; k++) {
-
if (maxValue[i-
1][j-k*w[i]] + k*v[i] > maxTmp) {
-
maxTmp = maxValue[i-
1][j-k*w[i]] + k*v[i];
-
}
-
}
-
maxValue[i][j] = max(maxValue[i][j], maxTmp);
-
}
-
}
else {
-
if (j/w[
1] >=
1) {
-
maxValue[
1][j] = j/w[
1] * v[
1];
-
}
-
}
-
}
-
}
-
-
System.out.println(
"4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[n][m]);
-
System.out.println();
-
-
// 打印背包的不同承重量
-
System.out.print(
" " +
"\t");
-
for (
int i=
0; i<=m; i++) {
-
System.out.print(i +
"\t");
-
}
-
System.out.println();
-
-
// 打印01背包算法 得到的状态矩阵值
-
for (
int i=
1; i<=n; i++) {
-
System.out.print(
"i="+ i +
"\t");
-
for (
int j=
0; j<=m; j++) {
-
System.out.print(maxValue[i][j]+
"\t");
-
}
-
System.out.println();
-
}
-
}
-
-
public static int max(int a, int b) {
-
if (a > b) {
-
return a;
-
}
-
return b;
-
}
-
}
运行结果如下所示,

2、时间优化(通过二进制拆分转化为01背包问题)
待续
3、优先队列实现
待续
四、小结
本质上,完全背包是多重背包的一个特例:当n[i]都大于等于 V / c[i] 时,多重背包就变为完全背包问题了;01背包是完全背包的一个特例:当第i种物品由可以取0,1,2,...件变为只能取0,1件时(也就是从V / c[i] + 1 种状态 变为 2种状态),完全背包就变为01背包问题了。三者两两之间的关系有点像集合之间的包含关系。
<li class="tool-item tool-active is-like "><a href="javascript:;"><svg class="icon" aria-hidden="true"> <use xmlns:xlink="http://www.w3.org/1999/xlink" xlink:href="#csdnc-thumbsup"></use> </svg><span class="name">点赞</span> <span class="count">10</span> </a></li> <li class="tool-item tool-active is-collection "><a href="javascript:;" data-report-click="{"mod":"popu_824"}"><svg class="icon" aria-hidden="true"> <use xmlns:xlink="http://www.w3.org/1999/xlink" xlink:href="#icon-csdnc-Collection-G"></use> </svg><span class="name">收藏</span></a></li> <li class="tool-item tool-active is-share"><a href="javascript:;"><svg class="icon" aria-hidden="true"> <use xmlns:xlink="http://www.w3.org/1999/xlink" xlink:href="#icon-csdnc-fenxiang"></use> </svg>分享</a></li> <!--打赏开始--> <!--打赏结束--> <li class="tool-item tool-more"> <a> <svg t="1575545411852" class="icon" viewBox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="5717" xmlns:xlink="http://www.w3.org/1999/xlink" width="200" height="200"><defs><style type="text/css"></style></defs><path d="M179.176 499.222m-113.245 0a113.245 113.245 0 1 0 226.49 0 113.245 113.245 0 1 0-226.49 0Z" p-id="5718"></path><path d="M509.684 499.222m-113.245 0a113.245 113.245 0 1 0 226.49 0 113.245 113.245 0 1 0-226.49 0Z" p-id="5719"></path><path d="M846.175 499.222m-113.245 0a113.245 113.245 0 1 0 226.49 0 113.245 113.245 0 1 0-226.49 0Z" p-id="5720"></path></svg> </a> <ul class="more-box"> <li class="item"><a class="article-report">文章举报</a></li> </ul> </li> </ul> </div> </div> <div class="person-messagebox"> <div class="left-message"><a href="https://blog.csdn.net/sinat_30973431"> <img src="https://profile.csdnimg.cn/F/B/3/3_sinat_30973431" class="avatar_pic" username="sinat_30973431"> <img src="https://g.csdnimg.cn/static/user-reg-year/1x/4.png" class="user-years"> </a></div> <div class="middle-message"> <div class="title"><span class="tit"><a href="https://blog.csdn.net/sinat_30973431" data-report-click="{"mod":"popu_379"}" target="_blank">JeremyChan1887</a></span> </div> <div class="text"><span>发布了73 篇原创文章</span> · <span>获赞 30</span> · <span>访问量 3万+</span></div> </div> <div class="right-message"> <a href="https://im.csdn.net/im/main.html?userName=sinat_30973431" target="_blank" class="btn btn-sm btn-red-hollow bt-button personal-letter">私信 </a> <a class="btn btn-sm bt-button personal-watch" data-report-click="{"mod":"popu_379"}">关注</a> </div> </div> </div>






















 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








