隐马尔科夫模型中的Forward-backward算法和java的实现

最新推荐文章于 2020-08-21 15:34:45 发布

原创最新推荐文章于 2020-08-21 15:34:45 发布

· 5.2k 阅读

2 ·

版权

文章标签：

#HMM #forward-backward算法 #自然语言处理

机器学习同时被 2 个专栏收录

4 篇文章

订阅专栏

自然语言处理

4 篇文章

订阅专栏

理论知识

实现这个算法的时候遇到很多困难，因为当时连输入是什么，输出是什么都不知道。而且很多人把forward-backward算法和baum-welch两个算法等同起来了。所以我想先整理一下一些理论的知识。

HMM三个基本问题

在给定的模型中 $\mathbf{\lambda (A,B,\pi)}$ ，然后有一个观测序列 $\mathbf{O = O_{1}O_{2}O_{3}\cdots O_{T}}$ ,预测 $\mathbf{P(O|\lambda)}$ 。就是在这个模型之下，这个序列发生的概率，这个问题是用forward算法或者是backward算法解决的。
在给定的模型 $\mathbf{\lambda (A,B,\pi)}$ 和观测序列 $\mathbf{O = O_{1}O_{2}O_{3}\cdots O_{T}}$ ，寻求隐藏在这个观测序列的最有可能的隐藏状态序列，比如说就是 $\mathbf{Q=Q_{1}Q_{2}Q_{3}\cdots Q_{T}}$ 。这个问题由Viterbi算法解决，上一篇文章中用R语言实现了。
只有观测序列 $\mathbf{O = O_{1}O_{2}O_{3}\cdots O_{T}}$ ，对模型参数 $\mathbf{\lambda (A,B,\pi)}$ 进行估计，这个问题最难也是最复杂的，由Baum-Welch算法解决了，这个算法里面用到的两个子算法就是EM算法和forward-backward算法。

Forward-Backward算法

Forward-Backward算法实际是用来解决Posterior marginal Probability这个问题的，什么是边缘概率。简单来说Forward-backward算法可以求解两种概率分布，但是这个算法得出的结果都是局部最优而不是全局最优。(输入是有参数模型和一个序列，输出下面说明)

第一种就是，在这个输入的观测序列中的某个特定的位置求解这个位置下最有可能的隐含状态。 $P(k|x_{t})$ 就代表在序列的第t个位置，状态为第k个状态的可能性。

第二种就是，同样在这个序列的某个特定位置t下，求这个位置的隐含状态为p，下一个位置的隐含状态为q的概率。 $P(S_{t}=p,S_{t+1}=q|x_{t},\lambda)$ 就是表示在第t个位置，隐含状态为p而下一个状态为q的概率。

Forward-Backward顾名思义就是要有前向变量(Forward Variable或者Forward Probability)和后向变量(Backward Variable)。

前向变量： $\alpha_{t}(p)$ 表示 $\alpha_{t}(p)=P(O_{1},O_{2},O_{3}\cdots O_{t},q_{t}=S_{i}|\lambda)$ 就是序列O的前t个观测序列为 $O_{1}$ 到 $O_{t}$ 并且第t个位置的隐含状态为 $S_{i}$ 的概率。

后向变量： $\beta _{t}(i)$ 表示 $\beta _{t}(i)=P(O_{t+1}O_{t+2}\cdots O_{T}|q_{t}=S_{i},\lambda)$ 就是序列O的后面的观测序列是 $O_{t+1}$ 到 $O_{T}$ 并且第t个位置的隐含状态是 $S_{i}$ 的概率。

前向变量的计算

两个变量的计算其实都是通过动态规划的方法去计算的。假设每一句话是有T个词语，然后总的状态集里面有N个状态。

这里不用说了解的应该知道 $\pi (i)$ 表示模型中第i个状态的作为一个序列中开始的那个词的概率。

$a_{ij}$ 表示从第i个状态转移到第j个状态的概率。

$b_{i}(O)$ 表示第i个状态输出O这个词的概率。

这三个参数构成HMM的模型。

(1)前向变量初始化： $\alpha _{1}(i) = \pi (i)\times b_{i}(O_{1})\: \: \: \: \: \: \: 1 \leq i \leq N$

(2)递推方程： $\alpha _{t+1}(j)=\left [ \sum_{i=1}^{N}\alpha _{t}(i)a_{ij} \right ]b_{j}(O_{t+1}) \: \: \: \: 1\leq t\leq T-1,1\leq j\leq N$

图形解释方程意义，这里本来想自己用Visio画图的，但是感觉没什么时间了。我就直接引用论文上的图了哈~~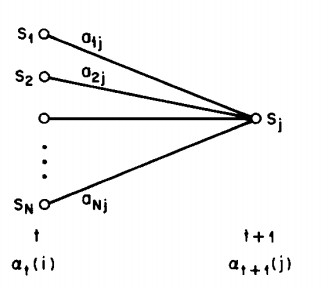

可以看到每一个递推出来的前向变量都是所有前一个时间点的所有状态的前向变量的叠加，因为我们不是明确知道这个时间点的是由前面哪个状态过来的，所以我们需要叠加全部，所以每个时间点的任意状态，都能包括前面时间点的所有状态。

后向变量的计算

(1) 后向变量初始化： $\beta _{T}(i)=1\: \: \: \: 1\leq i\leq N$

(2) 后向变量递推过程： $\beta _{t}(i)=\sum_{j=1}^{N}a_{ij}b_{j}(O_{t+1})\beta _{t+1}(j)\: \: \: t=T-1,T-2,\cdots ,1,\: \:1\leq i\leq N$

图形解释：

同理的是，这个变量从后往前推，包含了后面的变量的所有状态的概率和。当计算到第t个位置为状态 $S_{i}$ 时，必须考虑到在t+1时刻的所有状态的概率，以及他们的输出概率和每一个状态转到 $S_{i}$ 的转移概率。

计算某一点的概率

$\gamma _{t}(i)=P(q_{t}=S_{i}|O,\lambda)$ 我们用 $\gamma _{t}(i)$ 来表示在这个句子的第t个词或者第t个时刻的隐含状态为 $S_{i}$ 的概率。可以证明

$\gamma _{t}(i)=\frac{\alpha _{t}(i)\beta _{i}(i)}{\sum_{i=1}^{N}\alpha _{t}(i)\beta _{i}(i)}$

证明：

$P(q_{t}=S_{i}|O)=\frac{P(q_{t}=S_{i},O)}{P(O)}$

$=\frac{P(O_{1},O_{2},O_{3},\cdots ,O_{t},q_{t}=S_{i})\times P(O_{t+1},O_{t+2},\cdots ,O_{T}|q_{t}=Si)}{P(O)}$

$=\frac{\alpha_{t}(i)\beta_{t}(i)}{P(O)}$

$P(O)=\sum_{i=1}^{N}P(O_{1},O{2},\cdots ,O_{t},\cdots ,O_{T},q_{t}=S_{i})$

$=\sum_{i=1}^{N}P(O_{1},O_{2},\cdots ,O_{t},q_{t}=S_{i})\times P(O_{t+1},O_{t+2},\cdots ,O_{T}|q_{t}=S_{i})$

$=\sum_{i=1}^{N}\alpha_{t}(i)\beta_{t}(i)$

$\rightarrow \gamma_{t}(i)=\frac {\alpha_{t}(i)\beta_{t}(i)}{\sum_{i=1}^{N}\alpha_{t}(i)\beta_{t}(i)}$

证明结束

总结

所以最后得到的结果 $\gamma_{t}(i)$ 就是Forward-backward算法可以得到的其中一个结果，另外一个结果其实也是非常容易得到，同样是用前向变量和后向变量按照上面证明的办法推倒就可以得到Tutorial论文上的概率公式。这个得到的概率明显是局部最优的概率，和上一篇文章用Viterbi算法求得的可以得到整个sentence的隐含状态有区别，因为那个算法是全局最优的。

JAVA实现Forward-Backward算法

首先说明一点，这里用的HMM模型还是上一篇文章的直接简单计算估计的参数模型。所以参数计算部分就不详解了，就直接用了。有问题可以pm我或者email哈~~。这里也不介绍整个程序，只会去介绍一些核心的代码。还有数据集和上一篇文章的viterbi算法也是一样的。

Forward-Backward类的成员变量

因为代码要给老师看，希望大家不介意我的注释用英文

public double[][] transitionProb;		//Transition Probability Matrix
public double[][] emissionProb;			//Emission Probability Matrix
public double[] startProb;				//Start State Probability Matrix
public double[][] alpha;				//Forward Variable
public double[][] beta;					//Backward Variable
public double[][] gamma;				//The distribution of the probability of a specific position
	
public List
    
    
     
      stList;		//List of Train data
public List
     
     
      
       tagList;			//List of tags in train data
public List
      
      
       
        symbolList;			//List of symbols in train data
public List
       
       
        
         oneSequence;	//Just contains one sequence for test the algorithm

Forward变量计算

这里到往下的所有代码都是和我的推导过程一致的，初始化也是。因为感觉和推导过程一样，这里就没必要标注释了哈~~

	public void calculateForwardVariable(){
		for(int t=0;t
     
     
      < code>

 
    
    
 
   
 Backward变量计算 
    
    	public void calculateBackwardVariable(){
		for(int t=oneSequence.size()-1;t>=0;t--){
			for(int i=0;i
      
      
       < code>
       
   
 
     
     
 
    
 Gamma的计算(就是某一点的状态概率分布计算) 
     
      
      	public void calculateGamma(){
		
		for(int t=0;t
        
        
         < code>
         
      
      
       
       
 
      
 结果显示
 最后如果想得到结果，就可以遍历在第t行的每一个i得到每一行最大的概率对应的那个状态，这个状态就是这个点最可能的隐形状态。下面给出显示结果的代码。然后可以把这个结果和测试集的代码的隐含状态对比。得到你的Recall 和 Precision. 
    
 
      
       
       	public void getProbableTag(){
		
		for(int i=0;i
         
         
          
          maxvalue){
					maxvalue = gamma[i][j];
					finalTag = tagList.get(j);
				}
			}
			System.out.println(finalTag);
		}
	}

         
          
       
       
       
 
       
      参考 
      
        最后HMM这部分，建议大家真的可以去看看Tutorial那篇文章。我这里也顺便给出连接。不知道校外的能不能看到论文，whatever，找不到的就找我好了。 
       
       
       A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition

 
   
     Finally, thank you for reading this blog again. Please feel free to contact me if you have any questions.