数据结构与算法之二叉搜索树

最新推荐文章于 2022-07-30 11:38:21 发布

蘑菇蘑菇不会开花~

最新推荐文章于 2022-07-30 11:38:21 发布

阅读量635

点赞数

分类专栏：算法（JAVA）文章标签： Java 算法二叉树 BST

本文链接：https://blog.csdn.net/allen202/article/details/119052513

版权

算法（JAVA）专栏收录该内容

6 篇文章 1 订阅

订阅专栏

一、定义和特性

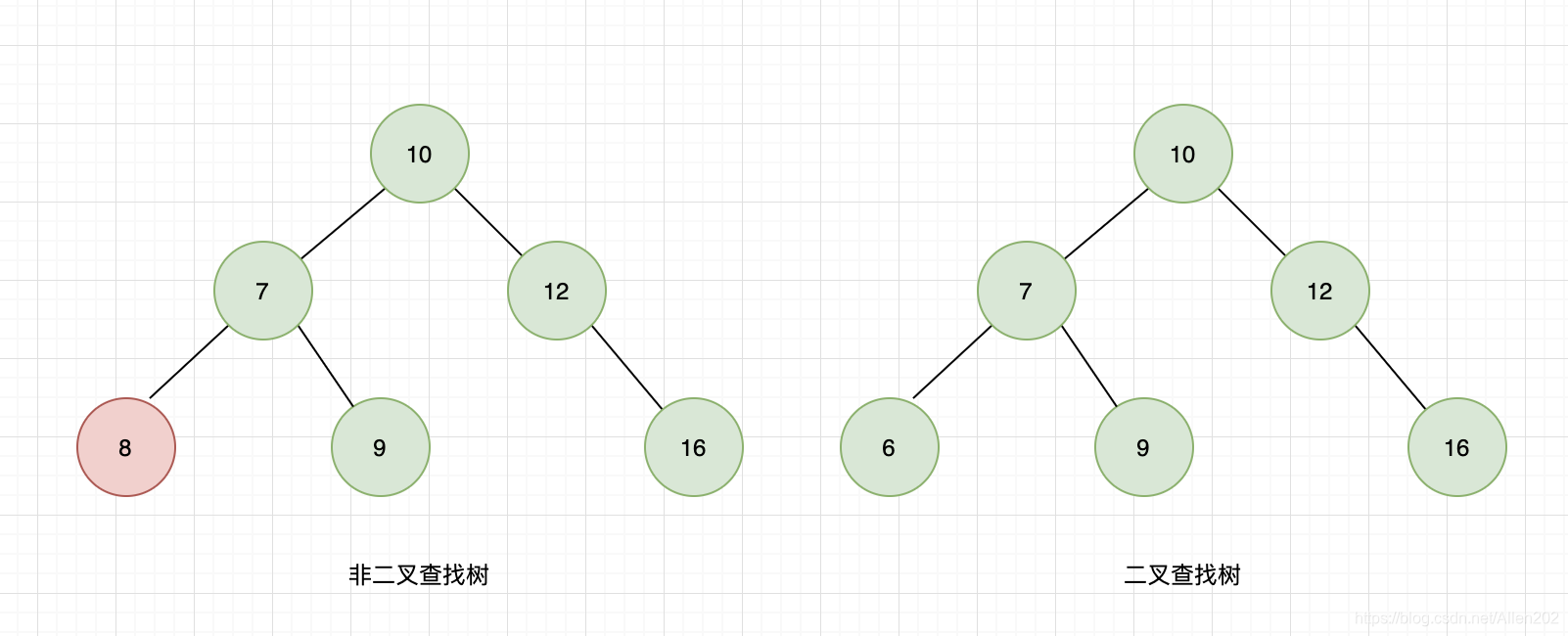
二叉查找树（BST：Binary Search Tree）是一种特殊的二叉树，它改善了二叉树节点查找的效率。二叉查找树有以下性质：

若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
左、右子树也分别为二叉排序树；

代码：

/**
 * 树结点
 */
public static class BSTNode{
    int key;
    BSTNode left;
    BSTNode right;
    BSTNode parent;
    private BSTNode(int key){
        this.key = key;
    }
    public void print(){
        System.out.print(" "+this.key);
    }
}

二、复杂度

2.1 查找复杂度

观察二叉搜索树结构可知，查询每个节点需要的比较次数为节点深度加一。如深度为 0，节点值为 “10” 的根节点，只需要一次比较即可；深度为 1，节点值为 “7” 的节点，只需要两次比较。即二叉树节点个数确定的情况下，整颗树的高度越低，节点的查询复杂度越低。

2.1.1两种极端情况

完全二叉树

完全二叉树，所有节点尽量填满树的每一层，上一层填满后还有剩余节点的话，则由左向右尽量填满下一层。如下图所示，即为一颗完全二叉树；
完美二叉树中树的深度与节点个数的关系为： $n=2^{d+1}-1$ 。设深度为 d 的完全二叉树节点总数为： $n_c$ 。因为完全二叉树中深度为 d 的叶子节点层不一定填满，所以有 $n_c \le 2^{d+1}-1$ ，即： $\ge log_2{(n_c+1)}$ ，因为 d+1 为查找次数，所以完全二叉树中查找次数为 $\lceil log_2{(n_c+1)} \rceil$ 。

单节点

每一层只有一个节点的二叉树，如下图所示
树中每层只有一个节点，该状态的树结构更倾向于一种线性结构，节点的查询类似于数组的遍历，查询复杂度为 $O (n)$ 。所以二叉搜索树的查询复杂度为 $O(log_2 n)~O(n)$
在这里插入图片描述

2.1.2 前序遍历

若二叉树非空，则执行以下操作：

访问根结点；
先序遍历左子树；
先序遍历右子树；
代码如下：

private void preOrder(BSTNode<T> node) {
    if(node != null) {
        System.out.print(node.key+" ");
        preOrder(node.left);
        preOrder(node.right);
    }
}

2.1.3 中序遍历

若二叉树非空，则执行以下操作：

中序遍历左子树；
访问根结点；
中序遍历右子树。
代码如下

private void inOrder(BSTNode<T> node) {
    if(node != null) {
        inOrder(node.left);
        System.out.print(node.key+" ");
        inOrder(node.right);
    }
}

2.1.4 后续遍历

若二叉树非空，则执行以下操作：

后序遍历左子树；
后序遍历右子树；
访问根结点。
代码如下：

private void postOrder(BSTNode<T> node) {
    if(node != null)
    {
        postOrder(node.left);
        postOrder(node.right);
        System.out.print(node.key+" ");
    }
}

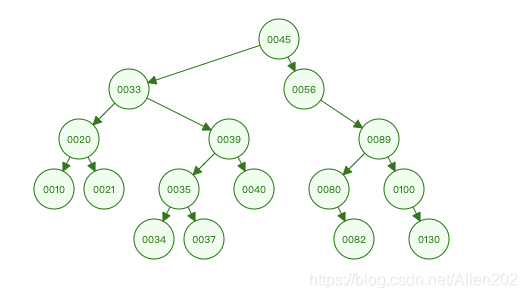
如下图所示，整棵树遍历方式：
前序遍历： 45 33 20 10 21 39 35 34 37 40 56 89 80 82 100 130
中序遍历： 10 20 21 33 34 35 37 39 40 45 56 80 82 89 100 130
后序遍历： 10 21 20 34 37 35 40 39 33 82 80 130 100 89 56 45
在这里插入图片描述

2.1.5 查找一个节点

private BSTNode find(int key){
    BSTNode current;
    current = root;
    while(current != null){
        if(key < current.key){
            current = current.left;
        }else if(key > current.key){
            current = current.right;
        }else{
            return current;
        }
    }
    return null;
}

2.2 构造复杂度

二叉搜索树的构造过程，也就是将节点不断插入到树中适当位置的过程。该操作过程，与查询节点元素的操作基本相同，不同之处在于：

查询节点过程是，比较元素值是否相等，相等则返回，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，返回节点不存在
插入节点的过程是，比较元素值是否相等，相等则返回，表示已存在，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，则将节点插入该空节点位置。
由此可知，单个节点的构造复杂度和查询复杂度相同，为 $O(log_2 n)~O(n)$ ，代码如下：

public void insert(int key){
    BSTNode node = new BSTNode(key);
    BSTNode current = new BSTNode(key);
    if(root == null){
        current.parent = null;
        root = current;
        return;
    }
    current = root;
    while(true){
        if(key >= current.key){
            if(current.right == null){
                current.right = node;
                current.right.parent = current;
                //找到插入位置就插入，并且返回不再执行
                return;
            }else{
                current = current.right;
            }
        }else{
            if(current.left == null){
                current.left = node;
                current.left.parent = current;
                //找到插入位置就插入，并且返回不再执行
                return;
            }else{
                current = current.left;
            }
        }
    }
}

2.3 删除复杂度

二叉搜索树的节点删除包括两个过程，查找和删除。查询的过程和查询复杂度已知，这里说明一下删除节点的过程。

节点的删除有以下三种情况：

待删除节点度为零；
待删除节点度为一；
待删除节点度为二。

第一种情况如下图所示，待删除节点值为 “130”，该节点无子树，删除后并不影响二叉搜索树的结构特性，可以直接删除。

if(node.left == null && node.right == null){
    //若该结点是根结点
    if(parent == null){
        this.root = null;
        return;
    }
    if(parent.left == node){
        parent.left = null;
    }else{
        parent.right = null;
    }
    //若该结点的左子树不空
}

第二种情况：只有一个子节点，如下图所示，待删除节点值为 “80”，该节点有一个左子树，删除节点后，为了维持二叉搜索树结构特性，需要将左子树“上移”到删除的节点位置上。即二叉搜索树中待删除的节点度为一时，可以将待删除节点的左子树或右子树“上移”到删除节点位置上，以此来满足二叉搜索树的结构特性。代码如下：

else if(node.right == null ){
    if(parent.left == node){
        parent.left = node.left;
    }else{
        parent.right = node.left;
    }
}else if(node.left == null ){
    if(parent.left == node){
        parent.left = node.right;
    }else{
        parent.right = node.right;
    }
}

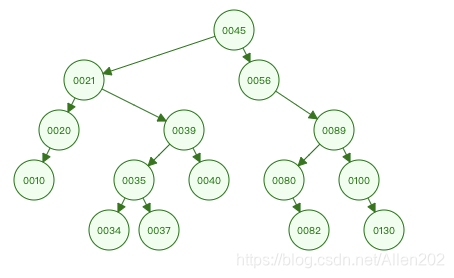
第三种左右左右子结点均不为空。情况如下图所示，待删除节点值为 “33”，该节点既有左子树，也有右子树，删除节点后，为了维持二叉搜索树的结构特性，需要从其左子树中选出一个最大值的节点，“上移”到删除的节点位置上。
这种情况最为复杂，又细分为两种情况：

找出左子树中最大或者右子树中最小的值val；
将当前节点的值替换为val；
在左子树或者右子树中找到val删除
代码如下:

else if(node.left != null && node.right != null){
    //挑选左子树中最大的或者右子树中最小的，替换当前节点，再将替换的节点置空
    int maxKey = findMaxInLeftTree(node.left);
    remove(maxKey);
    node.key = maxKey;
}

在这里插入图片描述

三、完整代码

public class BSTree{
    public BSTNode root;
    /**
     * 树结点
     */
    public static class BSTNode{
        int key;
        BSTNode left;
        BSTNode right;
        BSTNode parent;
        private BSTNode(int key){
            this.key = key;
        }
        public void print(){
            System.out.print(" "+this.key);
        }
    }

    public static void main(String[] args) {
        BSTree bsTree = new BSTree();
        bsTree.insert(45);
        bsTree.insert(33);
        bsTree.insert(56);
        bsTree.insert(20);
        bsTree.insert(39);
        bsTree.insert(89);
        bsTree.insert(10);
        bsTree.insert(21);
        bsTree.insert(35);
        bsTree.insert(40);
        bsTree.insert(80);
        bsTree.insert(100);
        bsTree.insert(34);
        bsTree.insert(37);
        bsTree.insert(82);
        bsTree.insert(130);

        System.out.print("前序遍历：");
        bsTree.preOrder(bsTree.root);
        System.out.println("");
        System.out.print("中序遍历：");
        bsTree.inOrder(bsTree.root);

        System.out.println("");
        System.out.print("后序遍历：");
        bsTree.postOrder(bsTree.root);

        System.out.println("");
        System.out.print("移除130之后的前序(无叶子)：");
        bsTree.remove(130);
        bsTree.preOrder(bsTree.root);

        System.out.println("");
        System.out.print("移除80之后的前序(只有右叶子)：");
        bsTree.remove(80);
        bsTree.preOrder(bsTree.root);

        System.out.println("");
        System.out.print("移除33之后的前序(左右叶子)：");
        bsTree.remove(33);
        bsTree.preOrder(bsTree.root);
    }

    private BSTNode find(int key){
        BSTNode current;
        current = root;
        while(current != null){
            if(key < current.key){
                current = current.left;
            }else if(key > current.key){
                current = current.right;
            }else{
                return current;
            }
        }
        return null;
    }

    public void insert(int key){
        BSTNode node = new BSTNode(key);
        BSTNode current = new BSTNode(key);
        if(root == null){
            current.parent = null;
            root = current;
            return;
        }
        current = root;
        while(true){
            if(key >= current.key){
                if(current.right == null){
                    current.right = node;
                    current.right.parent = current;
                    //找到插入位置就插入，并且返回不再执行
                    return;
                }else{
                    current = current.right;
                }
            }else{
                if(current.left == null){
                    current.left = node;
                    current.left.parent = current;
                    //找到插入位置就插入，并且返回不再执行
                    return;
                }else{
                    current = current.left;
                }
            }
        }
    }

    /**
     * 前序
     */
    private void preOrder(BSTNode node) {
        if(node != null) {
            node.print();
            preOrder(node.left);
            preOrder(node.right);
        }
    }

    /**
     * 中序
     */
    private void inOrder(BSTNode node) {
        if(node != null) {
            inOrder(node.left);
            node.print();
            inOrder(node.right);
        }
    }

    /**
     * 后续
     */
    private void postOrder(BSTNode node) {
        if(node != null)
        {
            postOrder(node.left);
            postOrder(node.right);
            node.print();
        }
    }

    private void remove(int key){
        BSTNode node = find(key);
        if(node == null){
            return;
        }
        BSTNode parent = node.parent;
        //若该结点是叶子结点
        if(node.left == null && node.right == null){
            //若该结点是根结点
            if(parent == null){
                this.root = null;
                return;
            }
            if(parent.left == node){
                parent.left = null;
            }else{
                parent.right = null;
            }
            //若该结点的左子树不空
        }else if(node.right == null ){
            if(parent.left == node){
                parent.left = node.left;
            }else{
                parent.right = node.left;
            }
            //若该结点的右子树不空
        }else if(node.left == null ){
            if(parent.left == node){
                parent.left = node.right;
            }else{
                parent.right = node.right;
            }
        }else if(node.left != null && node.right != null){
            //挑选左子树中最大的或者右子树中最小的，替换当前节点，再将替换的节点置空
            int maxKey = findMaxInLeftTree(node.left);
            remove(maxKey);
            node.key = maxKey;
        }

    }

    //找到左子树中最大的值
    private int findMaxInLeftTree(BSTNode left) {
        if(left == null){
            return 0;
        }
        if(left.right == null){
            return left.key;
        }
        if(left.right == null && left.left == null){
            return left.key;
        }
        return findMaxInLeftTree(left.right);
    }

结果：
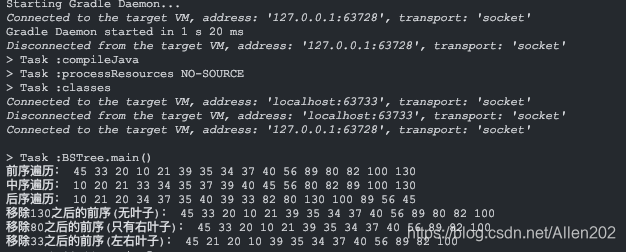
在这里插入图片描述
二叉搜索数演示网站推荐：https://www.cs.usfca.edu/~galles/visualization/BST.html

蘑菇蘑菇不会开花~

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
数据结构与算法之二叉搜索树

目录一、定义和特性二、复杂度2.1 查找复杂度2.1.1两种极端情况完全二叉树单节点2.1.2 前序遍历2.1.3 中序遍历2.1.4 后续遍历2.1.5 查找一个节点2.2 构造复杂度2.3 删除复杂度三、完整代码一、定义和特性二叉查找树（BST：Binary Search Tree）是一种特殊的二叉树，它改善了二叉树节点查找的效率。二叉查找树有以下性质：若左子树不空，则左子树上所有节点的值均小于它的根节点的值；若右子树不空，则右子树上所有节点的值均大于它的根节点的值；左、右子树也分别为二叉排
复制链接

扫一扫