MATLAB滑动T检验

用MATLAB做滑动T检验

滑动t检验是通过考察两组样本平均值的差异是否显著来检验突变。
基本思想是：把一气候序列中两段子序列均值有无显著差异看作来自两个总体均值有无显著差异的问题来检验。如果两段子序列的均值差异超过了一定的显著性水平，则可以认为有突变发生。
本篇博客中的程序1比较结构性比较差，比较乱，程序2的可读性更好
嘿嘿，第一个程序是我自己编的，有很大改进空间，第二个程序是老师给的，方便改参数，直接copy就能用，真香。

程序1

clear all;close all;clc
%% data read
data = xlsread('Tair.xlsx');
time  = data(:,1);
m_sst = data(:,2);
%%    
step_1 = 10;step_2 = 10;%设置两组子序列的步长
length_1 = length(time);%变量的命名不能跟函数名相同，不然再次使用该函数时会报错
%用三个循环，方便每一个变量的查看，也可以将三个循环整合成一个
x1 = [];ss_1 = [];
%求第一个子序列的平均和方差并放在数组X1和SS_1中
for i = 1:length_1 - step_1 - step_2
    x1_bar = mean(m_sst(i:i+step_1-1));
    a = m_sst(i:i+step_1-1);
    s_1 = 0;
    for j = 1:step_1
        s_1 =  s_1 + (a(j)- x1_bar)^2;%可以直接用sum函数求和
    end
    s_1 = s_1./step_1;
    x1 = cat(1,x1,x1_bar);
    ss_1 = cat(1,ss_1,s_1);%使用cat函数时，不能将拼接的两个变量打乱，否则会得到一个顺序相反或者错乱的数组
end
%求第二个子序列的平均和方差并放在数组X2和SS_2中
x2 = [];ss_2 = [];
for k = 1+step_1:length_1 - step_2
    x2_bar = mean(m_sst(k:k + step_2 - 1));
    a = m_sst(k:k + step_2 - 1);
    x2 = cat(1,x2,x2_bar);
    s_2 = 0;
    for l = 1:step_2
        s_2 = s_2 + (a(l)- x2_bar)^2;
    end
    s_2 = s_2./step_2;
    ss_2 = cat(1,ss_2,s_2);
end
%求滑动t值并拼接成一个矩阵
sss = [];
length_2 = length(x2);
tt = [];
for m = 1:length_2
b = sqrt(((step_1 - 1)*ss_1(m) + (step_2 -1)*ss_2(m))/(step_1+step_2 - 2));
sss = cat(1,b,sss);
t = (x1(m)-x2(m))/(b*sqrt(1/step_1 + 1/step_2));
tt = cat(1,tt,t);
end
length_3 = length(tt);
set(0,'defaultfigurecolor','w');%画布背景设置
set(gcf,'units','normalized','position',[0.25 0.25 0.5 0.5]);
plot(time(step_1 + 1:length_3 + step_1),tt,'linewidth',2);
hold on
ttest = 2.878;% significant level  alpha=0.01;
plot(time(step_1 + 1:length_3 + step_1),zeros(length_3,1),'-.','linewidth',1);
plot(time(step_1 + 1:length_3 + step_1),ttest*ones(length_3,1),':','linewidth',3);% line of the significant level
plot(time(step_1 + 1:length_3 + step_1),-ttest*ones(length_3,1),':','linewidth',3);
H=legend('t','0.01 significant level');% explain
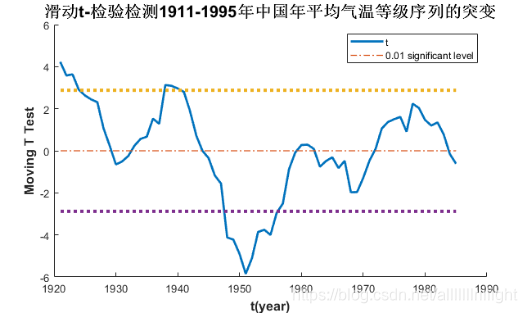
title('滑动t-检验检测1911-1995年中国年平均气温等级序列的突变','fontweight','bold','fontsize',15);
xlabel('t(year)','FontName','TimesNewRoman','FontSize',12,'fontweight','bold');
ylabel('Moving T Test','FontName','TimeNewRoman','FontSize',12,'fontweight','bold');
box off;

结果1

公式

啊，对了，附上滑动T检验的公式，写着写着就忘了

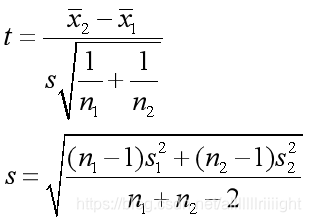
两个子样本的样本长度分别为：n1，n2
均值分别为：
方差分别为：S1,S2

两个滑动子序列
示意图

程序2

clear all;close all;clc
%% 打开数据
f = 'HadISST_sst.nc';
time = ncread(f,'time');
lat  = ncread(f,'latitude');
lon  = ncread(f,'longitude');
sst  = ncread(f,'sst');
%% 将异常值变为NAN
sst(sst == -1000)=NaN;sst(sst == -1.8)=NaN;sst(sst < -1e30) = NaN;
%% 求全球海表平均温度
for t = 1:size(sst,3)
    sst_d    = squeeze(sst(:,:,t));
    m_sst(t) = nanmean(sst_d(:));
end
%m_sst = squeeze(nanmean(squeeze(nanmean(sst,1)),1));
%%    滑动T检验
step = 10; % length of subsequence
v = step+step-2;  % degreee of freedom
ttest = 2.878; % sinnificant level  alpha=0.01;
len1 = step;
len2 = step;
length_1 = length(m_sst);
x = time(step:length_1 - step);
% 将时间序列x变为正常的时间序列
x = x + datenum(1870,01,01);
 
for i = step:length_1 - step
    n1 = m_sst(i-step+1:i);
    n2 = m_sst(i+1:i+step);
    mean1 = mean(n1);
    mean2 = mean(n2);
    c = (len1+len2)/(len1*len2);
    var1 = 1/len1*sum((n1 - mean1).^2);% 直接数组求和
    var2 = 1/len2*sum((n2 - mean2).^2);
    delta1 = (len1-1)*var1 + (len2-1)*var2;
    delta = delta1/(len1 + len2 - 2);
    t(i-step+1) = (mean1 - mean2)/sqrt(delta*c);
end
 
%%    趋势图
figure(1)
set(0,'defaultfigurecolor','w');%画布背景设置
set(gcf,'units','normalized','position',[0.1 0.1 0.8 0.8]);
subplot(2,1,1);
time = double(time);
time = time + datenum(1870,01,01);
plot(time,m_sst,'k-');
datetick('x','mm/dd/yyyy','keepticks');%改时间坐标轴
xlabel('t(year)','FontName','TimesNewRoman','FontSize',12,'fontweight','bold');
ylabel('SST','FontName','TimeNewRoman','FontSize',12,'fontweight','bold');
title('全球海表平均温度时间序列图','fontweight','bold','fontsize',20);
box off;
%%  滑动T检验图
subplot(2,1,2);
plot(x,t,'b-','linewidth',1);
datetick('x','mm/dd/yyyy','keepticks');%改时间坐标轴
xlabel('t(year)','FontName','TimesNewRoman','FontSize',12,'fontweight','bold');
ylabel('Moving T Test','FontName','TimeNewRoman','FontSize',12,'fontweight','bold');
axis([min(x),max(x),-6,6]);% y axis limitation
hold on
plot(x,0*ones(i-step+1,1),'-.','linewidth',1);
plot(x,ttest*ones(i-step+1,1),':','linewidth',3);% line of the significant level
plot(x,-ttest*ones(i-step+1,1),':','linewidth',3);
H=legend('t','0.01 significant level');% explain
title('用滑动T检验检测给出1870.01-2019.12年全球海表平均温度序列的突变','fontweight','bold','fontsize',20);
box off;

结果2