java实现简单的二叉树

二叉排序树,平衡二叉树,红黑树都是在普通二叉树的基础上构建的,所以很有必要学习一下二叉树。

二叉树的遍历:

1:先序遍历(DLR)

  1):访问根节点;

  2):按先序遍历访问左子树

  3):按先序遍历访问右子树

2:中序遍历(LRD)

 1):按中序遍历左子树

 2):访问根节点

 3):按中序遍历访问右子树

3:后序遍历

 1):按后序遍历访问左子树

 2):按后序遍历访问右子树

 3):访问根节点

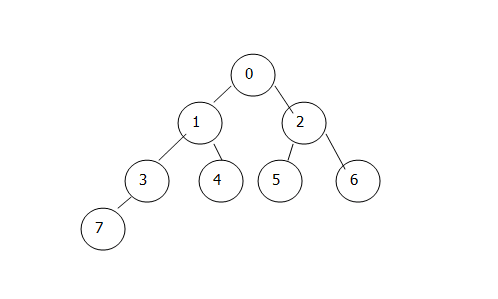
先序遍历的结果为:0  1   3  7  4  2  5  6

中序遍历的结果为:7   3   1  4  0  5  2  6

后序遍历的结果为:7   3   4  1  5  6  2  0

java代码实现:

BinTree类

public class BinTree {
	private BinTree lChild;//左孩子
	private BinTree rChild;//右孩子
	private BinTree root;//根节点
	private Object data; //数据域
	private List<BinTree> datas;//存储所有的节点
	public BinTree(BinTree lChild, BinTree rChild, Object data) {
		super();
		this.lChild = lChild;
		this.rChild = rChild;
		this.data = data;
	}
	public BinTree(Object data) {
		this(null, null, data);
	}
	public BinTree() {
		super();
	}
	
	public void createTree(Object[] objs){
		datas=new ArrayList<BinTree>();
		for (Object object : objs) {
			datas.add(new BinTree(object));
		}
		root=datas.get(0);//将第一个作为根节点
		for (int i = 0; i < objs.length/2; i++) {
			datas.get(i).lChild=datas.get(i*2+1);
			if(i*2+2<datas.size()){//避免偶数的时候 下标越界
				datas.get(i).rChild=datas.get(i*2+2);
			}
		}
	}
	//先序遍历
	public void preorder(BinTree root){
		if(root!=null){
			visit(root.getData());
			preorder(root.lChild);
			preorder(root.rChild);
		}
		
	}
	//中序遍历
	public void inorder(BinTree root){
		if(root!=null){
			inorder(root.lChild);
			visit(root.getData());
			inorder(root.rChild);
		}
		
	}
	//后序遍历
	public void afterorder(BinTree root){
		if(root!=null){
			afterorder(root.lChild);
			afterorder(root.rChild);
			visit(root.getData());
		}
		
	}
	private void visit(Object obj) {
		System.out.print(obj+" ");
	}
	public Object getData() {
		return data;
	}
	public BinTree getRoot() {
		return root;
	}
	
}

测试类:

public class TestTree {
	public static void main(String[] args) {
		BinTree binTree=new BinTree();
		Object[] objs={0,1,2,3,4,5,6,7};
		binTree.createTree(objs);
//		binTree.preorder(binTree.getRoot()); 先序遍历
//		binTree.inorder(binTree.getRoot()); 中序遍历
		binTree.afterorder(binTree.getRoot()); //后序遍历
	}
}