AtCoder Beginner Contest 367（A - C）

传送门

A - Shout Everyday

原题
限制
输入

输出

测试样例

Sample Input 1
21 8 14
Sample Output 1
Yes
Sample Input 2
0 21 7
Sample Output 2
No
Sample Input 3
10 7 17
Sample Output 3
No

题目大意

• 给出三个数A, B, C，Takahashi（后文中统称为甲）在B~C时间段中在睡觉，问在A时刻，甲是否是醒的，若是醒的，则输出Yes,否则输出No,大小写要做区分

分析

• 题目没有说明A,B,C三者间的大小关系，那么就要注意甲有可能是在第一天的B时刻休息，在第二天的C时刻醒来(题目说明了甲的睡眠时间小于24小时)，因此做分类讨论

1.B和C均在同一天，那么就有$B\le C$ 且 $C\le 23$，此时只需要判断A是否在B ~ C时刻间即可，若在B ~ C，甲还在睡觉，则输出No，否则输出Yes

2.B和C不在同一天，那么就有$B\ge C-1$，此时我们可以将A, B, C看作在一个数轴上，将A 和 C都加上24就会变成第一种情况

#include<bits/stdc++.h>
#define all(a) a.begin(), a.end()
using i32 = int;
using u32 = unsigned int;
using i64 = long long;
using u64 = unsigned long long;

//std::mt19937 rng {std::chrono::steady_clock::now().time_since_epoch().count()};

int main() {
	
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);

	int a, b, c;
	std::cin >> a >> b >> c;
	if(b < c) {
		if(a < b || a > c) {
			std::cout << "Yes\n";
		} else {
			std::cout << "No\n";
		}
	} else {
		c += 24;
		a += 24;
		if(a < b || a > c) {
			std::cout << "Yes\n";
		} else {
			std::cout << "No\n";
		}
	}

	return 0;
}

B - Cut .0

原题

限制

输入

输出

测试样例

Sample Input 1
1.012
Sample Output 1
1.012
Sample Input 2
12.340
Sample Output 2
12.34
Sample Input 3
99.900
Sample Output 3
99.9
Sample Input 4
0.000
Sample Output 4
0

题目大意

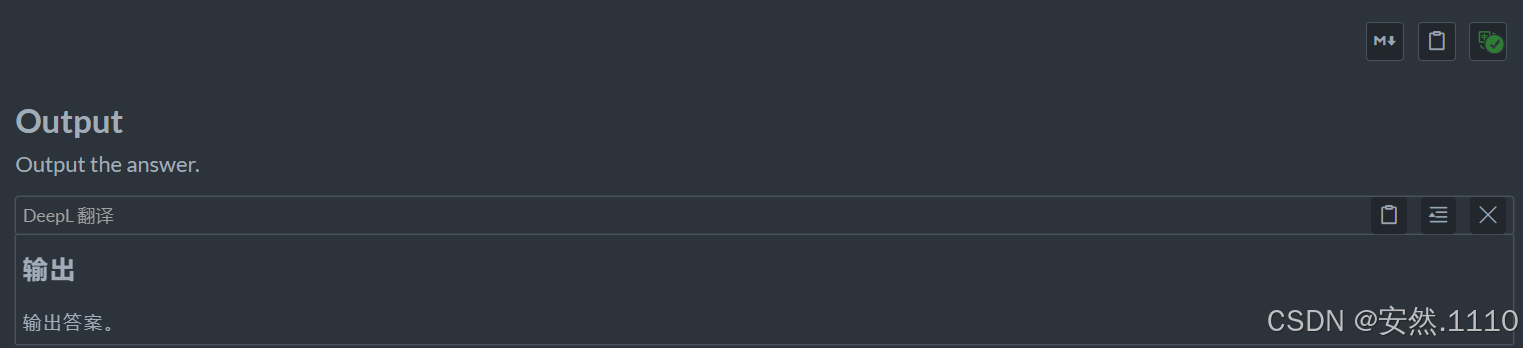
• 给定我们一个浮点数，让我们把小数点末尾的0全部删除，如果全是0，输出整数部分即可

分析

• 如果直接用double类型进行处理，那么是很不方便的，所以我们可以想到用字符串string，这时也要分情况讨论

1.如果小数点后面全是0，那么小数点就不需要打印，只需输出整数部分即可

2.如果小数点后面不全是0，那么只需要输出到不是0的最后一位即可

#include<bits/stdc++.h>
#define all(a) a.begin(), a.end()
using i32 = int;
using u32 = unsigned int;
using i64 = long long;
using u64 = unsigned long long;

//std::mt19937 rng {std::chrono::steady_clock::now().time_since_epoch().count()};

int main() {
	
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);

	std::string x;
	std::cin >> x;
	int n = x.size();
	std::vector<bool> vis(n, true);
	for(int i = n - 1; i >= 0; i--) {
		if(x[i] != '0') {
			break;
		}
		if(x[i] == '0') {
			vis[i] = false;
		}
	}
	int p = x.find('.');
	if(vis[p + 1]) {
		for(int i = 0; i < n; i++) {
			if(vis[i]) {
				std::cout << x[i];
			}
		}
	} else {
		for(int i = 0; i < p; i++) {
			if(vis[i]) {
				std::cout << x[i];
			}
		}
	}
	

	return 0;
}

C - Enumerate Sequences

原题


限制

输入

输出

测试样例

Sample Input 1
3 2
2 1 3
Sample Output 1
1 1 2
2 1 1
2 1 3

Sample Input 2
1 2
1
Sample Output 2
（此处输出为空，没有符合题意的）
Sample Input 3
5 5
2 3 2 3 2
Sample Output 3
1 1 1 1 1
1 2 2 3 2
1 3 1 3 2
1 3 2 2 2
1 3 2 3 1
2 1 2 3 2
2 2 1 3 2
2 2 2 2 2
2 2 2 3 1
2 3 1 2 2
2 3 1 3 1
2 3 2 1 2
2 3 2 2 1

题目大意

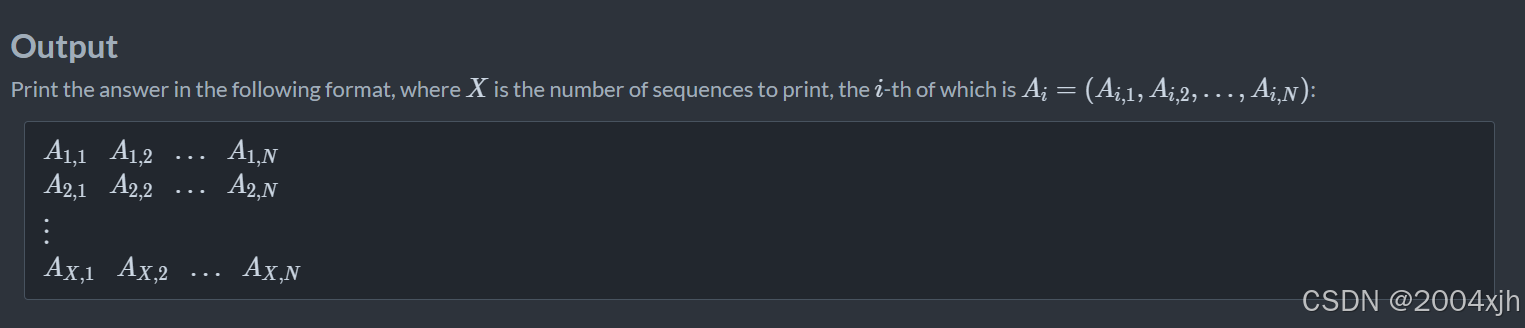
• 给定我们n个数，a1到an，要求我们找到n个数。假设找到的n个元素是{bi1… bn}则且对 $\forall bi\le ai$，找到这些b数组，并按不降序的规则输出

分析

• 由于题给数据比较弱，可以直接暴力搜索这n个数，最多要写8个循环比较累手，所以可以采用dfs来写

1. 暴力搜索

#include<bits/stdc++.h>
#define all(a) a.begin(), a.end()
using i32 = int;
using u32 = unsigned int;
using i64 = long long;
using u64 = unsigned long long;

//std::mt19937 rng {std::chrono::steady_clock::now().time_since_epoch().count()};

int main() {
	
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);

	int n, k;
	std::cin >> n >> k;
	std::vector<int> a(n + 1);
	for(int i = 1; i <= n; i++) {
		std::cin >> a[i];
	}

	if(n == 1) {
		for(int i = 1; i <= a[1]; i++) {
			if(i % k == 0) {
				std::cout << i << "\n";
			}
		}
	} else if(n == 2) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				if((i + j) % k == 0) {
					std::cout << i << " " << j << "\n";
				}
			}
		}
	} else if(n == 3) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				for(int l = 1; l <= a[3]; l++) {
					if((i + j + l) % k == 0) {
						std::cout << i << " " << j << " " 
						<< l << "\n";
					}
				}
			}
		}
	} else if(n == 4) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				for(int l = 1; l <= a[3]; l++) {
					for(int r = 1; r <= a[4]; r++) {
						if((i + j + l + r) % k == 0) {
							std::cout << i << " " << j << " " 
							<< l << " " << r << "\n";
						}
					}
					
				}
			}
		}
	} else if(n == 5) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				for(int l = 1; l <= a[3]; l++) {
					for(int r = 1; r <= a[4]; r++) {
						for(int q = 1; q <= a[5]; q++) {
							if((i + j + l + r + q) % k == 0) {
								std::cout << i << " " << j << " "
								<< l << " " << r << " " << q << "\n";
							}
						}
					}
					
				}
			}
		}
	} else if(n == 6) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				for(int l = 1; l <= a[3]; l++) {
					for(int r = 1; r <= a[4]; r++) {
						for(int q = 1; q <= a[5]; q++) {
							for(int w = 1; w <= a[6]; w++) {
								if((i + j + l + r + q + w) % k == 0) {
									std::cout << i << " " << j << " "
									<< l << " " << r << " " << q << " "
									<< w << "\n";
								}
							}
						}
					}
					
				}
			}
		}
	} else if(n == 7) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				for(int l = 1; l <= a[3]; l++) {
					for(int r = 1; r <= a[4]; r++) {
						for(int q = 1; q <= a[5]; q++) {
							for(int w = 1; w <= a[6]; w++) {
								for(int e = 1; e <= a[7]; e++) {
									if((i + j + l + r + q + w + e) % k == 0) {
										std::cout << i << " " << j << " "
										<< l << " " << r << " " << q << " "
										<< w << " " << e << "\n";
									}
								}
							}
						}
					}
					
				}
			}
		}
	} else if(n == 8) {
		for(int i = 1; i <= a[1]; i++) {
			for(int j = 1; j <= a[2]; j++) {
				for(int l = 1; l <= a[3]; l++) {
					for(int r = 1; r <= a[4]; r++) {
						for(int q = 1; q <= a[5]; q++) {
							for(int w = 1; w <= a[6]; w++) {
								for(int e = 1; e <= a[7]; e++) {
									for(int t = 1; t <= a[8]; t++) {
										if((i + j + l + r + q + w + e + t) % k == 0) {
											std::cout << i << " " << j << " "
											<< l << " " << r << " " << q << " "
											<< w << " " << e << " " << t << "\n";
										}
									}
								}
							}
						}
					}
					
				}
			}
		}
	}
	return 0;
}

2.dfs

#include<bits/stdc++.h>
#define all(a) a.begin(), a.end()
using i32 = int;
using u32 = unsigned int;
using i64 = long long;
using u64 = unsigned long long;

//std::mt19937 rng {std::chrono::steady_clock::now().time_since_epoch().count()};

int main() {
	
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);

	int n, k;
	std::cin >> n >> k;
	std::vector<int> a(n + 1);
	for(int i = 1; i <= n; i++) {
		std::cin >> a[i];
	}
	std::vector<int> temp;

	std::function<void(int)> dfs = [&](int x) -> void {
		if(x > n) {
			int sum = std::accumulate(all(temp), 0);
			if(sum % k == 0) {
				for(auto t : temp) {
					std::cout << t << " ";
				}
				std::cout << "\n";
			}
			return;
		}
		for(int i = 1; i <= a[x]; i++) {
			temp.push_back(i);
			dfs(x + 1);
			temp.pop_back();
		}
	};

	
	dfs(1);

	return 0;
}