机器学习（六）——SVM（4）、学习理论

http://antkillerfarm.github.io/

序列最小优化方法（续）

同理：

$$L-y^{(2)}Lv_2=Lf_2$$

$$f_2=y^{(2)}(b-E_2)+s\alpha_1K_{12}+\alpha_2K_{22}$$

由《机器学习（五）》中的公式5可得：

$$W_L=L_1f_1+Lf_2-\frac{1}{2}L_1^2K_{11}-\frac{1}{2}L^2K_{22}-sLL_1K_{12}$$

$\alpha_2^{new}=H$的情况，同理可得：

$$\alpha_1^{new}=H_1=\alpha_1+s(\alpha_2-H)$$

$$W_H=H_1f_1+Hf_2-\frac{1}{2}H_1^2K_{11}-\frac{1}{2}H^2K_{22}-sHH_1K_{12}$$

根据$W_H$和$W_L$哪个是极值，可以反过来确定$\alpha_2^{new}=L$$，还是$$\alpha_2^{new}=H$。

至此，迭代关系式除了b的推导式以外，都已经推出。

由《机器学习（五）》中的公式8可得：

$$u_1^{new}-b^{new}-y^{(1)}\alpha_1^{new}K_{11}-y^{(2)}\alpha_2^{new}K_{12}=u_1-b-y^{(1)}\alpha_1K_{11}-y^{(2)}\alpha_2K_{12}$$

迭代的目的是使预测更为准确，因此设置$u_1^{new}=y^{(1)}$是很直观的做法，因此：

$$\begin{align} -b^{new}&=u_1-u_1^{new}+y^{(1)}(\alpha_1^{new}-\alpha_1)K_{11}+y^{(2)}(\alpha_2^{new}-\alpha_2)K_{12} \\&=(u_1-y^{(1)})+y^{(1)}(\alpha_1^{new}-\alpha_1)K_{11}+y^{(2)}(\alpha_2^{new}-\alpha_2)K_{12} \\&=E_1+y^{(1)}(\alpha_1^{new}-\alpha_1)K_{11}+y^{(2)}(\alpha_2^{new}-\alpha_2)K_{12} \end{align}$$

上式是根据$u_1$得到的$b^{new}$，我们将之记作$b_1$。

同理，可得：

$$-b_2=E_2+y^{(1)}(\alpha_1^{new}-\alpha_1)K_{12}+y^{(2)}(\alpha_2^{new}-\alpha_2)K_{22}$$

如果$\alpha_1^{new}$在边界内，则$b^{new}=b_1$；如果$\alpha_2^{new}$在边界内，则$b^{new}=b_2$。

如果$\alpha_1^{new}$和$\alpha_2^{new}$都在边界内，则$b^{new}=b_1=b_2$。

如果$\alpha_1^{new}$$和$$\alpha_2^{new}$都在边界上，则$b_1$和$b_2$之间的任意值都满足KKT条件，一般取$b^{new}=\frac{b_1+b_2}{2}$。

SMO算法在线性SVM时的简化

由《机器学习（四）》一节的公式3，可得：

$$w^{new}-y^{(1)}\alpha_1^{new}x^{(1)}-y^{(2)}\alpha_2^{new}x^{(2)}=w-y^{(1)}\alpha_1x^{(1)}-y^{(2)}\alpha_2x^{(2)}$$

$$w^{new}=w+y^{(1)}(\alpha_1^{new}-\alpha_1)x^{(1)}+y^{(2)}(\alpha_2^{new}-\alpha_2)x^{(2)}$$

需要注意的是，虽然我们在之前的讨论中，使用$K_{ij}$代替$\langle x^{(i)},x^{(j)}\rangle$进行扩展，然而两者只有在线性的情况下，才是等价的，即$\phi(x)=x$。

K函数最大的作用不在于计算线性SVM，而在于计算非线性的SVM。

SMO中拉格朗日乘子的启发式选择方法

所谓的启发式选择方法主要思想是每次选择拉格朗日乘子的时候，优先选择$0<\alpha_i<C$的$\alpha_i$作优化，因为边界上的$\alpha_i$在迭代之后通常不会更改。

给定初始值$\alpha_i=0$后，先对所有样例进行循环，循环中碰到违背KKT条件的（不管边界上还是边界内）都进行迭代更新。等这轮过后，如果没有收敛，第二轮就只针对$0<\alpha_i<C$的样例进行迭代更新。

软边距SVM问题的KKT条件为：

$$\alpha_i=0 \Leftrightarrow y^{(i)}u_i\ge 1$$

$$0<\alpha_i<C \Leftrightarrow y^{(i)}u_i=1$$

$$\alpha_i=C \Leftrightarrow y^{(i)}u_i\le 1$$

在第一个乘子选择后，第二个乘子也使用启发式方法选择， 第二个乘子的迭代步长大致正比于$\lvert E_1-E_2\rvert$，选择能使$\lvert E_1-E_2\rvert$最大的$\alpha_2$即可。

最后的收敛条件是在界内（$0<\alpha_i<C$）的样例都能够遵循KKT条件，且其对应的$\alpha_i$只在极小的范围内变动。

学习理论

偏差和方差

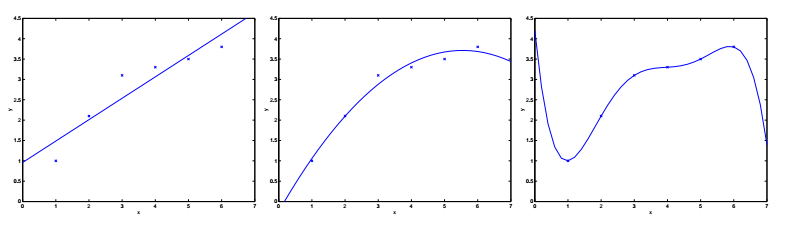
回到之前的欠拟合与过拟合的例子。我们把预测值和实际值之间的误差称为泛化误差。注意：泛化误差不是拟合模型和训练样本值之间的差，后者通常被称作模型误差。

偏差（bias）和方差（variance）都是泛化误差（generalization error）的组成部分。但遗憾的是，这两个名词至今也没有公认的严格定义，这里只做定性的描述，即：欠拟合的误差主要是偏差，而过拟合的误差主要是方差。

学习理论的预备知识

学习理论（learning theory）主要解决三大问题：

1.偏差和方差的权衡。这实际上是模型选择的问题。如何才能自动确定模型的阶数呢？

2.如何关联模型误差和泛化误差？

3.如何确定我们的学习算法是有效的？

首先介绍两个定理：

The union bound定理：

如果$A_1,\dots,A_k$是k个不同的事件，则：

$$P(A_1\cup \dots\cup A_k)\le P(A_1)+\dots+P(A_k)$$

Hoeffding不等式：

$Z_1,\dots,Z_m$是m个独立且具有相同分布的随机变量（independent and identically distributed，IID）。如果它们满足Bernoulli($\phi$)分布，即$P(Z_i=1)=\phi,P(Z_i=0)=1-\phi$，则：

$$P(\lvert\phi-\hat\phi\rvert>\gamma)\le 2\exp(-2\gamma^2m)$$

其中，$\hat\phi=(1/m)\sum_{i=1}^mZ_i$，$\gamma$是大于0的任意常数。

这个不等式是Wassily Hoeffding于1963年证明的。它表明样本数量越大，则随机变量的平均值越接近其数学期望值。

注：Wassily Hoeffding，1914~1991，芬兰统计学家，柏林大学博士，无偏统计学（U-statistics）创始人。

这个不等式在统计学领域也叫做Chernoff bound，但实际上是Herman Chernoff的朋友Herman Rubin发现的。他们的关系有点像苹果公司的那两个Steve，都是统计学领域的巨擘。

注：Herman Chernoff，1923年生，美国数学家、物理学家，布朗大学博士，先后执教于MIT和哈佛。

Herman Rubin，1926年生，美国数学家，21岁获得芝加哥大学的博士学位。现为普渡大学教授。
Herman Chernoff写过一篇文章回忆他和Herman Rubin的友谊，其中提到后者IQ 180，比他牛多了。其实，Herman Chernoff 24岁获得博士学位，也是妥妥的学霸级人物。

以下假定y的取值为0或1，则：

$$\hat\varepsilon(h)=\frac{1}{m}\sum_{i=1}^m1\{h(x^{(i)})\neq y^{(i)}\}$$

$\hat\varepsilon(h)$被称作训练误差（training error），也叫做经验风险（empirical risk）或经验误差（empirical error），它表征的是在训练样本集上，预测函数误分类的比率。

$$\varepsilon(h)=P^{(x,y)~\mathcal{D}}(h(x)\neq y)$$

$\varepsilon(h)$表示泛化误差，$(x,y)$表示被预测的样本，$\mathcal{D}$表示样本所遵循的概率分布。

注意：$\hat\varepsilon(h)$和$\varepsilon(h)$针对的样本集是不同的，后面定义的变量h和$\hat h$也遵循相同的约定。

这里我们假设：训练数据和预测数据都具有相同的概率分布$\mathcal{D}$。这个假设是PAC理论的假设之一。

PAC（Probably approximately correct）理论是Leslie Valiant于1984年提出的。这里的大部分讨论都和PAC有关。

注：Leslie Valiant，1949年生，英国计算机科学家，华威大学博士。哈佛大学教授，英国皇家学会会员，图灵奖获得者（2010）。

对于线性分类$h_\theta(x)=1\{\theta^Tx\ge 0\}$来说，寻找合适的参数$\theta$，还有另一种方法，即最小化训练误差，并令：

$$\hat\theta=\arg\min_\theta\hat\varepsilon(h_\theta)$$

我们将这个过程称为经验风险最小化（empirical risk minimization，ERM）。其最终的预测函数为$\hat h=h_{\hat\theta}$。

ERM是一类基本的学习算法，也是本节关注的焦点。

我们定义预测函数类（hypothesis class ）$\mathcal{H}$，用以表示解决某类学习问题的所有可能的分类器的集合。（实际上也就是参数$\theta$所有可能取值的集合。）则ERM算法可表示为：

$$\hat h=\arg\min_{h\in \mathcal{H}}\hat\varepsilon(h)$$

$\mathcal{H}$为有限集的情况

根据之前的讨论，我们做如下定义：

$$Z=1\{h_i(x)\neq y\}$$

$$Z_j=1\{h_i(x^{(j)})\neq y^{(j)}\}$$

$$\hat\varepsilon(h_i)=\frac{1}{m}\sum_{j=1}^mZ_j$$

其中，$h_i\in \mathcal{H}$。

由Hoeffding不等式可知：

$$P(\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma)\le 2\exp(-2\gamma^2m)$$

这个公式表明：对于特定的$h_i$，在m很大的情况下，训练误差有很大的概率接近于泛化误差。

如果我们用$A_i$表示事件$\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma$，则上式可改为$P(A_i)\le 2\exp(-2\gamma^2m)$。

$$P(\exists h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma)=P(A_1\cup \dots\cup A_k)$$

$$\le \sum_{i=1}^kP(A_i)\le \sum_{i=1}^k2\exp(-2\gamma^2m)=2k\exp(-2\gamma^2m)$$

$$\begin{align} &1-P(\exists h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma)=P(\lnot\exists h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma) \\&=P(\forall h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert\le\gamma)\ge 1-2k\exp(-2\gamma^2m) \end{align}$$

上面的结果表明，对于所有的$h\in \mathcal{H}$，实际上也有一个收敛性质。这个性质被称为一致收敛（uniform convergence）。

上式变形可得：

$$m\ge \frac{1}{2\gamma^2}\log\frac{2k}{\delta}$$

其中，$\delta=2k\exp(-2\gamma^2m)$。

上式表明，在固定$\gamma$和$\delta$的情况下，至少需要多少训练样本，才能保证对于所有的$h\in \mathcal{H}$，$P(\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert\le \gamma)$至少为$1-\delta$。

这里的m也被称为算法的样本复杂度（sample complexity），它表征达到一定性能所需要的训练样本的数量。

同样的，我们固定m和$\delta$，可得：

$$\lvert\varepsilon(h)-\hat\varepsilon(h)\rvert\le \sqrt{\frac{1}{2m}\log\frac{2k}{\delta}}$$

如果我们定义$h^*=\arg\min_{h\in \mathcal{H}}\varepsilon(h)$，则根据一致收敛性质$\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert\le \gamma$可得：

$$\varepsilon(\hat h)\le \hat\varepsilon(\hat h)+\gamma$$

因为$\hat h$已经是$\hat \varepsilon(h)$中最小的一个，因此$\hat\varepsilon(\hat h)\le \hat\varepsilon(h)$对所有都是成立的，其中当然包括$h^*$，即$\hat\varepsilon(\hat h)\le \hat\varepsilon(h^*)$。因此，上式可改为：

$$\varepsilon(\hat h)\le \hat\varepsilon(h^*)+\gamma$$

根据一致收敛性质，我们还可以得出$\hat\varepsilon(h^*)\le \varepsilon(h^*)+\gamma$，因此，上式继续变形为：

$$\varepsilon(\hat h)\le \varepsilon(h^*)+2\gamma$$

这个公式表明，作为ERM结果的$\hat h$，比最好的h，至多只差$2\gamma$。

我们将之前的结果合到一起，可得如下定理：

令$\lvert\mathcal{H}\rvert=k$，并固定$m,\delta$的取值，且一致收敛的概率至少为$1-\delta$，则：

$$\varepsilon(\hat h)\le \left(\min_{h\in \mathcal{H}}\varepsilon(h)\right)+2\sqrt{\frac{1}{2m}\log\frac{2k}{\delta}}$$

假设我们需要从预测函数类$\mathcal{H}$切换到一个更大的预测函数类$\mathcal{H'}\supseteq\mathcal{H}$，则上面公式的第一项只会变得更小，也就是说偏差会变小，但由于k的增加，第二项会变大，也就是方差会变大。

同理，可得以下针对m的定理：

令$\lvert\mathcal{H}\rvert=k$，并固定$\delta,\gamma$的取值，为了保证$\varepsilon(\hat h)\le \left(\min_{h\in \mathcal{H}}\varepsilon(h)\right)+2\gamma$的概率至少为$1-\delta$，则：

$$m\ge \frac{1}{2\gamma^2}\log\frac{2k}{\delta}=O\left(\frac{1}{\gamma^2}\log\frac{k}{\delta}\right)$$