机器学习（九）——EM算法

http://antkillerfarm.github.io/

高斯混合模型和EM算法（续）

E-Step中，根据贝叶斯公式可得：

$$p(z^{(i)}=j\vert x^{(i)};\phi,\mu,\Sigma)=\frac{p(x^{(i)}\vert z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{\sum_{l=1}^kp(x^{(i)}\vert z^{(i)}=l;\mu,\Sigma)p(z^{(i)}=l;\phi)}$$

将假设模型的各概率密度函数代入上式，即可计算得到$w_j^{(i)}$。

相比于K-means算法，GMM算法中的$z^{(i)}$是个概率值，而非确定值，因此也被称为soft assignments。

K-means算法各个聚类的特征都是一样的，也就是“圆圈”的半径一致。而GMM算法的“圆圈”半径可以不同。如下面两图所示：

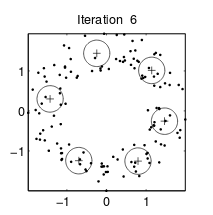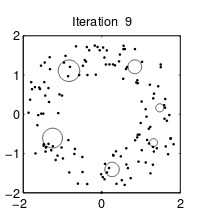K-means算法	GMM算法

GMM算法结果也是局部最优解。对其他参数取不同的初始值进行多次计算同样适用于GMM算法。

参考：

http://cseweb.ucsd.edu/~atsmith/project1_253.pdf

EM算法

本节将进一步讨论EM算法的性质，并将之应用到使用latent random variables的一大类估计问题中。

Jensen不等式

首先我们给出凸函数的定义：

设f是定义域为实数的函数，如果对于所有的实数x，$f''(x)\ge 0$，那么f是凸函数。当x是向量时，如果其Hessian矩阵H是半正定的（$H\ge 0$），那么f是凸函数。如果$f''(x)>0$或$H>0$，那么称f是严格凸函数。

Jensen不等式表述如下:

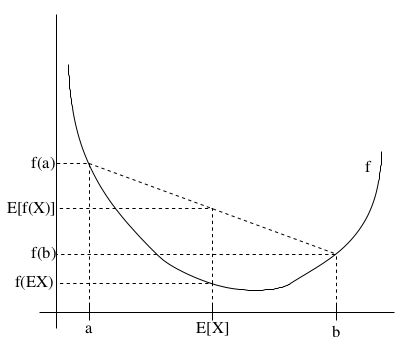
如果f是凸函数，X是随机变量，那么$E[f(X)]\ge f(EX)$。

特别地，如果f是严格凸函数，那么$E[f(X)]=f(EX)$，当且仅当$p(X=EX)=1$。也就是说X是常量。

在不引起误会的情况下，$E[X]$简写做$EX$。

这个不等式的含义如下图所示：

Jensen不等式应用于凹函数时，不等号方向反向，也就是$E[f(X)]\le f(EX)$

注：Johan Ludwig William Valdemar Jensen，1859～1925，丹麦人。主业工程师，副业数学家。

EM算法的一般形式

EM算法一般形式的似然函数为：

$$\ell(\theta)=\sum_{i=1}^m\log p(x^{(i)};\theta)=\sum_{i=1}^m\log \sum_zp(x^{(i)},z^{(i)};\theta)\tag{1}$$

根据这个公式直接求$\theta$一般比较困难，但是如果确定了z之后，求解就容易了。

EM算法是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化$\ell(\theta)$，我们可以不断地建立$\ell(\theta)$的下界(E-Step),然后优化下界(M-Step)。

这里首先假设$z^{(i)}$的分布为$Q_i$。显然：

$$\sum_zQ_i(z)=1,Q_i(z)\ge 0$$

$$\begin{align} \ell(\theta)&=\sum_{i=1}^m\log \sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta) \\&=\sum_{i=1}^m\log \sum_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\&\ge\sum_{i=1}^m\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\tag{2} \end{align}$$

这里解释一下最后一步的不等式变换。

首先，根据数学期望的定义公式：

$$E[X]=\sum_{i=1}^nx_ip_i$$

可知：

$$\sum_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=E\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right]$$

又因为$f(x)=\log x$是凹函数，根据Jensen不等式可得：

$$f\left(E_{z^{(i)}\sim Q_i}\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right]\right)\ge E_{z^{(i)}\sim Q_i}\left[f\left(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right)\right]$$

综上，公式2给出了$\ell(\theta)$的下界。对于$Q_i$的选择，有多种可能，那种更好的？

假设$\theta$已经给定，那么$\ell(\theta)$的值就取决于$Q_i(z^{(i)})$和$p(x^{(i)},z^{(i)})$了。我们可以通过调整这两个概率，使下界不断上升，以逼近$\ell(\theta)$的真实值。当不等式变成等式时，下界达到最大值。

由Jensen不等式相等的条件可知，$\ell(\theta)$的下界达到最大值的条件为：

$$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=c$$

其中c为常数。

这实际上表明：

$$Q_i(z^{(i)})\propto p(x^{(i)},z^{(i)};\theta)$$

其中的$\propto$符号是两者成正比例的意思。

从中还可以推导出：

$$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=c=\frac{\sum_zp(x^{(i)},z^{(i)};\theta)}{\sum_zQ_i(z^{(i)})}$$

因为$\sum_zQ_i(z^{(i)})=1$，所以上式可变形为：

$$Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_zp(x^{(i)},z^{(i)};\theta)}=\frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)}=p(z^{(i)}\vert x^{(i)};\theta)$$

可见，当$Q_i(z^{(i)})$为$z^{(i)}$的后验分布时，$\ell(\theta)$的下界达到最大值。

因此，EM算法的过程为：

Repeat until convergence {
(E-step) For each i：
$Q_i(z^{(i)}):=p(z^{(i)}\vert x^{(i)};\theta)$
(M-step) Update the parameters：
$\theta:=\arg\max_\theta\sum_i\sum_zQ_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$
}

如何保证算法的收敛性呢？

如果我们用$\theta^{(t)}$和$\theta^{(t+1)}$表示EM算法第t次和第t+1次迭代后的结果，那么我们的任务就是证明$\ell(\theta^{(t)})\le \ell(\theta^{(t+1)})$。

由公式1和2可得：

$$\ell(\theta)\ge\sum_i\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\tag{3}$$

由之前的讨论可以看出，E-Step中的步骤是使上式的等号成立的条件，即：

$$\ell(\theta^{(t)})=\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}$$

因为公式3对于任意$Q_i$和$\theta$都成立，因此：

$$\ell(\theta^{(t+1)})\ge\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})}$$

因为M-Step的最大化过程，可得：

$$\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})}\ge\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}$$

综上可得：$\ell(\theta^{(t)})\le \ell(\theta^{(t+1)})$

事实上，如果我们定义：

$$J(Q,\theta)=\sum_i\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

则EM算法可以看作是J函数的坐标上升法。E-Step固定$\theta$，优化Q；M-Step固定Q，优化$\theta$。

重新审视混合高斯模型

下面给出混合高斯模型各参数的推导过程。

E-Step很简单：

$$w_j^{(i)}=Q_i(z^{(i)}=j)=p(z^{(i)}=j\vert x^{(i)};\phi,\mu,\Sigma)$$

在M-Step中，我们将各个变量和分布的概率密度函数代入，可得：

$$\begin{align} &\sum_{i=1}^m\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\&=\sum_{i=1}^m\sum_{j=1}^kQ_i(z^{(i)}=j)\log\frac{p(x^{(i)}\vert z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{Q_i(z^{(i)}=j)} \\&=\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\frac{\frac{1}{(2\pi)^{n/2}\lvert\Sigma_j\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)\right)\cdot \phi_j}{w_j^{(i)}} \end{align}$$

对$\mu_l$求导，可得：

$$\begin{align} &\nabla_{\mu_l}\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\frac{\frac{1}{(2\pi)^{n/2}\lvert\Sigma_j\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)\right)\cdot \phi_j}{w_j^{(i)}} \\&=-\nabla_{\mu_l}\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j) \\&=\frac{1}{2}\sum_{i=1}^mw_l^{(i)}\nabla_{\mu_l}(2\mu_l^T\Sigma_l^{-1}x^{(i)}-\mu_l^T\Sigma_l^{-1}\mu_l)=\sum_{i=1}^mw_l^{(i)}(\Sigma_l^{-1}x^{(i)}-\Sigma_l^{-1}\mu_l)\tag{4} \end{align}$$

这里对最后一步的推导，做一个说明。为了便于以下的讨论，我们引入符号“tr”，该符号表示矩阵的主对角线元素之和，也被叫做矩阵的“迹”（Trace）。按照通常的写法，在不至于误会的情况下，tr后面的括号会被省略。

tr的其他性质还包括：

$$\operatorname{tr}\,a=a,a\in R\tag{5.1}$$

$$\operatorname{tr}(A + B) = \operatorname{tr}(A) + \operatorname{tr}(B)\tag{5.2}$$

$$\operatorname{tr}(cA) = c \operatorname{tr}(A)\tag{5.3}$$

$$\operatorname{tr}(A) = \operatorname{tr}(A^{\mathrm T})\tag{5.4}$$

$$\operatorname{tr}(AB) = \operatorname{tr}(BA)\tag{5.5}$$

$$\operatorname{tr}(ABCD) = \operatorname{tr}(BCDA) = \operatorname{tr}(CDAB) = \operatorname{tr}(DABC)\tag{5.6}$$

$$\nabla_A\operatorname{tr}(AB)=B^T\tag{5.7}$$

$$\nabla_{A^T}f(A)=(\nabla_Af(A))^T\tag{5.8}$$

$$\nabla_A\operatorname{tr}(ABA^TC)=CAB+C^TAB^T\tag{5.9}$$

$$\nabla_{A^T}\operatorname{tr}(ABA^TC)=B^TA^TC^T+BA^TC\tag{5.10}$$

$$\nabla_A|A|=|A|(A^{-1})^T\tag{5.11}$$

因为$\mu_l^T\Sigma_l^{-1}\mu_l$是实数，由公式5.1可得：

$$\nabla_{\mu_l}\mu_l^T\Sigma_l^{-1}\mu_l=\nabla_{\mu_l}\operatorname{tr}(\mu_l^T\Sigma_l^{-1}\mu_l)$$

由公式5.10可得：

$$\nabla_{\mu_l}\operatorname{tr}(\mu_l^T\Sigma_l^{-1}\mu_l)=(\Sigma_l^{-1})^T(\mu_l^T)^TI^T+\Sigma_l^{-1}(\mu_l^T)^TI=(\Sigma_l^{-1})^T\mu_l+\Sigma_l^{-1}\mu_l$$

因为$\Sigma_l^{-1}$是对称矩阵，因此，综上可得：

$$\nabla_{\mu_l}\mu_l^T\Sigma_l^{-1}\mu_l=2\Sigma_l^{-1}\mu_l\tag{5.12}$$

回到正题，令公式4等于0，可得：

$$\mu_j:=\frac{\sum_{i=1}^mw_j^{(i)}x^{(i)}}{\sum_{i=1}^mw_j^{(i)}}$$

同样的，对$\phi_j$求导，可得：

$$\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\phi_j$$

因为存在$\sum_{j=1}^k\phi_j=1$这样的约束，因此需要使用拉格朗日函数：

$$\mathcal{L}(\phi)=\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\phi_j+\beta(\sum_{j=1}^k\phi_j-1)$$

这里的$\beta$是拉格朗日乘子，$\phi_j\ge 0$的约束条件不用考虑，因为对$\log\phi_j$求导已经隐含了这个条件。

因此：

$$\frac{\partial\mathcal{L}(\phi)}{\partial\phi_j}=\sum_{i=1}^m\frac{w_j^{(i)}}{\phi_j}+\beta$$

令上式等于0，可得：

$$\frac{\sum_{i=1}^mw_j^{(i)}}{\phi_j}=-\beta=\frac{\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}}{\sum_{j=1}^k\phi_j}$$

因为$\sum_{j=1}^k\phi_j=1,\sum_{j=1}^kw_j^{(i)}=1$，所以：

$$-\beta=\frac{\sum_{i=1}^m1}{1}=m$$

因此：

$$\phi_j:=\frac{1}{m}\sum_{i=1}^mw_j^{(i)}$$

因子分析

之前的讨论都是基于样本个数m远大于特征数n的，现在来看看$m\ll n$的情况。

这种情况本质上意味着，样本只覆盖了很小一部分的特征空间。当我们应用高斯模型的时候，会发现协方差矩阵$\Sigma$根本就不存在，自然也就没法利用之前的方法了。

那么我们应该怎么办呢？

对$\Sigma$的限制

有两种方法可以对$\Sigma$进行限制。

方法一：

设定$\Sigma$为对角线矩阵，即所有非对角线元素都是0。其对角线元素为：

$$\Sigma_{jj}=\frac{1}{m}\sum_{i=1}^m(x_j^{(i)}-\mu_j)^2$$

二维多元高斯分布在平面上的投影是个椭圆，中心点由$\mu$决定，椭圆的形状由$\Sigma$决定。$\Sigma$如果变成对角阵，就意味着椭圆的两个轴都和坐标轴平行了。

方法二：

还可以进一步约束$\Sigma$，可以假设对角线上的元素都是相等的，即：

$$\Sigma=\sigma^2I$$

其中：

$$\sigma=\frac{1}{mn}\sum_{j=1}^n\sum_{i=1}^m(x_j^{(i)}-\mu_j)^2$$