1003.Max Sum

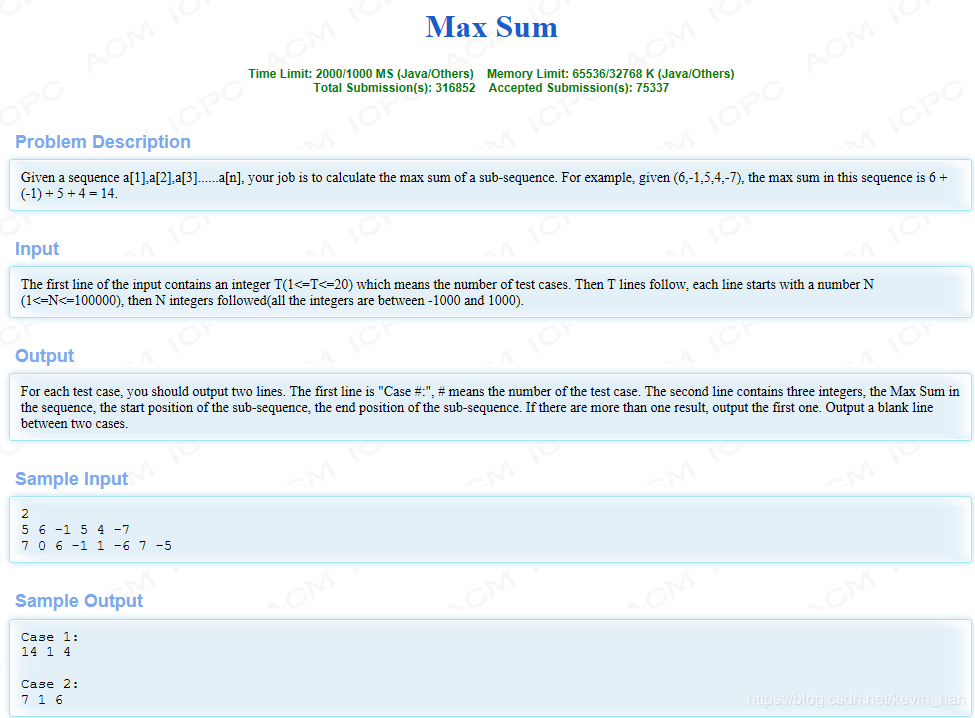
一开始是开了一个二维数组 保存每一个位置所对应的值 结果发现过于啰嗦 而且过于臃肿 导致我出错后一直找不到那里错 所以参考了其他解法 改写原来的方法

import java.util.*;
public class Main {
    public static void main(String[] args) {
        int w = 1;
        int[] arr = new int[100002];//会被覆盖
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        while (n > 0) {
            int num = sc.nextInt();
            // 将数据放进数组中 maxsum 统计最大值 flag 临时最大值
            int maxSum = -9999;
            int flag = 0;//一段数据的极大值 不一定为最大值
            int star = 0;//开始位置 从0 开始
            int end = 0;//结束位置 从0 开始
            int z = 0;//记录正确的位置
            for (int i = 0; i < num; i++) {
                arr[i] = sc.nextInt();// 读取数据 然后进行处理
                flag += arr[i];
                if (flag > maxSum) {
                    maxSum = flag;
                    end = i;
                    star = z;
                }
                if (flag < 0) {// 归零处理 根据判断 此处arr[i]为负数
                    flag = 0;
                    z = i + 1;//z仅在这里修改
                }
            }
            System.out.println("Case "+(w++)+":");
            System.out.println(maxSum+" "+(star+1)+" "+(1+end));
            if (n != 1) 
                System.out.println();
            n--;
        }
    }
}

转载于:https://www.cnblogs.com/cznczai/p/11150156.html