matlab:双或三方演化博弈,lotka-Volterra 1.双方演化博弈:代分析稳定点分析,代绘制相位图,matlab仿真图代码
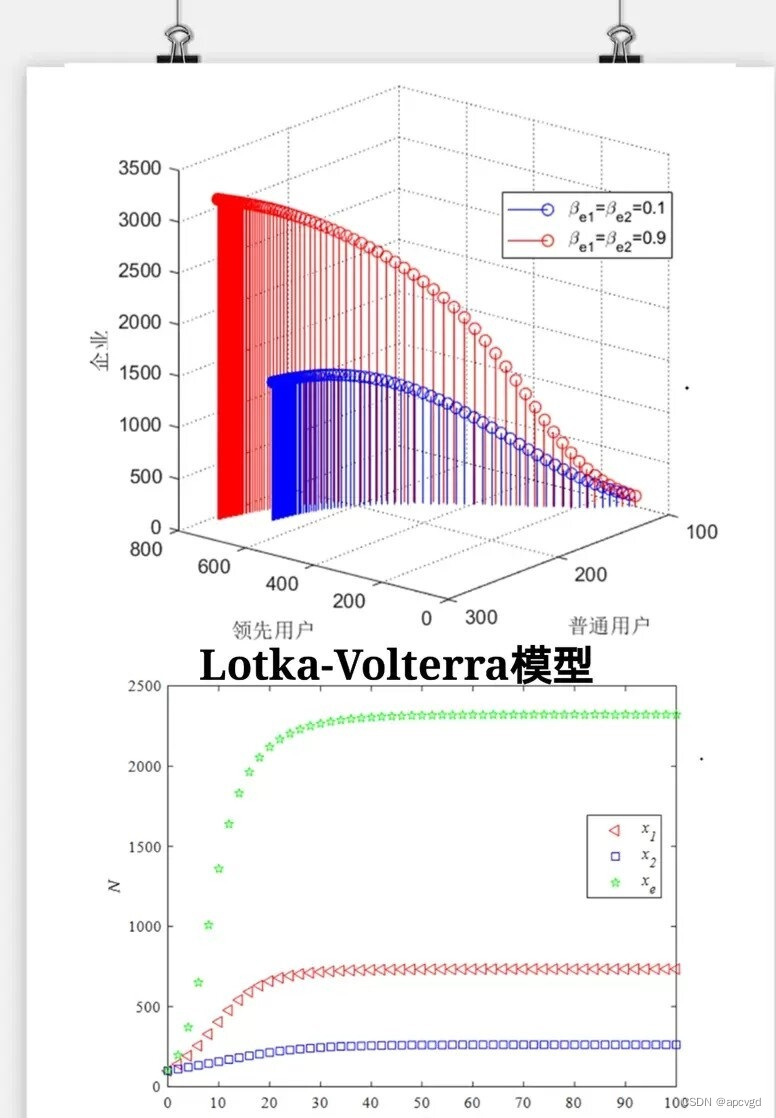
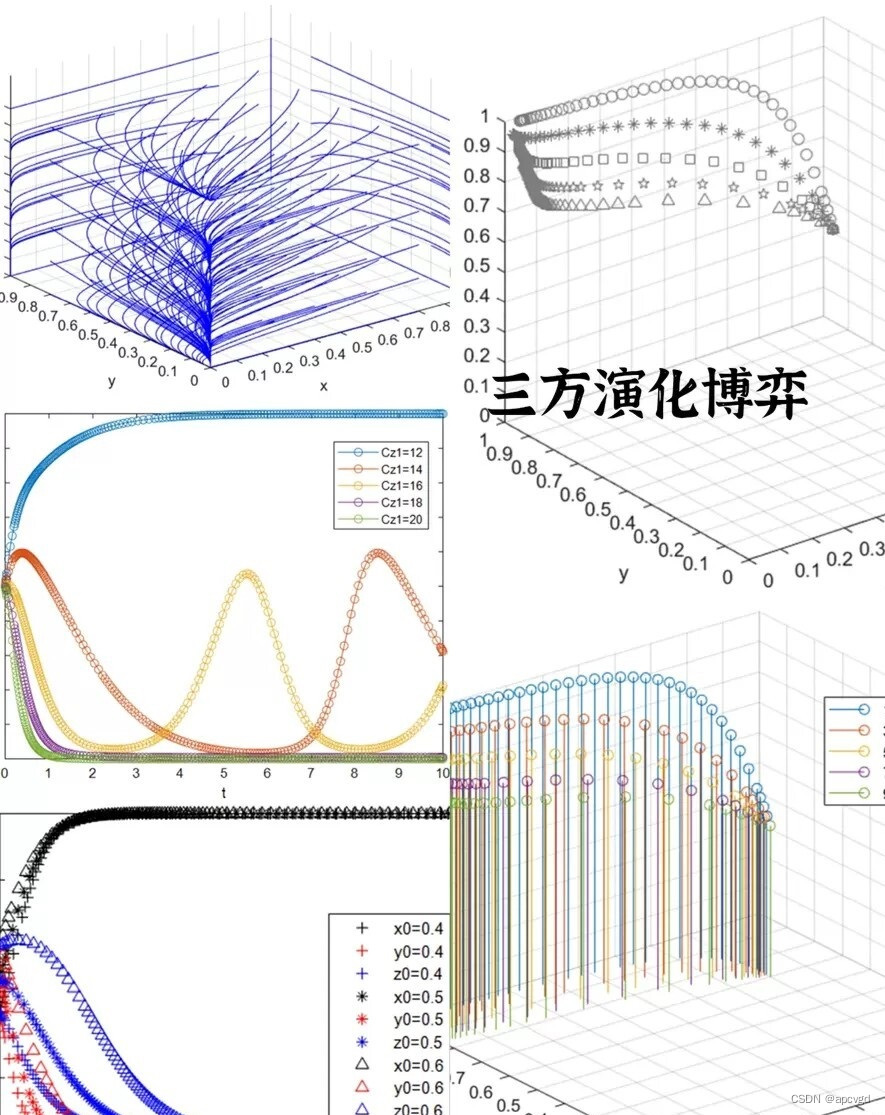
2.三方演化博弈:代分析稳定点分析,代绘制相位图,matlab仿真图代码3.lotka-Volterra模型

YID:7350644023709252
资料来源于 https://www.liruan.net/963.html
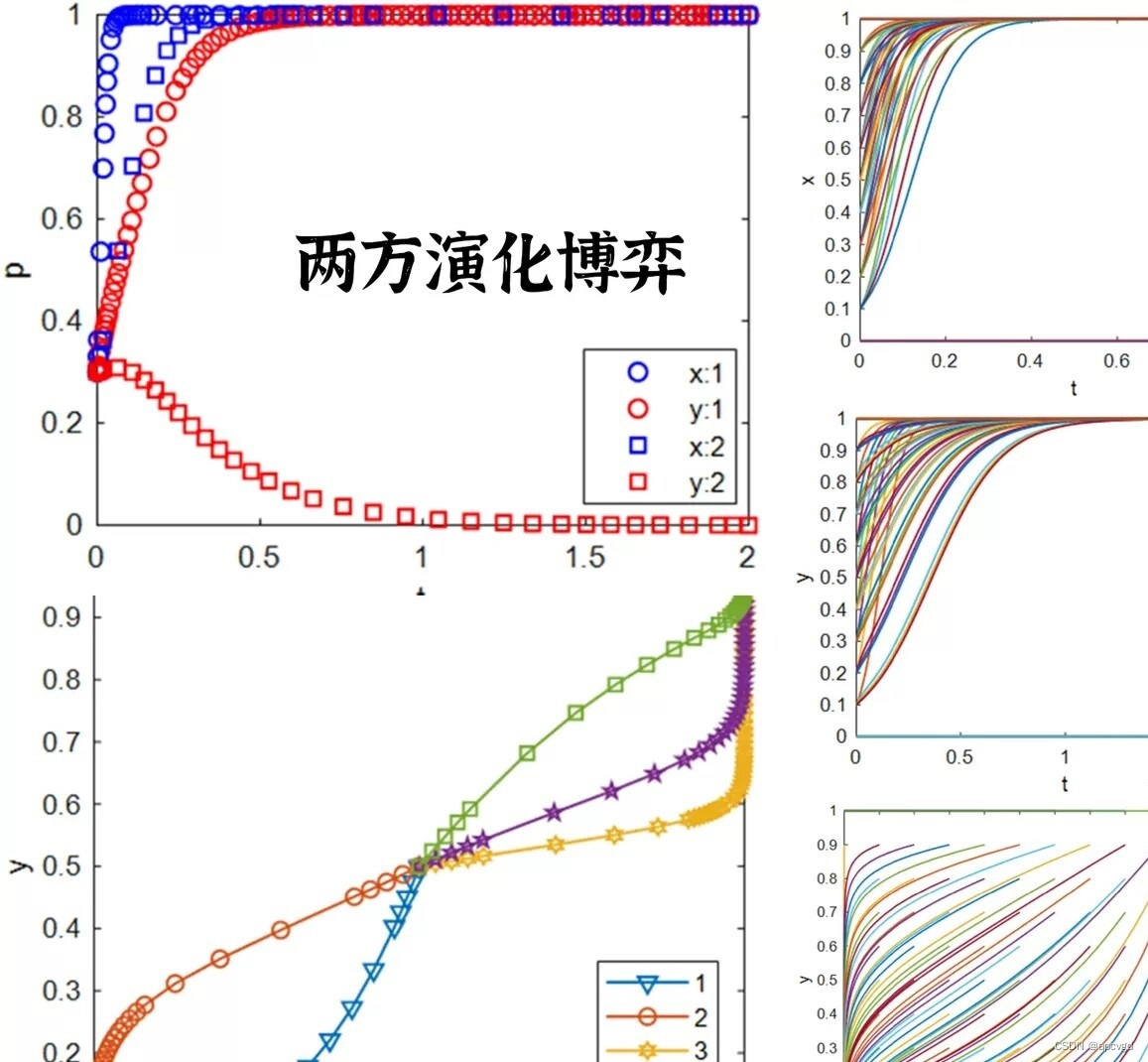
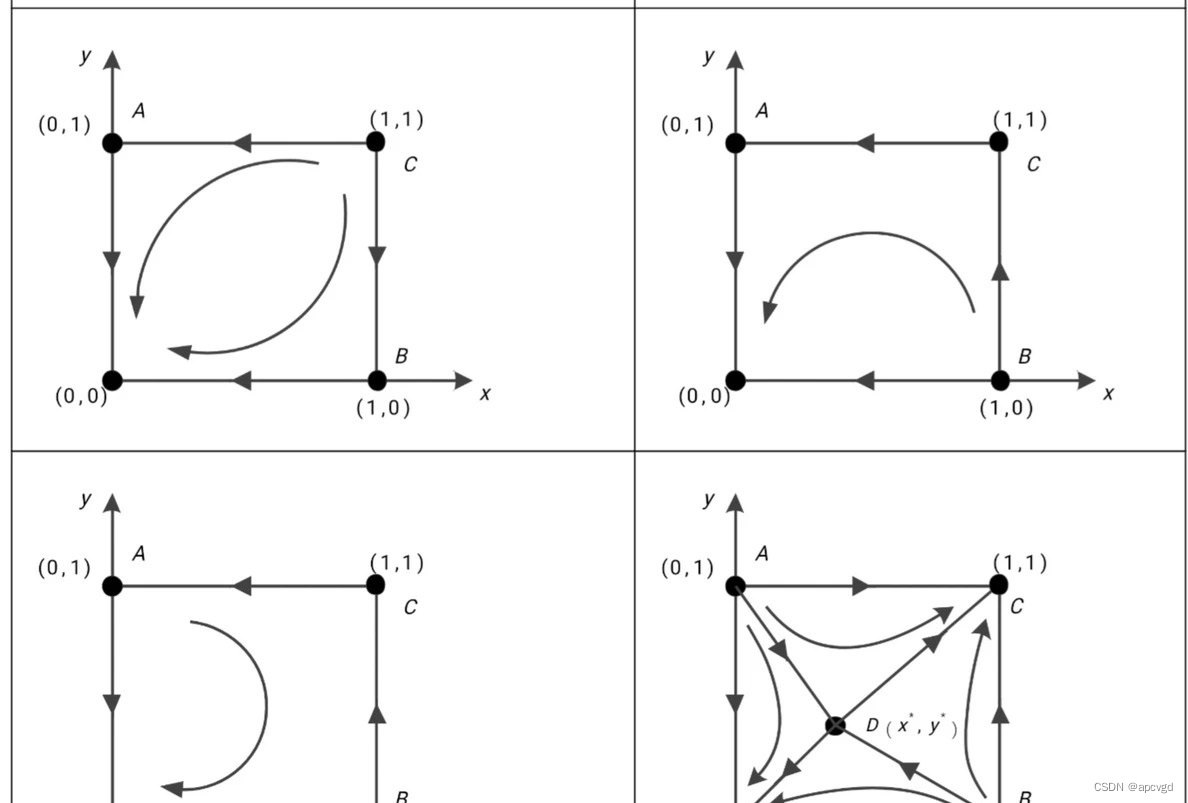
matlab:双或三方演化博弈,lotka-Volterra 1.双方演化博弈:代分析稳定点分析,代绘制相位图,matlab仿真图代码
2.三方演化博弈:代分析稳定点分析,代绘制相位图,matlab仿真图代码3.lotka-Volterra模型

YID:7350644023709252
资料来源于 https://www.liruan.net/963.html




 2596
2596
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


