SVM总结

开始：

给定训练集：

$$T = \{(x_1,y_1),(x_2,y_2),(x_3,y_3),...,(x_n,y_n)\}$$ ，其中 $x_i \in x=R^n$， $y_i \in y = \{+1,-1\}$, $i=1,2,...,N$

定义：

函数间隔

超平面(w,b)关于样本点$(x_i,y_i)$ 的函数间隔为：

$$\hat{\gamma_i} = y_i(w \cdot x_i + b)$$
超平面(w,b)关于训练集T的函数间隔为：
$$\hat{\gamma} = \min_{i=1,...,N}\hat \gamma_i$$
增加约束，使||w|| = 1，这时函数间隔称为几何间隔。

几何间隔

超平面(w,b)关于样本点$(x_i,y_i)$的几何间隔：

$$\hat{\gamma_i} = y_i({\frac {w }{||w||} }\cdot x_i + {\frac {b }{||w||} })$$
超平面(w,b)关于训练集T的几何间隔为：
$$\hat{\gamma} = \min_{i=1,...,N}\hat \gamma_i$$

1.线性可分

几何间隔最大化的分离超平面：

$$w^*\cdot x + b^* = 0$$
相应的分类决策函数：
$$f(x) = sign(w^*\cdot x + b)$$

$$\Longrightarrow$$ 转化为优化问题：
$$\max_{w,b}\gamma_{几何}$$
$$s.t. \quad y_i({\frac {w }{||w||} }\cdot x_i + {\frac {b }{||w||}})\geq \gamma, i=1,2,...,N$$
由几何间隔和函数间隔的关系 $\Longrightarrow$
$$\max_{w,b}\frac{\gamma_{函数}} {||w||}$$
$$s.t. \quad \ y_i (w\cdot x_i + b)\geq \gamma_{函数}, i=1,2,...,N$$
可以取 $\hat \gamma_{函数}=1$
$$\Longrightarrow$$
$$s.t.\quad \ y_i (w\cdot x_i + b-1)\geq 0, i=1,2,...,N$$
就推出了 凸二次规划的形式。

插入知识点：1.凸优化

$$\min_w f(w)$$
$$s.t. \quad g_i(w)\leq0, i=1,2,...,k$$
$$s.t. \quad h_i(w)=0, i=1,2,...,l$$
其中，目标函数f(w)和约束函数 $g_i(w)$都是 $R^n$上连续可微的凸函数，约束函数 $h_i(w)$是 $R^n$上的仿射函数。

2.拉格朗日对偶性

对于上面的凸优化问题，引入拉格朗日函数：

$$L(x,\alpha,\beta)=f(x)+\sum_{i=1}^k \alpha_ig_i(x) + \sum_{j=1}^l \beta_jh_j(x)$$
其中 $\alpha_i,\beta_i$是拉格朗日乘子， $\alpha_i\geq0$
设 $\theta_p(x)=\max_{\alpha,\beta;\alpha_i\geq0}L(x,\alpha,\beta)$
则，若x违反原始问题约束，则可以取 $\alpha \rightarrow +\infty$或者取 $\beta \rightarrow +\infty$，因此针对这些情况 $\theta_p(x)$为正无穷。相反的，若x遵循原始问题的约束，那么无论 $\alpha,\theta$如何取值，由于乘以0，最后都是0，于是 $\theta_p(x)=f(x)$。
$$于是有\Longrightarrow$$
$$\theta_p(x)=\left\{ \begin{aligned} f(x),\quad x满足原始问题约束 \\ +\infty，\quad 其他 \end{aligned} \right.$$
$$\min_x\theta_p(x)=\min_x max_{\alpha,\beta;\alpha_j\geq0} L(x,\alpha,\beta)$$
与原问题等价。
原始问题和对偶问题：
$$\max \min L(x,\alpha,\beta)\leq\min\max L(x,\alpha,\beta)$$
特别的，对于凸优化问题，等式成立的充要条件是KKT条件。

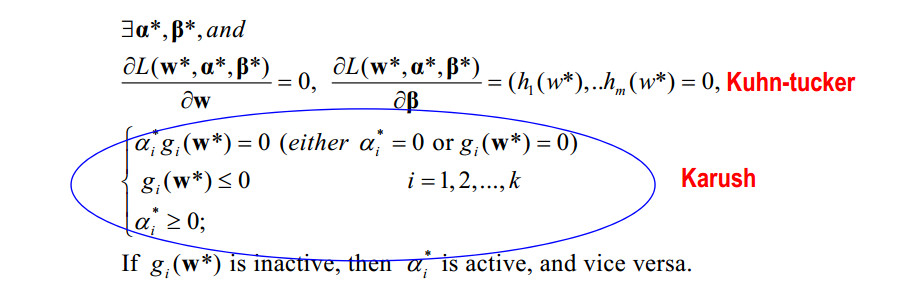
继续：

根据刚才补充的知识，凸二次问题等价于拉格朗日对偶问题（满足KKT条件）。

$$L(w,\alpha,\beta)=\frac1 2||w||^2-\sum_{i=1}^N\alpha_iy_i(w\cdot x_i+b)+\sum_{i=1}^{N}\alpha_i$$
其中， $\alpha = (\alpha_1,\alpha_2,...,\alpha_N)^T$是拉格朗日乘子向量。
原始问题： $\max \min L(x,\alpha,\beta)$
对偶问题： $\min \max L(x,\alpha,\beta)$

(1)求$\min_{w,b}L(w,b,\alpha)$

$$\frac{\partial L}{\partial w} =w-\sum_{i=1}^N\alpha_iy_ix_i=0$$
$$\Longrightarrow w = \sum_{i=1}^{N}\alpha_iy_ix_i$$
$$\frac{\partial L}{\partial b} =\sum_{i=1}^N\alpha_iy_i=0$$
$$\Longrightarrow \sum_{i=1}^{N}\alpha_iy_i=0$$
上面两个推论代入，得
$$L(w,b,\alpha)=\frac1 2 \sum_{i=1}^{N} \sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i$$