Stata：嵌套Logit模型(NestedLogit)

原文链接：https://www.lianxh.cn/news/d5e00bfb17a7c.html

致谢： 这篇推文的核心内容主要来自陈强老师编著的《高级计量经济学及 Stata 应用》一书，特此致谢。

 

 

1. 简介

此前，连享会发布了一系列离散选择模型相关的推文，参见 连享会 - 离散选择模型专题，本文介绍一种相对复杂的模型 —— 嵌套 Logit 模型。

多元 Logit 模型需满足 IIA (Independent of Irrelevant Alternatives) 的假设，即无关选择枝之间是相互独立的。但这个假设有时是难以满足的，这样就会导致错误的结果。例如交通方式选择中 “红蓝巴士” 的经典问题。该问题描述了如下交通方式选择的情形：

假设出行者有两种交通方式可供选择：小汽车 (car) 和红色公交车 (red bus)，选择枝方案集记为 。假设这两种交通方式的效用值  是相等的，则选择小汽车与红色公交车的概率为：

现在，新增了一种蓝色公交车 (blue bus) 的选择枝，这三种交通方式构成的方案集记为 。并且，蓝色公交车除了颜色与红色公交车不同之外，其本质是相同的，则三种交通方式的效用值为：

那么，根据多元 Logit 模型的计算公式，选择这三种交通方式的概率为：

显然，这个概率的结果是错误的。因为除了颜色不同之外，蓝色与红色公交车的本质是相同的，不会由于公交车的颜色不同而影响出行者选择公交车方式或者小汽车方式出行。导致这个错误的原因是三个选择枝之间是不独立的，即蓝色公交车与红色公交车具有相关性，这就违背了 IIA 假设。

此时，可以采用将具有相关的选择枝 (红色与蓝色公交车) 归到一个组，允许同组内的选择枝相关，但不同组之间要相互独立。出行者选择交通方式时先在各个组之间 (公交车与小汽车) 进行选择，再选择组内的交通方式 (红色与蓝色公交车) ，形成树状或嵌套 (nested) 的结构，如下图 1 所示：

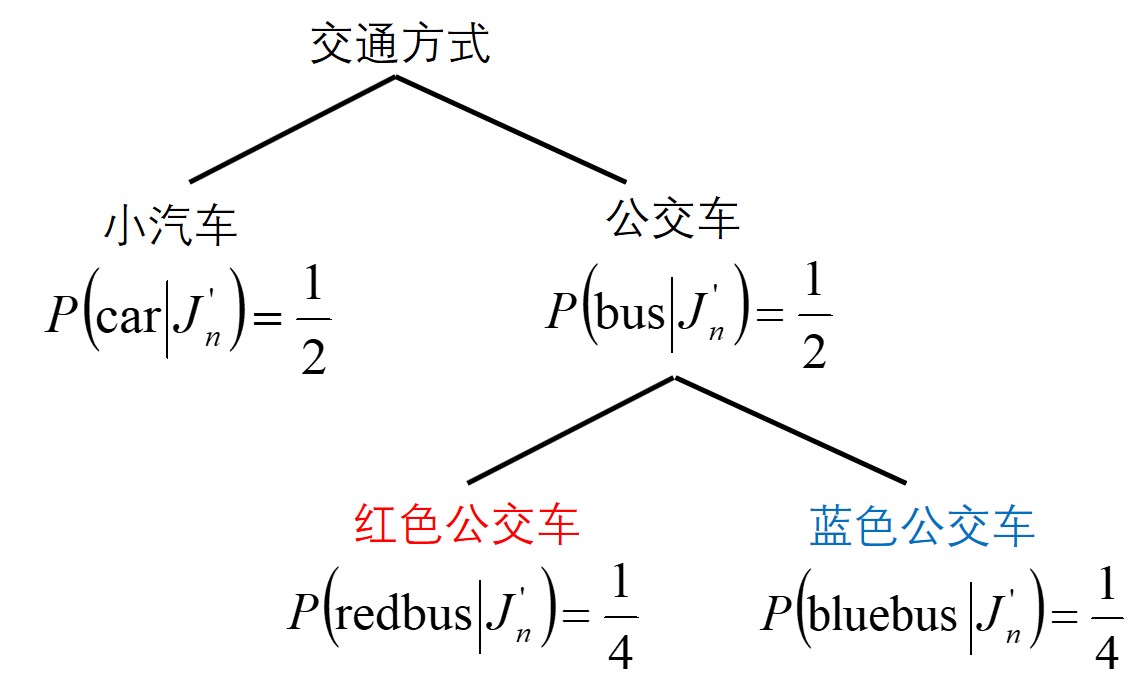图 1 交通方式选择的树状或嵌套结构

在此情形下，选择小汽车、红色公交车与蓝色公交车的正确概率为：

 

原文链接：https://www.lianxh.cn/news/d5e00bfb17a7c.html