转载至:http://blog.sina.com.cn/s/blog_6a2e0c8801015378.html
内积空间
在数学上,内积空间是增添了一个额外的结构的矢量空间。这个额外的结构叫做内积或标量积。这个增添的结构将一对矢量与一个纯量连接起来,允许我们严格地谈论矢量的“夹角”和“长度”,并进一步谈论矢量的正交性。内积空间由欧几里得空间抽象而来(内积是点积的抽象),这是泛函分析讨论的课题。
关于内积空间的例子,请参看希尔伯特空间。
内积空间有时也叫做准希尔伯特空间(pre-Hilbert Space),因为由内积定义的距离完备化之后就会得到一个希尔伯特空间。
在早期的著作中,内积空间被称作酉空间,但这个词现在已经被淘汰了。在将内积空间称为酉空间的著作中,“内积空间”常指任意维(可数/不可数)的欧几里德空间。
定义
域F上的一个内积空间V备有一个正定、非退化以及共轭双线性形式,称作内积(F是[[实数域]]时,内积是一个正定、对称、非退化以及双线性形式):
满足以下公理:
- 共轭对称;
-
这个设定蕴含着
 对于所有
对于所有
 , 因为
, 因为
 .
.
-
(共轭也写成加星号:
 ,如同共轭转置。)
,如同共轭转置。)
- 对第一个元素是线性算子;
-
由前两条可以得到:
-
因此  实际上是一个半双线性形式。
实际上是一个半双线性形式。
- 非负性:
-
-
-
(这样就定义了
 对于所有
对于所有  。说明内积是从点积抽象而来。)
。说明内积是从点积抽象而来。)
- 非退化:
在有限维的矢量空间中,只需要验证它是单射。
-
-
 当且仅当
当且仅当
 。
。
-
- 因此,内积空间是一个 Hermitian形式 。
V 满足可加性:
-
对所有的
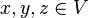 ,
,
 ,
,

如果F是实数域R那么共轭对称性质就是对称性。
共轭双线性变成了一般的双线性。
备注。多数数学家要求内积在第一个参数上是线性的而在第二个参数上是共轭线性的,本文接受这种约定。很多物理学家接受相反的约定。这种改变是非实质性的,但是相反的定义提供了与量子力学中的狄拉克符号更平滑的连接,现在也偶尔被数学家使用。某些作者接受约定 < , > 在第一个分量是线性的而 < | > 在第二个分量上是线性的,尽管不普遍。
选择R 或 C作为内积空间的基域是有原因的。首先,这个域要包含一个有序关系的子域,否则就无法谈论“非负性”,因此它的特征必须是零。这样就排除了所有的有限域。基础域必须有额外的结构,比如有显著的自同构。
在某些情况下,必须考虑非负半定半双线性形式。这意味着 <x, x> 是只要求非负性,下面会展示如何处理它们。
例子
内积的一个简单的例子是实数的乘法
欧几里德空间Rn和点积构成一个内积空间:
Cn 内积的一般形式是:
M是一个任意的正定矩阵,x*是x的共轭转置。对于实数情况这对应于两个矢量的方向差异缩放的结果的点积,带有正缩放因子和正交的缩放方向。除了正交变换之外,它是加权和版本的点积,带有正的权重。
在希尔伯特空间的文章中有一些内积空间的例子,其中引出自内积的度量生成完备的度量空间。引发不完备度量空间的内积的例子出现在在区间 [a,b] 上连续复数值函数的空间 C[a, b] 上。内积是
这个空间是不完备的;比如考虑对于区间 [0,1],函数序列 { fk }k 这里的
- fk(t) 是 1 对于 t 在子区间 [0, 1/2]
- fk(t) 是 0 对于 t 在子区间 [1/2 + 1/k, 1]
- fk 仿射于 [1/2, 1/2 + 1/k]
这个序列是不收敛于一个连续函数的柯西序列。
内积空间的范数
从内积空间的内积可以很自然地定义一个范数
由内积的性质可以证明它满足作为范数的要求。这个范数就是x在内积空间中的“长度”。这个范数和内积满足:柯西-布尼亚科夫斯基-施瓦茨不等式: 对V中元素x、y,
- 证明可以在主条目上找到。
- 由柯西不等式可以看出内积的几何解释:我们可以定义两个不为零的矢量的夹角为
- 其中夹角在区间(−π, +π]上。这与常见的欧几里德空间的情况相似。接下来我们可以定义正交:两个不为零的矢量正交当且仅当他们的内积为零(夹角为 π / 2)。
- 我们可以看到||·||的定义使得 V成为一个 赋范矢量空间 ,因此也是一个








 内积空间在数学中是具有内积结构的矢量空间,它允许我们讨论矢量的长度、夹角和正交性。内积空间的概念来源于欧几里得空间,是泛函分析的基础。此外,文章还介绍了内积空间的定义、性质、应用,以及与点积、叉积的关系,展示了在物理学和计算机图形学中的应用。
内积空间在数学中是具有内积结构的矢量空间,它允许我们讨论矢量的长度、夹角和正交性。内积空间的概念来源于欧几里得空间,是泛函分析的基础。此外,文章还介绍了内积空间的定义、性质、应用,以及与点积、叉积的关系,展示了在物理学和计算机图形学中的应用。



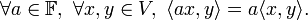




 是
是


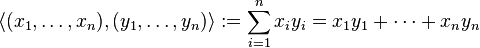



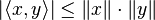

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 614
614

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








