推荐系统学习之概率算法及其增量算法

0.絮

1. 前些阵子了参加了一个天池的推荐比赛，做了一些，想了很多，因此有了下文。顺便了解过一点markdown，发现还挺好的。这次用用看。
2. 不久之前在使用链表的时候，遇到一个困难：怎么让有序链表的有序产生应有的提升查询效率的作用。答案：skip_link

1.推荐算法与概率

谈到推荐吧，我知道的也很少，总括的这种就不吹了。第一个和概率有关的推荐算法应该是“关联规则挖掘”，就是置信度、支持度那个，我就不多言了，接下来一个的则是“Page Rank”，这一个方法曾经被广泛的用于搜索引擎的网页排名中，亦是本文将要关注的重点对象。而选择这一个too young too naive的算法出发的原因就是it is simple。

2.环境设定

在PR(PageRank)中，只有一个要素：网页，一种关系：网页与网页之间的Arrow(矢量：既有大小又有方向)，而在推荐中涉及两个要素：U 用户和I 物品，一种关系：用户作用（购买、浏览、评价）了物品的Arrow。为了能够尽情的抄袭 PR我们做以下两点假设：
- U和I的地位是等价，我们可以尽情的把它们当做Page来处理。
- 每一个Array（作用）都是双向的 。
完全不了解PR的朋友可以点击脑补一下

2.1.转移矩阵 T

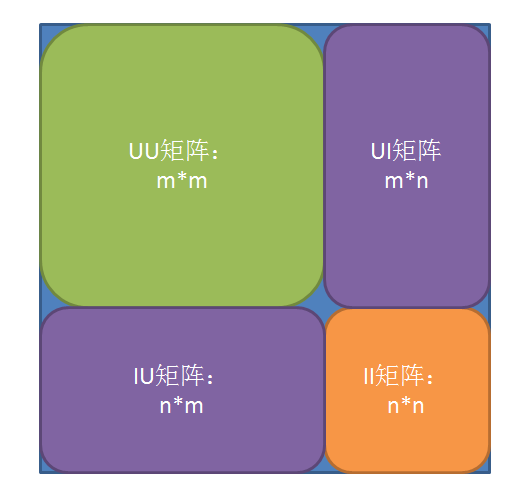
与PR类似，转移矩阵T是这个方法中的关键部分。转移矩阵如下图所示：分为四部分。

• UU矩阵：用户到用户之间的转移矩阵，为0矩阵，m为用户个数。
• UI矩阵 ：用户到物品的转移矩阵，用户购买的物品取值为1/NumI(NumI为用户购买物品数量)。
• IU矩阵 ：物品到用户的转移矩阵，购买过该物品的用户位置取值1/NumU(NumU为该物品的购买用户数)。
• II矩阵 ：商品到商品的转移矩阵，为0矩阵，n为物品个数。
  整体是一个（m+n）的方阵，前面m个是用户的部分，后面n个为商品的部分。

2.2得分矩阵 S

与T矩阵类似也分为4个部分：

• UU矩阵：向用户到用户的推荐得分。
• UI矩阵 ：向用户推荐物品的得分矩阵。
• IU矩阵 ：向物品推荐用户的得分矩阵。
• II矩阵 ：向商品推荐商品的得分矩阵。
• 整体是一个（m+n）的方阵，初始得分记做S₀，为单位矩阵。

始终满足以下等式：

1. $S_{n+1} = S_nT$
2. $S_n=S_0 T^n$

不难发现

1. 当n为偶数时，S_n中的紫色块为0矩阵，可以解释为同类元素之间的相似性（包括物品相似性和用户相似性）。
2. 当n为奇数时，S_n中的非紫色块为0矩阵，可以解释为不同类元素之间的相似性（向用户推荐物品得分以及向物品推荐用户得分）。

3.该方法的简单性质

3.1Sn 可计算

$S_n=S_0 T^n$敬爱的数学老师曾经告诉我们一个技巧：$T=PAP^{-1}$而这一过程称为矩阵对角化，如果使用矩阵求逆的方法来求A、P矩阵，其算法复杂度主要取决与这个求逆运算，而矩阵求逆运算的复杂度为