!!!Chapter 9 Graph Algorithm (9.1 ~ 9.3) Topological Sort/Shortest-Path

9.1 Definition

Basic Component:

A graph G = (V, E) consists of a set of vertices(顶点), V, and a set of edges, E. Each edgeis a pair (v, w), where v,w ∈ V。 Edges are sometimes referred to as arcs.

If the pair is ordered, then the graph is directed. Directed graphs are sometimes referred to as digraphs.

Vertex w is adjacent to v if and only if (v, w) ∈ E.

Sometimes an edge has a third component, known as either a weight or a cost.

Path:

A path in a graph is a sequence of vertices w1, w2, w3, ..., wN such that (wi, w(i+1)) ∈ E for 1≤ i ＜ N. Thelength of such a path is the number of edges on the path, which is equal to N-1

We allow a path from a vertex to itself; if this path contains no edges, then the path length is 0. If the graph contains an edge (v, v) from a vertex to itself, then the path v is referred to as a loop.

A simple path is a path such that all vertices are distinct, except that the first and last could be the same.

A cycle in a directed graph is a path of length at least 1 such that w1 = wN; this cycle is simple if the path is simple. For undirected graph, we required the edges to be distinct.

A directed graph is acyclic if it has no cycles. A directed acyclic graph is sometimes referred to by its abbreviation,DAG.

Connected:

An undirected graph is connected if there is a path from every vertex to every other vertex. A directed graph with this property is called strongly connected.

If the directed graph is not strongly connected, but the underlying graph is connected, then the graph is said to be weakly connected.

A complete graph is a graph in which there is an edge between every pair of vertices.

9.1.1 Representation of Graphs

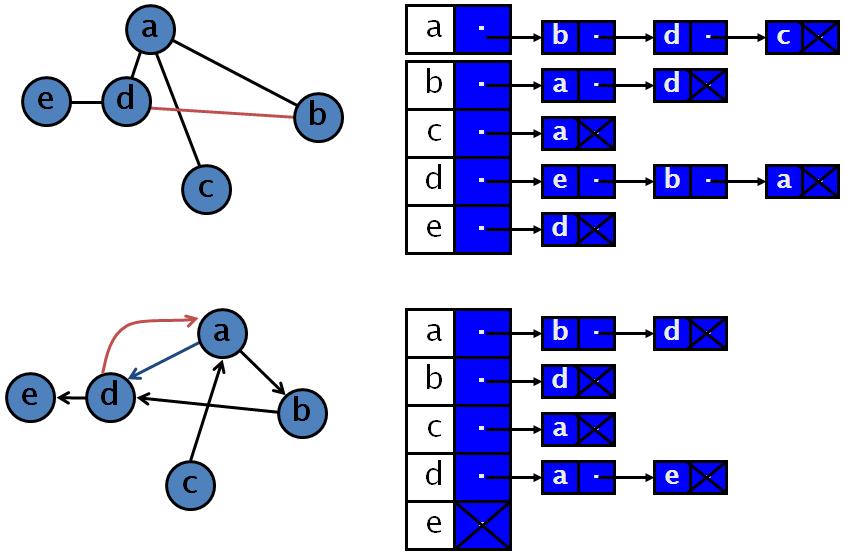
One simple way to represent a graph is to use a two-dimentional array. This is known as anadjacency matrix representation.

For each edge(u, v), we set A[u][v]=1; otherwise the entry in the array is 0. If the edge has a weight associated with it, then we can set A[u][v] equal to the weight and use either a very large or a very small weight as a sentinel to indicate nonexistent edges.

This implementation has the merit of extreme simplicity, the space requirement isΘ（|V|^2）. An adjacency matrix is an appropriate representation if the graph is dense:

|E| = Θ（|V|^2）

If the graph is not dense, in other words, if the graph is sparse, a better solution is an adjacency list representation. For each vertex, we keep a list of all adjacent vertices. The space requirement is then O(|E|+|V|).

Adjacency lists are the standard way to represent graphs. Undirected graphs can be similarly represented; each edge (u, v) appears in two lists, so the space usage essentially doubles.

If the vertices have names, we must provide a mapping of names to numbers. The easiest way to do this is to use a hash table, in which we store a name and  an internal number ranging from 1 to |V| for each vertex.

Adjacency List:

9.2 Topological Sort

A topological sort is an ordering of vertices in a directed acyclic graph, such that if there is a path from vi to vj, then vj appears after vi in the ordering.

It is clear that a topological ordering is not possible if the graph has a cycle.

The ordering is not necessarily unique; any legal ordering will do.

Simple algorithm to find a topological ordering:

1. find any vertex with no incoming edges. (If every vertex has incoming edge, then there must be a cycle)

2. Print this vertex and remove it, along with its edges.

3. Apply the same strategy to the rest of the graph.

To formalize the algorithm, we define the indegree of a vertex v as the number of edges (u, v).

Simple topological sort pseudocode:

void Topsort( Graph G )
{
    int Counter;
    Vertex V, W;

    for( Counter = 0; Counter < NumVertex; Counter++ )
    {      
// return the vertex with degree 0, and has no Counter value
        V = FindNewVertexOfDegreeZero(); 
        if( V == NotAVertex )
        {
            Error( "Graph has a cycle" );
            break;
        }
        TopNum[V] = Counter; // use Counter value to decide order
        for each W adjacent to V
            Indegree[W]--;
    }
}

Since there are |V| calls, and each call takes O(|V|) time, the time complexity isO(|V|^2)

Improved Algorithm

We can improve the performance of the algorithm by keeping all the vertices o indegree0 in a special box. TheFindNewVertexOfIndegreeZerothen returns any vertex in the box. When we decrement the indegrees of the adjacent vertices, we check each vertex and place it in the box if its indegree fails to 0.

1.The indegree is computed for every vertex.

2.All vertices of indegree 0 are placed on an initially empty queue.

3.While the queue is not empty, a vertex v is removed, and all edges adjacent to v have their indegrees decremented.

4.A vertex is put on the queue as soon as its indegree fails to 0.

5.The topological ordering then is the order in which the vertices dequeue.

Pseudocodeto perform topological sort:

void Topsort( Graph G );
{
    Queue Q;
    int Counter = 0;
    Vertex V, W;
    
    Q = CreateQueue( NumVertex ); MakeEmpty( Q );
    for each vertex V
        if( Indegree[V] == 0 )
            enqueue( V, Q );

    while( !IsEmpty(Q) )
    {
        V = Dequeue(Q);
        TopNum[V] = ++Counter;    //assign next number
//for循环每次执行都减少一条边，最多执行|E|次        
        for each W adjacent to V
            if( --Indegree[W]==0 )
                Enqueue(W, Q);
    }
    if( Counter != NumVertex )
        Error("Graph has a cycle");
    DisposeQueue(Q) // Free memory
}

The time to perform this algorithm is O(|E|+|v|)

9.3 Shortest-Path Algorithm

Weighted Graph:associated with each edge (vi, vj) is a cost c(i, j) to traverse the arc.

The cost of a path v1v2...vN is c(1, 2) + c(2, 3) + ... + c(N-1, N), this is referred to as theweighted path length.

The unweighted path length is merely the number of edges: N-1.

Single-SourceShortest-path problem:

Given as input a weighted graph, G = (V, E), and a distinguished vertex, s, find the shortest weighted path from s to every other vertex in G.

Generally,when it is not specified whether we are referring to a weighted or an unweighted path, the path is weighted if the graph is.

The loop v5, v4, v2 is known as a negative-cost cycle; when one is present in the graph, the shortest paths are not defined.

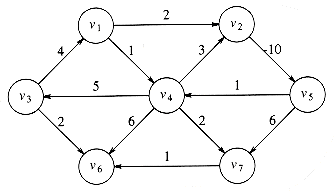
For convenience, in the absence of a negative-cost cycle, the shortest path from s to s is zero.

Currently,there are no algorithms in which finding the path from s to one vertex is any faster (by more than a constant factor) than finding the path from s to all vertices.

9.3.1Unweighted Shortest Paths

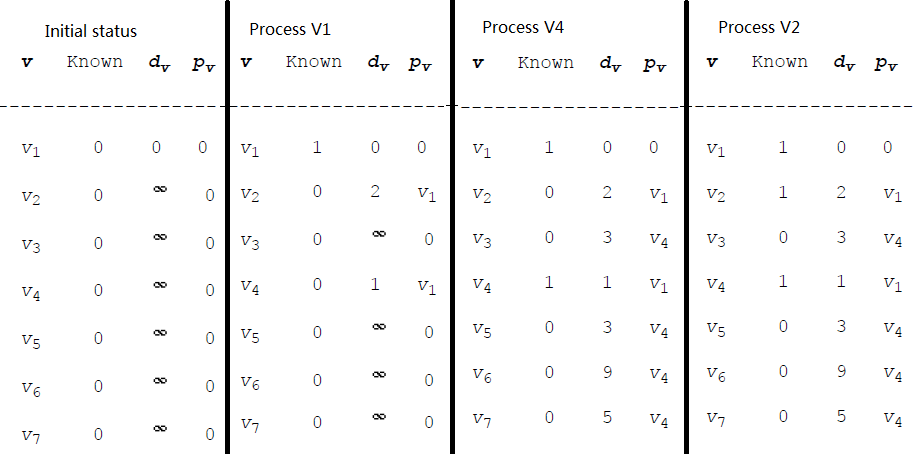
The strategy for unweighted shortest path problem is breadth-first search. It operates by processing vertices in layers: the vertices closest to the start are evaluated first, and the most distant vertices are evaluated last.

Simple Algorithm

We will use a table to keep track of each vertex:

v	Known	dv	pv
v1	0	∞	0
v2	0	0	0
...	0	∞	0

dv means the distance from s to v.

pv is the bookkeeping variable, which will allow us to print the actual path. It only remember one vertex before the final destination!

Known is set to 1 after a vertex is processed.

Pseudocode for unweighted shortest-path algorithm:

void Unweighted( Table T )
{
    int CurrDist;      //record the distance from 0 to NumVertex
    Vertex V, W;
    for( CurrDist = 0; CurrDist < NumVertex; CurrDist++ )
        for each vertex V
// if the vertex is not processed and it's distance is known from previous round
            if ( !T[V].Known && T[V].Dist==CurrDist )
            {
                T[V].Known = True;   //process this vertex
                for each W adjacent to V
                    if(T[W].Dist == Infinity)
                    {
// we set T[W].known in the next round
                        T[W].Dist == CurrDist +1;
                        T[W].Path = V;
                    }
             }
}

The running time of the algorithm is O(|V|^2)
Improved Algorithm

We can use a queue to get the result:

1. At the start, the queue contains only vertices of distance CurrDist. CurrDist should be 0 and the queue only contains the start vertex.

2. We add adjacent vertices of distance CurrDist+1

3. Once a vertex is processed, it can never enter the queue again. So known field is not used.

If some vertices are unreachable from the start node, they will never enter the queue and their distance should be infinite.

Pseudocode for improved algorithm

void Unweighted( Table T )
{
    Queue Q;
    Vertex V, W;
    Q = CreateQueue( NumVertex ); MakeEmpty( Q );
// enqueue the start vertex S
    Enqueue( S, Q );
    
    while( !IsEmpty(Q) )
    {
        V = Dequeue( Q );
        T[V].Known = True; // unnecessary
// for每次对应一条edge,最多执行|E|+|V|
        for each W adjacent to V
            if( T[W].Dist == Infinity )
            {
                T[W].Dist = T[V].Dist + 1;
                T[W].Path = V;
                Enqueue(W, Q);
            }
    }
    DisposeQueue( Q );
}

The time complexity is O(|E|+|V|).

9.3.2 Dijkstra's Algorithm

Dijkstra's algorithm is a typical greedy algorithm.

Simple Algorithm

1. Select a vertex V, which has the smallest dv among all the unknown vertices, and declares that the shortest path from s to V is known.

2. Go through all the unknown vertices that adjacent to V and compare the path through V and not through V, then decide if we need to update dw.

3. Since V is processed, select the next vertex V', which has the smallest dv' among all unknown vertices.

Declaration for Dijkstra's algorithm

typedef int Vertex;
struct TableEntry
{
    List     Header;    //adjacent list
    int      Known;
    DistType Dist;
    Vertex   Path;
};

// Vertices are numbered from 0
#define NotAVertex (-1)
typedef struct TableEntry Table[ NumVertex ];

Table initialization routine

void InitTable( Vertex Start, Graph G, Table T )
{
    int i;
    ReadGraph( G, T );    //Read graph somehow
    for(i=0; i<NumVertex; i++)
    {
        T[i].Known = False;
        T[i].Dist = Infinity;
        T[i].Path = NotAVertex;
    }
    T[Start].dist = 0;
} 

Pseudocode for Dijkstra's algorithm

void Dijkstra( Table T )
{
    vertex V, W;
    for(; ;)
    {
        V = smallest unknown distance vertex;
        if( V == NotAVertex )  //cannot access V from start point
            break;          
        
        T[V].Known = True;
        for each W adjacent to V
            if( !T[W].Known )
                if( T[V].Dist + Cvw < T[W].Dist)
                {  // update W
                    Decrease(T[W].Dist to T[V].Dist+Cvw);
                    T[W].Path = V;
                }
    }
}

Routine to print the actual shortest path

// Print the shortest path to V after Dijkstra has run
// Assume the path exists
void PrintPath (Vertex V, Table T)
{
    if (T[V].Path != NotAVertex )
    {
        PrintPath(T[V].Path, T);
        printf( " to");
    }
    printf("%v", V);  // &v is pseudocode
}

Time Complexity Analysis
1. If the graph is dense |E| = Θ|V^2|

O|V^2| will be spent finding the minimum over the course of the algorithm. Time to update dw is at most one update per edge for a total ofO|E|

So the overall complexity is O(|E|+|V^2|) = O|V^2|

In this case, the algorithm is simple and optimal.

2. If the graph is sparse, with |E| = Θ|V|

We should implement priority queue(heap) to reduce the running time to O(|E|log|V|): P 302

9.3.3 Graphs with Negative Edge Costs

9.3.4 Acyclic Graphs

9.3.5 All-Pairs Shortest Path