贪心算法（贪婪算法）

正所谓贪心不足蛇吞象

其大意是：从前有一个很穷的人救了一条蛇的命，蛇为了报答他的救命之恩，于是就让这个人提出要求，满足他的愿望。这个人一开始只要求简单的衣食，蛇都满足了他的愿望，后来慢慢的贪欲生起，要求做官，蛇也满足了他。一直到他做了宰相，还不满足，还要求做皇帝。蛇此时终于明了，人的贪心是永无止境的，于是一口就把这个人吞吃掉了。所以，蛇吞掉的是宰相，而不是大象

而今天我们要讲的是贪心算法：

        贪心算法（greedy algorithm ，又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择。

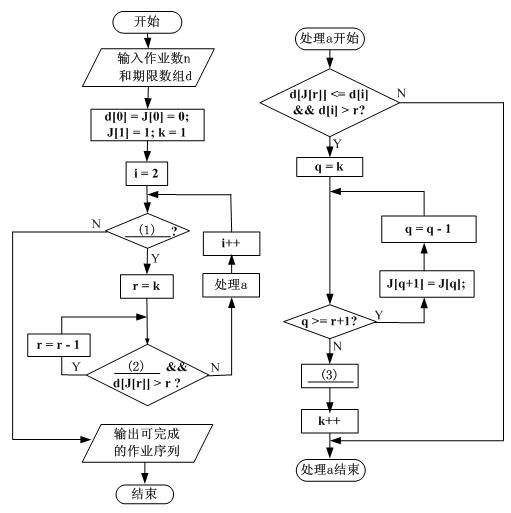
算法思路

贪心算法一般按如下步骤进行： 

①建立数学模型来描述问题 。

②把求解的问题分成若干个子问题 。

③对每个子问题求解，得到子问题的局部最优解 。

④把子问题的解局部最优解合成原来解问题的一个解  。

贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。贪心算法的特点是一步一步地进行，常以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，省去了为找最优解要穷尽所有可能而必须耗费的大量时间。贪心算法采用自顶向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择，就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪心算法不要回溯。

算法特性

贪心算法可解决的问题通常大部分都有如下的特性：

1、有一个以最优方式来解决的问题。为了构造问题的解决方案，有一个候选的对象的集合：比如不同面值的硬币 。

2、随着算法的进行，将积累起其他两个集合：一个包含已经被考虑过并被选出的候选对象，另一个包含已经被考虑过但被丢弃的候选对象  。

3、有一个函数来检查一个候选对象的集合是否提供了问题的解答。该函数不考虑此时的解决方法是否最优 [3]  。

4、还有一个函数检查是否一个候选对象的集合是可行的，即是否可能往该集合上添加更多的候选对象以获得一个解。和上一个函数一样，此时不考虑解决方法的最优性  。

5、选择函数可以指出哪一个剩余的候选对象最有希望构成问题的解 。

6、最后，目标函数给出解的值。

使用条件

利用贪心法求解的问题应具备如下2个特征 。

1、贪心选择性质

一个问题的整体最优解可通过一系列局部的最优解的选择达到，并且每次的选择可以依赖以前作出的选择，但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解 。

2、最优子结构性质

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中，至于什么问题具有什么样的贪心选择性质是不确定的，需要具体问题具体分析

解题策略

贪心算法不从整体最优上加以考虑，所做出的仅是在某种意义上的局部最优选择。使用贪心策略要注意局部最优与全局最优的关系，选择当前的局部最优并不一定能推导出问题的全局最优。贪心策略解题需要解决以下两个问题：

1、该问题是否适合使用贪心策略求解，也就是该问题是否具有贪心选择性质  ；

2、制定贪心策略，以达到问题的最优解或较优解。

要确定一个问题是否适合用贪心算法求解，必须证明每一步所作的贪心选择最终导致问题的整体最优解。证明的大致过程为：首先考察问题的一个整体最优解，并证明可修改这个最优解，使其以贪心选择开始，做了贪心选择后，原问题简化为规模更小的类似子问题。然后用数学归纳法证明通过每一步做贪心选择，最终可得到问题的整体最优解 。

存在问题

贪心算法也存在如下问题： 

1、不能保证解是最佳的。因为贪心算法总是从局部出发，并没从整体考虑 [6]  ；

2、贪心算法一般用来解决求最大或最小解 ；

3、贪心算法只能确定某些问题的可行性范围 。

应用实例

例如，平时购物找零钱时，为使找回的零钱的硬币数最少，不要求找零钱的所有方案，而是从最大面值的币种开始，按递减的顺序考虑各面额，先尽量用大面值的面额，当不足大面值时才去考虑下一个较小面值，这就是贪心算法。

有很多经典的应用，比如霍夫曼编码，普利姆和克鲁斯卡尔最小生成树算法，还有迪杰斯特拉单源最短路径算法，都是使用了这种思维。

 贪心算法的例子：

活动选择问题 ：

一、问题背景
一个调度竞争共享资源的多个活动的问题，目标是选出一个最大的互相兼容的活动集合。假定有一个n个活动的集合S={a1, a2，…，an},这些活动使用同一个资源(例如一个阶梯教室)，而这个资源在某个时刻只能供一个活动使用。
每个活动ai都有一个开始时间si和一个结束时间fi，其中0 ≤ si < fi <∞。如果被选中，任务ai发生在半开时间区间[si，fi)期间。如果两个活动ai和aj;满足[si，fi)和[sj，fj)不重叠，则称它们是兼容的。也就是说，若si≥fj或sj≥fi，则ai和aj是兼容的。
在活动选择问题中，我们希望选出一个最大兼容活动集。假定活动已按结束时间的单调递增顺序排序:

活动问题的最优子结构（可以仔细看书上原话）

这里可以通过动态规划来解决这个问题，如果用c[i,j]表示集合Sij最优解的大小，那么可以得到递归式

当然，在不知道ak的情况下，需要考查Sij中的所有活动，寻找最优解：

贪心选择
1、对于活动选择问题，什么是贪心选择？直观上，我们应该选择这样一个活动，选出它后剩下的资源应能被尽量多的其他任务所用。现在考虑可选的活动，其中必然有一个最先结束。因此，直觉告诉我们，应该选择S中最早结束的活动（它剩下的资源可供它之后尽量多的活动使用）(如果S中最早结束的活动有多个，我们可以选择其中任意一个)。
2、之后，只剩下一个子问题让我们求解：寻找在a1后开始的活动。
3、我们已经证明活动选择问题具有最优子结构性质。令kk={ai∈S: si≥fk}为在ak结束后开始的任务集合。当我们做出贪心选择，选择了a1后，剩下的S1是唯一需要求解的子问题。最优子结构性质告诉我们，如果an在最优解中，那么原问题的最优解由活动a1及子问题S中所有活动组成
4、如何确定我们直觉的正确性？

 

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> s = { 0,1,3,0,5,3,5,6,8,8,2,12 }, f = { 0,4,5,6,7,9,9,10,11,12,14,16 };
int RECURSIVE_ACTIVITY_SELECTOR(vector<int>& s, vector<int>& f, vector<int>& v_union, int k, int n)
{
	int m = k + 1;
	while (m <= n && s[m] < f[k]) {
		m++;
	}
	if (m <= n) {
		v_union.push_back(m);
		return RECURSIVE_ACTIVITY_SELECTOR(s, f, v_union,m, n);
	}
	else {
		return 0;
	}
}

int main()
{
	int n = 11;
	vector<int>v;
	RECURSIVE_ACTIVITY_SELECTOR(s, f, v,0, n);
	for (auto i : v) {
		cout << "a" << i << "  ";
	}
	return 0;
}

 钱币找零问题

有1元、5元、10元、50元、100元、500元的硬币各C1, C5, C10, C50, C100, C500枚。现在要用这些硬币来支付A元，最少需要多少枚硬币？若有解，输出最少硬币数；否则输出“-1”（0<=C1, C5, C10, C50, C100, C500<=10^9，0<=A<=10^9）

算法分析 ：贪心策略：从大到小进行币值选取

用贪心算法的思想，很显然，每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。我们可以优先使用面值大的硬币（在这里是500、100、50、10、5、1）。
————————————————

#include <cstdio>  
#include <algorithm>  
using namespace std;
int A;   
int ans=0;     //所需硬币总数  
int ret[6]={0}; //所需每种硬币的数量   
int moneycnt[6];//现有6种硬币的数量   
int moneyval[6]={1,5,10,50,100,500};//每种硬币的面值   
int main()  {  
    int i;  
    int temp;  
    scanf("%d",&A);  
    for(i=0;i<6;i++)  
     scanf("%d",moneycnt[i]);    
    for(i=5;i>=0;i--) {     //贪心策略：优先选择面值大的硬币    
    temp=min(A/moneyval[i],moneycnt[i]); //temp记录使用硬币i的枚数，注意不能超过moneycnt[i]    
       A-=(temp*moneyval[i]);    //剩余支付金额 
        ret[i]+=temp;      //使用硬币i的枚数+temp
        ans+=temp;         //已使用的硬币数+temp     
}    
    if(A>0) //A>0表示无法用现有硬币支付A元，故输出-1    
        printf("-1\n");      
    else {   //其它情况：可完成支付       
        printf("%d\n",ans);  //最少硬币数     
        for(i=0;i<6;i++)  //每种硬币需要的数量   
            printf("%d 元: %d\n",moneyval[i],ret[i]);  
    }  
    return 0;  
}  

 小船过河问题 
在漆黑的夜里，N位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话，大家是无论如何也不敢过桥去的。不幸的是，N个人一共只带了一只手电筒，而桥窄得只够让两个人同时过。如果各自单独过桥的话，N人所需要的时间已知；而如果两人同时过桥，所需要的时间就是走得比较慢的那个人单独行动时所需的时间。问题是，如何设计一个方案，让这N人尽快过桥。

输入输出
输入 
第一行是一个整数T(1<=T<=20)表示测试数据的组数 
每组测试数据的第一行是一个整数N(1<=N<=1000)表示共有N个人要过河 
每组测试数据的第二行是N个整数Si,表示此人过河所需要花时间。(0

问题分析
先将所有人过河所需的时间按照升序排序，我们考虑把单独过河所需要时间最多的两个旅行者送到对岸去，有两种方式：

1.最快的和次快的过河，然后最快的将船划回来；次慢的和最慢的过河，然后次快的将船划回来，所需时间为：t[0]+2*t[1]+t[n-1]；

2.最快的和最慢的过河，然后最快的将船划回来，最快的和次慢的过河，然后最快的将船划回来，所需时间为：2*t[0]+t[n-2]+t[n-1]。

算一下就知道，除此之外的其它情况用的时间一定更多。每次都运送耗时最长的两人而不影响其它人，问题具有贪心子结构的性质。
————————————————
 

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int t,n,pep[10001],sum;
int main()
{    
    scanf("%d",&t);
    while(t--)
    {
        memset(pep,0,sizeof(pep));
        sum = 0;
        scanf("%d",&n);
        for(int i=0;i<n;i++) scanf("%d",&pep[i]);
        sort(pep,pep+n);
        while(n > 3)
        {
            sum += min( pep[0]*2 + pep[n-1] + pep[n-2] , pep[n-1] + pep[1]*2 + pep[0] );
//          cout<<sum<<endl;
            n -= 2;
        }
        if(n == 3)
        {
            sum += pep[2] + pep[0] +pep[1];
        }
        if(n == 2)
        {
            sum +=  pep[1];
        }
        if(n == 1)
        {
            sum += pep[0];
        }
        printf("%d\n",sum);
    }
    return 0;
} 

区间覆盖问题 

数轴上有 n (1<=n<=25000)个闭区间 [ai, bi]，选择尽量少的区间覆盖一条指定线段 [1, t]（ 1<=t<=1,000,000）。

覆盖整点，即(1,2)+(3,4)可以覆盖(1,4)。

不可能办到输出-1

#include<iostream>
#include<algorithm>
#include<stdlib.h>
#include<stdio.h>
using namespace std;
/*
如果输入的区间不包括1的话，输出-1；
如果输入的区间的最大值都比t小的话，输出-1 ;
如果中间有断层的话输出-1； 
*/
struct section{
 long long int left,right;
 bool operator<(section &p){//升序比较左端点,降序比较右端点 
  return left != p.left ? left < p.left : p.right<right;
 }
};
bool cmp(section &s1,section &s2){
 return s1.right>s2.right;
}
long long int num,tag,index1,index2;//最少区间数量 
section sec[25001];
long long int t;//t就是能到达的最远的点,n是区间数
int main(){
 long long int n;long long int wid[25001][2];
 while(scanf("%ld%ld",&n,&t) != EOF){
  tag=0;num=1;index2=0;
  for(long long int i=0;i<n;i++)
   scanf("%ld%ld",&sec[i].left,&sec[i].right);
  sort(sec,sec+n,cmp);
  if(sec[0].right < t){
    cout<<-1<<endl;//不合法
    continue;
  }
  sort(sec,sec+n);
  if(sec[0].left>1){
   cout<<-1<<endl;
   continue;
  }
  if( sec[0].right >=t ){//第一条直接满足 
   cout<<1<<endl;continue;
  }
  for(long long int lop=0;lop<n;lop++){
   if(sec[tag].right+1 >= sec[lop].left){
    if( sec[lop].right >=t ){
     num++;
     cout<<num<<endl;break;
    }
   }//一组
   else{ 
    index1=sec[tag].right;
    sort(sec+tag,sec+lop,cmp);
    if(sec[tag].right+2 <= sec[lop].left){
     cout<<-1<<endl;
     break;
    }
    if(sec[tag].right>index1){//下一条新的标准线 
     num++;
     wid[index2][0]=sec[tag].left;wid[index2][1]=sec[tag].right;
     tag=lop-1;
     sec[tag].left=wid[index2][0];sec[tag].right=wid[index2][1];
     index2++;lop--;
    }
      } 
  } 
 }
 return 0;
}