今天,帕斯喵学了一下数字逻辑,发现题目完全不会做(


 )看来帕斯喵还是太笨了。
)看来帕斯喵还是太笨了。
于是呢,帕斯喵又来切题了。
Problem Description
Given a prime number
C(1≤C≤2×10![]() 5
5![]() )
)![]() , and three integers k1, b1, k2
(1≤k1,k2,b1≤10
, and three integers k1, b1, k2
(1≤k1,k2,b1≤10![]() 9
9![]() )
)![]() . Please find all pairs (a, b) which satisfied the equation
a
. Please find all pairs (a, b) which satisfied the equation
a![]() k1⋅n+b1
k1⋅n+b1![]()
![]() +
b
+
b![]() k2⋅n−k2+1
k2⋅n−k2+1![]()
![]() = 0 (mod C)(n = 1, 2, 3, ...).
= 0 (mod C)(n = 1, 2, 3, ...).
Input
There are multiple test cases (no more than 30). For each test, a single line contains four integers C, k1, b1, k2.
Output
First, please output "Case #k: ", k is the number of test case. See sample output for more detail.
Please output all pairs (a, b) in lexicographical order. (1≤a,b<C)![]() . If there is not a pair (a, b), please output -1.
. If there is not a pair (a, b), please output -1.
Please output all pairs (a, b) in lexicographical order. (1≤a,b<C)
Sample Input
23 1 1 2
Sample Output
Case #1: 1 22
Source
Recommend
这个题,窝也不好翻译啦。题目很短,大家慢慢看。
题目中给定了四个数,c,k1,b1,k2,要使得等式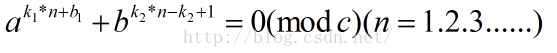
下面是证明过程:
通过(1)式和(2)式,那么呢,我们可以得到(3)式,然后我们反复的利用(3)式,就可以得到该等式恒成立啦。
剩下的就是编码了,题目说数据不超过30组,并且时间限定在5s以内,这是不是在给人提示呢。嘛,帕斯喵太笨了,只能想到用暴力。(


 )
)
刚开始萌蠢得帕斯喵用2重for循环来暴力,外层循环来遍历a的值,内层循环用来遍历b的值,结果悲剧。事实上用一个for循环来遍历a的值,通过(1)式来得到b的值,然后判断
(2)式,是否成立,这样时间复杂度就降下来了,O(n)。


代码:
#include <iostream>
#include <stdio.h>
using namespace std;
long long quickmod(long long a,long long b,long long mod)//快速幂
{
long long ans=1;
while(b)
{
if(b&1)
{
ans=ans*a%mod;
b--;
}
b=b>>1;
a=a%mod*a%mod;
}
return ans;
}
int main()
{
long long c,k1,b1,k2,res;//res用来存题目中b的值
int reg,flag=0;//flag用来记录次数
while(cin>>c>>k1>>b1>>k2)
{
reg=0;//表示没有满足题意的a,b
flag++;
printf("Case #%d:\n",flag);
for(int i=1;i<c;i++)
{
res=c-quickmod(i,k1+b1,c);
if(quickmod(i,2*k1+b1,c)==c-quickmod(res,k2+1,c))
{
cout<<i<<" "<<res<<endl;
reg=1;//表示存在满足题意的a,b;
}
}
if(reg==0)
cout<<-1<<endl;
}
return 0;
}







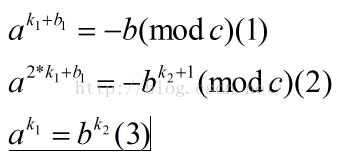














 1098
1098

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








