计算机组成原理－－最快速的除法器！

　　近来，做而论道在博客中，讨论了不少除法运算的思路，如：除法运算的位数。
　　做而论道还为几种方案设计了电路，如：八位数除以四位数、八位数除以四位数的操作、不够减的余数，真的存在吗？、减法器阵列做除法。

　　其实，讨论不同的除法方案，目的，就是想找出一个运算速度最快的除法电路。
　　在本篇博文中，做而论道将推出一个速度最快的除法运算电路。
　　前面所说的那些方案，以及《计算机组成原理》教材上给出的方案，和这次给出电路相比，都只能五体投地的甘拜下风了。
　　话不多说，直接上图。

　　在图中左上角有两组拨动开关，是用来输入被除数 X、除数 Y 的。　图中右边，用两组 LED 显示除法运算结果：商和余数。
　　由图可见，X 是 1111 1111、Y 是 1010。（为了减少篇幅，这两组数据，并没有用 LED 来显示。　但是，可以由开关所处的位置、以及观察开关旁的红蓝点，就可得到具体的数据。）
　　这两组数据，用十进制表示，就是：X = 255、Y = 10。
　　那么，X / Y 是多少呢？　心算就能得出：商 Q = 25、余数 R = 5。
　　由图中右边的 LED，可看到：Q = 0001 1001、R = 0000 0101。其十进制，正是 25 和 5。　　　
　　算的不错吧？　还可以输入其它的数据，你任意的输 ... ，本电路都能 “立即” 输出商和余数

　　如果，输入的 Y = 0000，除数为零！　就是溢出了！　这个电路，将怎么显示呢？

　　看到了吗？
　　所有的灯，都亮了！
　　特别是图中左边的【溢出标志】指示灯，它只有在发生溢出时才亮。

　　有 PROTEUS 软件的网友，可以仿照上图，画出电路。　之后，你就有一个二进制除法计算器了。　当然，你还得为两片存储器芯片，预置进去商的数据、余数的数据。　这两组数据，就难弄一些了。

　　本电路的原理，极其的简单，比《计算机组成原理》中所介绍除法电路，都简单得多！
　　哦，《计算机组成原理》中，也没介绍什么电路啊！　
　　它们，仅仅是介绍几个算法的表格，再画几个框图，就算介绍了 “组成、原理” 了。
　　这也太没有技术含量了。
　　这些框图，能否在实际中应用呢？　天（鬼）知道！

　　做而论道设计的这个除法电路，其主体，仅仅是两块 EPROM 芯片 2732。　EPROM 是指：用紫外线擦除的只读存储器。　2732 的容量仅仅是 4K * 8 位，现在来看，容量是极其的小。　这是较早期的产品，做而论道用过很多的。　现在，这类芯片早已停产了，应该买不到新品了。　当年，做而论道做过 LED 汉字显示屏，就是用这类芯片存放汉字点阵数据，即可构成一个小型的汉字库。　一片 2732，可以存放 128 个汉字（16 * 16 点）的点阵数据，或 56 个 24 * 24 点的汉字点阵数据。

　　2732 有 12 条地址线，因此，地址号码就是 12 位数。
　　那么，2732 内部就有 2^12 = 4096 = 4K 个存储单元。
　　2732 有 8 条数据线，所以，每个存储单元，就可以存放 8 位数。
　　2732 的地址号码的范围是：000H ~ FFFH。
　　2732 的单元内容可以写成：0000 0000 ~ 1111 1111B。

　　做而论道的设计思路是：把地址号码的高四位当成除数 Y、低八位当成被除数 X。
　　那么，输入一个地址号码 0FFH 时，就是相当于做除法：FF / 0。
　　这个除法是溢出的。　因此，就在两个芯片的 0FFH 单元中，都预先存进去 1111 1111。
　　以后，每当给存储器输入地址号码 0FFH，Q 和 R 两片存储器都会输出全一。
　　下图是一些地址号码及其存储单元中的预存内容。

　　把除法数据存入之后，再输入地址号码，这两片存储器就会立即输出预置的商和余数！
　　使用存储器芯片做除法器，工作速度是无与伦比的。　只需一个存储器读写周期，就能得出商和余数。　如果把这种除法器，集成在 CPU 内部，工作速度就会更快，绝对用不上一个存储器读写周期。　这就比《计算机组成原理》所介绍的那些除法方案，不知道会快上多少倍了！

　　下面再给出两张图片，都是商Ｑ存储器的预置内容。

　　上图中，左边是地址号码，红线框中的就是除数 Y，蓝线框中的是被除数 X。
　　在前 16 行，Y 都是 00H，此时的除法，就是溢出了，存储单元内容，都存入了 FFH。
　　在后 16 行，Y 都是 01H。此时，就是正常的除法了。
　　每一行有 16 个字节数据，即为 16 个存储单元的预置内容，即为 X / Y 的商值。
　　行首单元的地址，低四位是 0H，行尾单元地址的低四位是 FH。

　　2732 所能存储的内容有 4096 字节。　每行 16 字节，就是 256 行。　最后 32 行的内容如下所示。

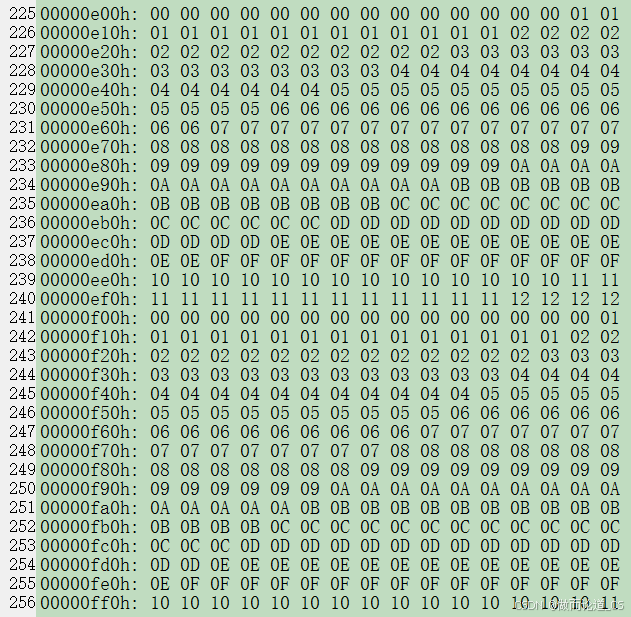
　　采用预置数来做除法，和高级语言中的设定数组变量，是异曲同工的。

　　比如，你写一个程序，其中要用到不少阶乘（n!）的值。　那么，在每次用到 2!、3! ... 8! ... 时，你当然可以调用一个函数在现场进行计算，结果也当然是可以算出来的。　但是，每次都这么算，每次都这么算，每次都这么算 ... ，你的程序，就显得太笨重了。
　　在这种前提下，就可以在程序中，设定一个数组，如：J [10]，在编程时，你就把预先算好的阶乘值，写入数组。　以后，在程序运行时，如果需要使用 2!、3! ... 8! ... 时，就可以从数组中，直接读出预置的阶乘值，即：J [2]、J [3]、J[8]。　这样做，就不用一步一步的计算了，你编写的程序，就能大大提高运行速度。

　　利用预置数的方法，在硬件中预先存好商和余数，也就不用每次都慢慢腾腾的、一位一位的移位相减移位相减移位相减的计算商和余数了。
　　学习《计算机组成原理》的同学，未必很懂硬件的设计，往往就会朦朦胧胧的感觉，书上说的挺好。　但是这些同学，应该比较熟悉软件编程的方法。　如果能想到用数组预存一些常用数据，以提高软件的运行速度，就会理解，书上所写的内容，还是有很大提升空间的。

　　把这种方法，应用在硬件中，也是早有实例的。　只不过《计算机组成原理》的作者，没有接触过这个领域。　他们也只会闷头设计除法器的方案，在算法上花费了不少心血，也确实想出了不少好法子，一一都列出在教材中。　但是，即使都学完了，也不知道究竟应该用哪一个！

　　做而论道在这里给出的电路，规模并不大，原因就是限于篇幅，有意选用了小容量的存储器芯片。　在当前，大容量的存储器芯片，型号就太多了，而且价格也不高。　用硬件来实做一个 64 位数除以 32 位的除法器，也用不了多少成本。
　　可以想见，设计 CPU 的工程师，也会想到这种方案的。　况且近年来问世的存储器，体积小容量却很大，上次买的一个小小的 TF 卡，容量竟然已经达到 128G！　因此，在 CPU 中集成这种存储电路，也就是完全可能的。　那么，我们的课本上，谆谆教导了那么多除法方案，也就没什么意思了。

－－本文完－－