数据结构学习笔记（六）优先级队列、堆和左高树

一、优先级队列

       优先级队列是0个或多个元素的集合，每一个元素都有一个优先权或值，对优先级队列执行的操作有：查找一个元素；插入一个元素；删除一个元素。在最小优先级队列中，查找和删除的元素都是优先级最小的元素；在最大优先级队列中，查找和删除的元素都是优先级最大的元素。优先级队列的元素可以有相同的优先级，对这样的元素，查找和删除可以按照任意顺序处理。优先级队列不同于一般的先进先出的队列的形式。

        以最大优先级队列为例，其C++的抽象类如下：

#pragma once
using namespace std;
//优先级队列的抽象基类
template<class T>
class maxPriorityQueue
{
public:
	virtual ~maxPriorityQueue(){}
	virtual bool empty() const = 0;//判断为空吗
	virtual int size() const = 0;//返回队列的大小
	virtual const T& top() = 0;//返回优先级最大的元素的引用
	virtual void pop() = 0;//删除队列首元素
	virtual void push(const T& theElement) = 0;//添加元素
};

二、线性表描述

        描述最大优先级队列最简单的方法是线性表。采用无序线性表描述时，插入操作很简单，但是查找和删除操作都要遍历整个线性表；采用有序线性表，查找和删除操作之间在表头或者表尾进行，但是插入操作就变得很麻烦。因此描述优先级队列最常用的是堆结构。

三、堆描述

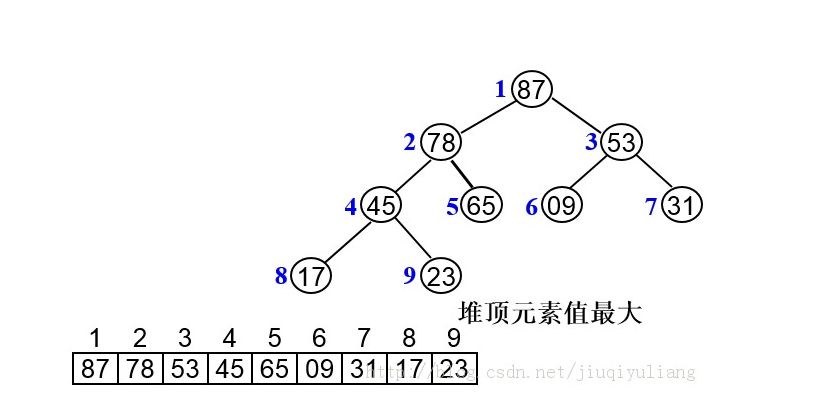
       二叉堆是一种特殊的二叉树，首先它必须是一个完全二叉树（或者近似完全二叉树），我们可以使用数组作为堆的物理存储结构；其次它满足以下性质：最大堆中双亲节点一定比左右孩纸节点要大，最小堆中双亲节点一定比左右孩子要小，并且每一个节点的左右孩纸又组成了一个最大堆（或最小堆）。

        数组下标0不存放数据，从1开始。根据完全二叉树的性质，我们可以很方便的计算双亲结点和孩纸节点的下标之间的关系。

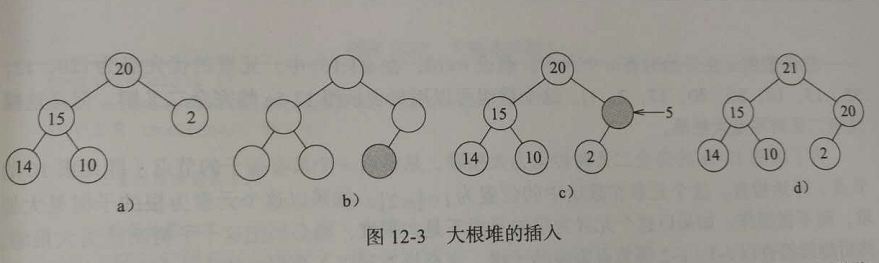
         下图中演示了最大堆的插入操作，图a是一颗5元素的大根堆。当插入一个元素后，为了维持完全二叉树的性质，其树的结构必然为图b所示。整个插入过程是这样的，把新元素插入新节点，然后沿着从新节点到根节点的路径，执行一趟起泡操作，将新元素与其父节点的元素比较交换，直到后者大于等于前者为止。如果新插入的元素是1，那么最终结果如图b；如果插入5，那么因为5大于其父节点2，执行一次起泡，最终结果如图c；如果插入21，由于其大于父节点2，执行一次起泡，而21又比父节点20大，在执行一次起泡，最终结果如图d所示：

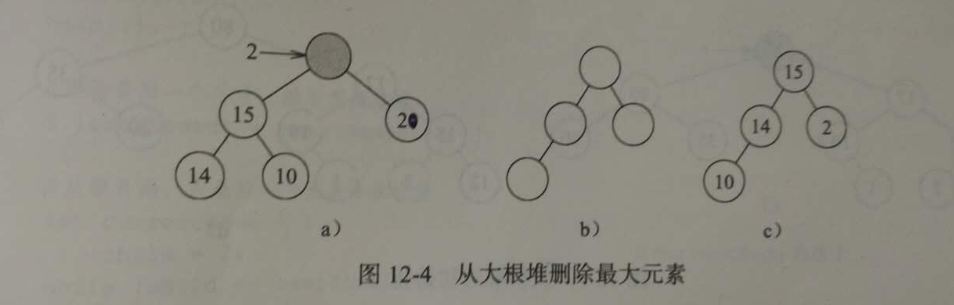
          大根堆的删除操作，就是删除根节点的元素，删除之后堆结构要重新组织以维持大根堆的性质。为此，我们把最后一个节点的元素取出，然后删除该节点维持完全二叉树的结构，此时根节点为空，但我们不能把该元素直接放入根节点，我们应该从根节点开始向下逐级寻找位置。在上图12-3（d）中，删除21以后，把最后一个节点2删除，然后寻找元素2应该插入的位置，根节点肯定不行，根的左右孩纸中20比较大，我们将20提前到根节点，然后2放在右孩纸的位置，此时是合适的，最终结果如图12-3图a所示。在下图12-4中（a）模拟了这个过程。接着我们删除根节点20，删除后的树结构如下图b，我们删除最后一个节点10，然后寻找10应该插入的位置，也是从根节点开始找，我们把15提前到根节点，发现10不适合插入左孩纸的位置，继续向下寻找，把14提前，最后结果如图c所示。

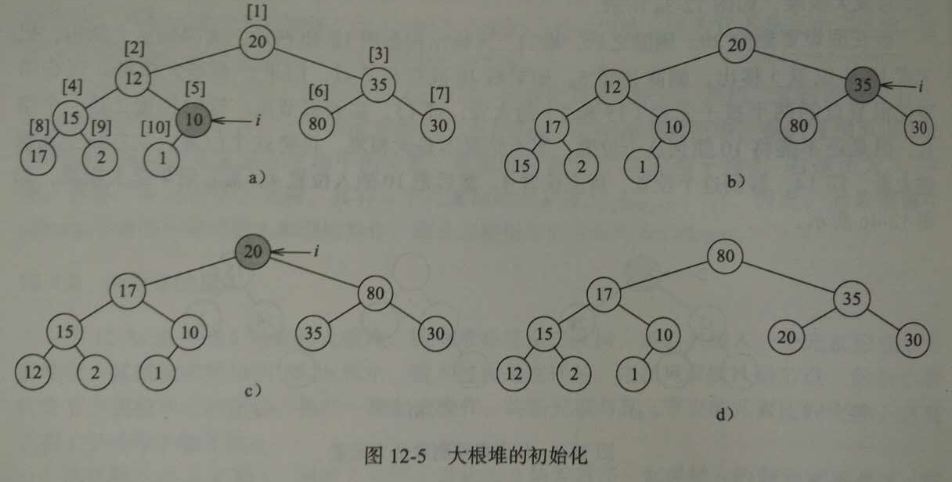
            在使用堆前，首先我们应该先建立一个堆，即堆的初始化。假设数组有n=10个元素，在数组a{1:10}中，元素的优先级为【20,12,35,15,10,80,30,17,2,1】。这个数组可以表示为下图12-5（a）的完全二叉树，接下来就要进行堆化。根据完全二叉树的性质，i=n/2是最后一个有孩纸的节点，我们从i开始往前遍历直到根节点1，对每一个节点都要堆化，以维持最大堆的性质。下图中，我们从节点5开始，符合最大堆的性质；接着看节点4，我们把17和15互换，如下图b；接着看3，以此类推。

              整个操作的C++实现如下：

#pragma once
#include<iostream>
#include <sstream>
#include <algorithm>
#include"maxPriorityQueue.h"

using namespace std;

//堆是一个完全二叉树，使用数组存储在时间空间上有好处
template<class T>
class maxHeap :public maxPriorityQueue<T>
{
public:
	//构造函数，复制构造函数和析构函数
	maxHeap(int initialCapacity = 10)
	{
		if (initialCapacity < 1)
			{ cerr << "The Capacity of Heap should be >0"; e