数据结构学习笔记（七）竞赛树

一、竞赛树

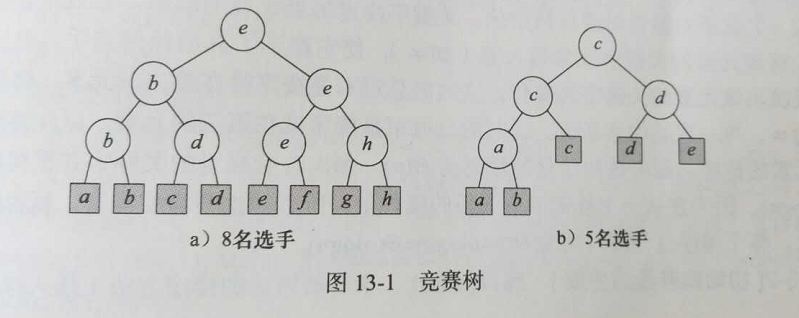
         假设有n个选手参加一场网球比赛，比赛规则是“突然死亡法”，即只要输一场就会被淘汰。一对一进行比拼，最后只剩下一个选手保持不败。下图13-1中显示了比赛过程，有a~h一共8名选手。这个比赛使用二叉树进行表示，每一个外部节点表示一名选手，每一个内部节点表示一场比赛，该节点的孩子表示比赛的选手。在同一层的内部节点代表一轮比赛，可以同时进行。在第一轮比赛中，对阵的选手有ab之间、cd之间、ef之间以及gh之间。每一场比赛的胜利者被记录在代表该比赛的内部节点中。在下图a中，第一轮比赛的胜利者为b、d、e和h，其余四位选手直接淘汰；下一轮比赛的对阵是bd之间、eh之间，胜利者是b和e，并且进入决赛；最后胜利者是e，放在根节点上。整个比赛过程见图a所示。图b中给出5名选手参加的比赛，从a到e，最后的胜利者是c。

         

       上图的两颗树都是完全二叉树。现实中竞赛所对应的树不一定是完全二叉树，但是这样做会使得比赛的场次最少。而且上面的竞赛树每一个内部节点记录的是比赛的赢者，我们称之为赢者树。如果内部节点记录的是比赛的输者，我们称之为输者树。应用中赢者树更加直观，但是输者树的实现效率更高。

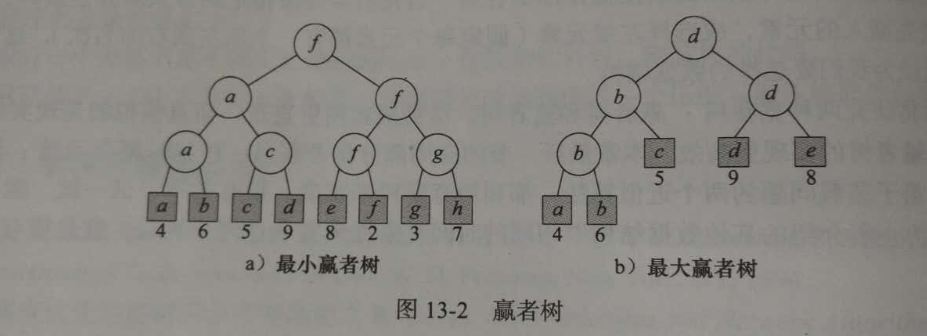
       我们定义赢者树：有n个选手的一颗赢者树是一颗完全二叉树，它有n个外部节点和n-1个内部节点，每一个内部节点记录的是在该节点进行比赛的胜利者。我们定义最小赢者树，每一场比赛分数少的选手获胜；最大赢者树中，每一场比赛分数多的选手获胜。在分数相等时，左孩纸表示的选手获胜。下图13-2中a是一颗有8名选手的最小赢者树，b是一颗有5名选手的最大赢者树。每一个外部节点下面的数字表示选手的分数。

        

二、赢者树

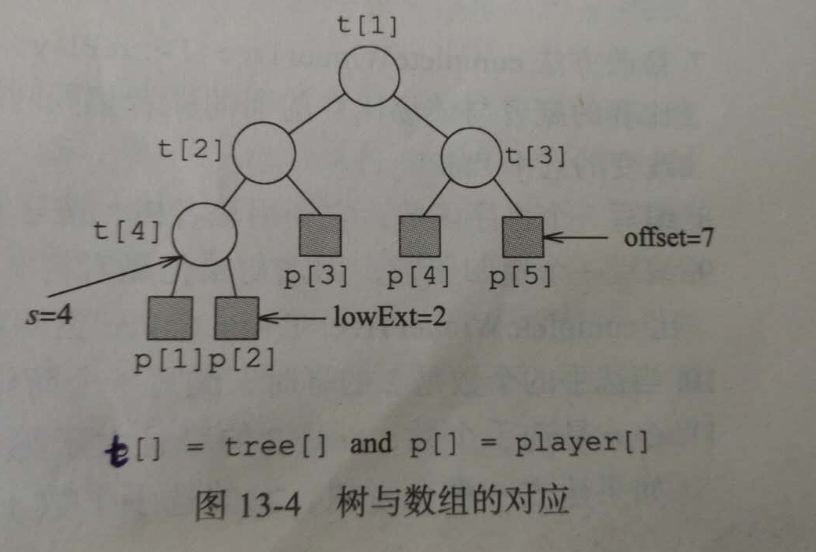
       我们使用完全二叉树的数组表示赢者树。一颗赢者树有n名选手，需要n-1个内部节点 tree[1:n-1]。选手或者外部节点用数组 player[1:n] 表示，因此 tree[i] 是数组player的一个索引，类型为int。在赢者树的节点 i 对应比赛中的赢者 tree[i] 。图13-4给出在5个选手的赢者树中，各节点与数组 tree 和 player 之间的对应关系。

       

      为实现这种对应关系，我们必须能够确定外部节点 player[i]  的父节点 tree[p]。当外部节点的个数为n时，内部节点的个数为n-1。最低层最左端的内部节点，其编号为s，并且有s=2^log（n-1）。因此，最底层内部节点的个数