计算理论课后习题整理

第一章1

1.1描述DNF的状态图

1.2 画出DFA形式化描述

 1.3 DNF由形式化描述画出状态图

1.6 （作业题）画出识别下述语言的DFA状态图 

• 每个圆圈都要有字母表的输出箭头
• 如果不符合条件的直接引向死胡同圆圈，在那个圆圈里不管输入什么还是在圆圈里
• “至少有几个”有几个就先画几个箭头，最后的圆圈为接受状态（两个圈）再去分别判断前面几个圆圈输入后是否在这几个里去判断应该引向哪
• “至多有几个”上面的反例，最后的圆圈为死胡同（死循环）
• 画出符合条件的后，对于剩余的判断加上某个输入字母表字母后会产生什么影响

下面的没有规定有多少个状态 

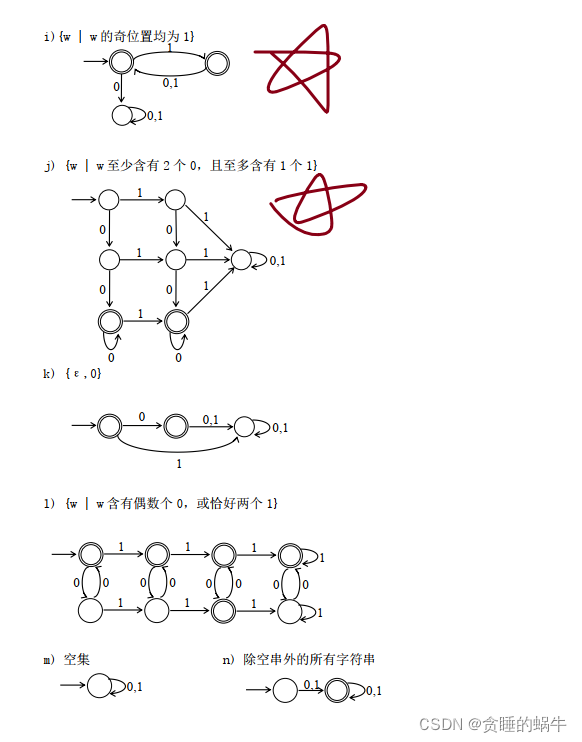
1.7（作业题） 给出识别下述语言的 NFA，且要求符合规定的状态数。

 

1.14 证明正则语言类在补运算下封闭

1.19（作业题）语言成员判别 

 

1.21 有穷自动机转换成正则表达式

 1.29 （作业题）利用泵引理证明下述语言不是正则的。

这个介绍看另一个文章 

1.24 FST有穷状态转换器介绍

1.31证明正则语言反转还是正则 

 1.32证明二进制数正则

1.37（作业题） 令Cn={x | x是一个二进制数，且是n的整数倍}。证明对于每一个n³1, Cn是正则的。

证明：下面的DFA识别Cn：(正向读)

M=( Q, {0,1} , d , q0 , F ), 其中Q＝{0,1,2,…，n-1},

d( i,1)=2i+1 mod n, d( i,0 )=( 2i mod n), i=0,1,2,…，n-1,

起始状态为0, F＝{0}.

这里i表示当前数mod n余i.

下面的DFA识别CnR：(反向读)

M=( Q, {0,1} , d , q0 , F ), 其中Q＝{(i,j)|i,j=0,1,2,…，n-1},

d((i,j),1)=( 2i mod n, (2i+j)mod n ), d((i,j),0)=( 2i mod n, j ), i,j=0,1,2,…，n-1

起始状态为(1,0), F＝{ (i,0) | i=0,1,…，n-1}.

这里(i,j)表示当前数mod n余j, 而下一位所表示单位数mod n余i(例如，若读下一位将达到k位，则下一位所表示单位数为10k-1).

1.53泵引理证明正则补充 

1.55求最小泵长度 

 第二章 上下文无关文法

2.6 设计上下文无关语言

 

说明语言是上下文无关文法如果可以构造出CFG那么就可以证明它是上下文无关文法。

2.2 a 证明上下文无关语言在交运算下不封闭

可以看理论知识里的通过泵引理证明A交B不是无关的 

2.2 b 证明上下文无关语言在补运算下不封闭

利用上下文无关语言在并运算下封闭和上下文无关语言在交运算下不封闭且上下文无关语言的补集也是CFL制造出矛盾。

（也可以像上面一个题一样证明ww形式  由于非ww形式可以CFL但是ww形式是非CFL 可以用泵引理证明在补运算不封闭 ）

2.3（作业题）

 2.4产生下述语言的上下文无关文法和 PDA（考试题）

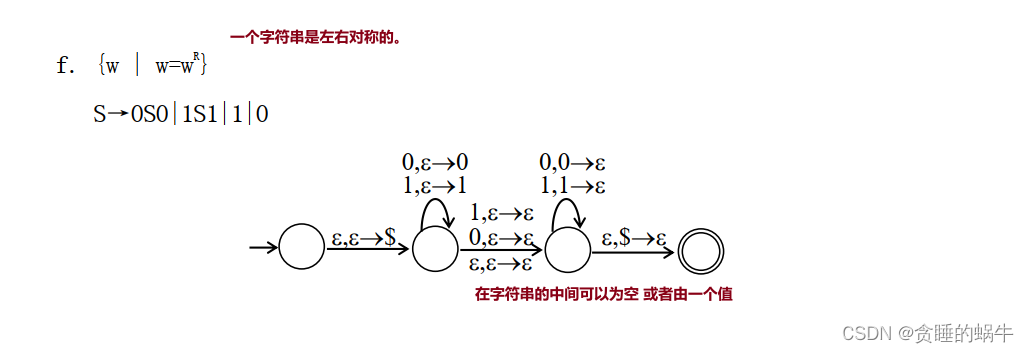
2.6 （作业题）给出产生下述语言的上下文无关文法：
 

2.7（课后题）

2.8 证明上下文无关语言类在并,连接和星号三种正则运算下封闭

 

用CFG简单点

2.10（作业题） 判断给出的文法是否是歧义的

2.11 下推自动机的非形式描述

2.10的非形式描述 

2.15 CFG 转换成等价的乔姆斯基范式文法

2.23 （作业题）

 2.30 用泵引理证明下述语言不是上下文无关的：

2.35（作业题） 

 

第三章 

3.1（作业题）输入的格局序列 

比如q1 0000 也就是q1指的右边的0

周围为  空格0000空格

1、 上面为q1指向的0，无论向左还是向右移动，指针都是指的右边的，移动的是q，并且相应的更新状态。

2、当指向没有输入时，要补上空格，比如000q0，向右移动后变为0000q空格

3、当指向没有相应的路径后，直接拒绝

3.2（作业题）

 3.4（作业题）

3.5判断

 图灵机的一个要求是一步只能做有限的工作

3.7（作业题）

 因为图灵机的一个要求是一步只能做有限的工作。
 

3.15（作业题） 证明某些可判定语言类在某些运算下封闭

3.16（作业题）图灵可识别封闭 

只需设计出图灵机来识别此种语言

第四章

4.1 图灵机当做编码（作业题）

下面具体的看课后题，背过 

2、a.判断DFA和正则表达式是否等价

          将正则表达式B转化为等价的DFA C，检测A与C是否等价，如果等价则接受，否则拒绝

     b.设ALLDFA={<A> | A是一个识别S*的DFA}。证明ALLDFA可判定 

          构造DFA B，使得L(B)= S*，检测检测<A,B>是否等价，如果等价则接受，否则拒绝

   上下文无关文法派生问题（右侧是标准答题模板）

4.3证明ALLDFA可判定（作业题）

设ALLDFA={<A> | A是一个识别S*的DFA}。

方法一：设计一个使用标记算法的TM M,（标记）

M=“对于输入<A>,其中A是一个DFA:

1. 去掉除起始状态以外的所有无用状态。标记起始状态。
2. 重复下列步骤，直到没有新的状态可被标记。
3. 对于每一个未标记状态，如果有一个到达它的转移是从某个已被标记过的状态出发的，则将其标记。
4. 如果所有的标记状态都是接受状态，则接受；否则拒绝”

方法二：构造DFA B，使得L(B)= S*。（利用EQDFA可判定）

M＝“对于输入<A>,其中A是一个DFA:

1. 检测<A,B>是否等价(EQDFA可判定)。
2. 若等价，则接受；若不等价，则拒绝。”

4.4A(CFG)判定问题

4.5 ETM的补是图灵可识别的

图灵可识别只是要能找到一个就接收，至于停机不停机不用管，下面证明它的补是图灵可识别的

4.6 对角化方法证明（作业题）

 设B是{0,1}上所有无限序列的集合，用对角化方法证明B是不可数的（不懂！！）

 

4.9 证明有回路（无限语言）（作业题）

上面第四步如果是回路的话将不会被标记

4.11和4.12 判断A接受问题（4.12作业题）

下面两个属于判断A接受问题，主要是看DFA是否接受指定的串，下面主要是构造DFA N，然后L(N)是特定的串，这个串一般是给定串的反例，然后根据这个求其交集，看是否为空

4.13判断正则表达式

正则表达式同理

 上面那个没理解

 

总结1

背过下面过程

 

 

 

 

 第五章

 5.1规约 证明EQ(CFG)是不可判定的

利用已知进行规约 

5.5证明无法映射归约

5.6 证明是传递关系 

 

 

5.28

5.34  

 

第六章

6.7 

 

 6.12

 6.15

6.23 

第七章

7.1 

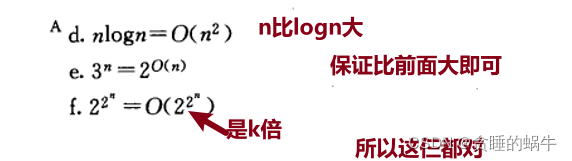
7.2 

 

7.5可满足性 

 可满足性：对变量的某个 0,1 赋值使得一个公式的值等于1

7.9

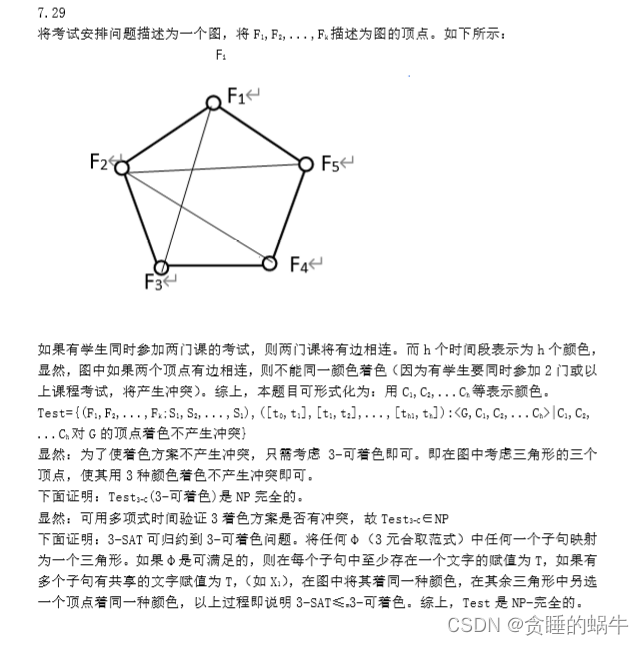
7.29

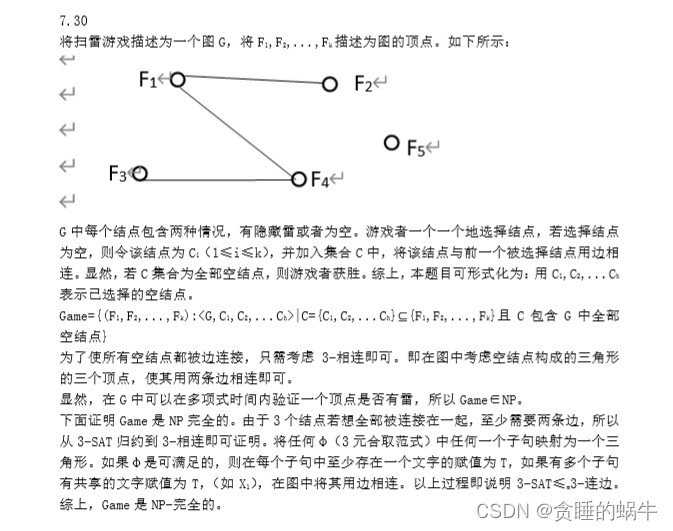
 7.30

7.36

7.39

7.40