计算理论基础作业答案（自作版）

形式语言与自动机部分

---

第一次课后作业

1. 使用归纳法证明，对字母表Σ中的任意字符串x，x的前缀有|x|+1个。

证明：

当x为空串时，|x|=0。x的前缀只有x（即空串），所以此时x的前缀有0+1个，结论成立。

假设当字符串x长度为k时，结论成立，即x的前缀有k+1个

对于一个字符串x‘，其前缀为它本身加上去除末尾字符的字符串x的前缀集合

所以x’的前缀个数=1+|x|=1+k+1=k+2，结论成立

综上：对字母表Σ中的任意字符串x，x的前缀有|x|+1个。

第二次课后作业

1. 文法G的生成式集如下，试给出句子id+id*id的两个不同的推导
$$E\to id|c|+E|-E|E+E|E-E|E\ast E|E/E|E\uparrow E|Fun(E)$$

1. $$E\to E+E\to E+E\ast E\to id+id\ast id$$

2. $$E\to E\ast E\to E\ast id\to E+E\ast id\to id+id\ast id$$

2. 设Σ={0, 1}，请给出Σ上下列语言的文法。
(1) 所有以0开头的串；
$$\begin{gathered} S\to 0|0A \\ A\to 0|1 \\ A\to 0A|1A \end{gathered}$$
(2) 所有以11开头，以11结尾的串；
$$\begin{gathered} S\to 1111|11A11 \\ A\to 0|1 \\ A\to 0A|1A \end{gathered}$$
(3) 所有最多有一对连续的0并且最多有一对连续的1的串；
$$\begin{gathered} S\to A|B|C|D \\ A\to \epsilon |A’|A^{\prime \prime } \\ {A}^{\prime }\to 0|01|01A^{\prime } \\ {A}^{\prime \prime }\to 1|10|10A^{\prime \prime } \\ B\to A{B}^{\prime }A \\ {B}^{\prime }\to 0|0B^{\prime } \\ C\to A{C}^{\prime }A \\ {C}^{\prime }\to 1|1C^{\prime } \\ D\to A{B}^{\prime }{C}^{\prime }A|A{C}^{\prime }{B}^{\prime }A \end{gathered}$$
(4) 所有长度为偶数的串。
$$S\to ϵ|00S|01S|10S|11S$$

第三次作业

1. 构造识别语言{x | x∈{0,1}+且x以0开头以1结尾}的DFA的形式描述或者画出它们的状态转移图。

2. 构造识别语言{x | x∈{0,1}*，如果x以1结尾，则它的长度为偶数；如果x以0结尾，则它的长度为奇数}的NFA。

3. 构造识别语言{x | x∈{0,1}+且x不含形如00的子串}∩ {x | x∈{0,1}+且x不含形如11的子串}的ε-NFA。

4. 写出表示语言{x | x∈{0,1}+并且x中至少含两个1}的正规/正则表达式。

$$\begin{gathered} L(M)=R_{13}^3 \\ {r}_{13}^3=r_{13}^2(r_{33}^2)\ast r_{32}^2+r_{12}^2 \\ =0\ast (1)0\ast 1(0+1)\ast (0+1)+0\ast (1)0\ast 1 \\ =0\ast 10\ast 1((0+1)\ast (0+1)+ϵ) \\ =0\ast 10\ast 1(0+1)\ast \end{gathered}$$

5. 构造正规/ 正则表达式((0+1)(0+1))*+((0+1)(0+1)(0+1))*的等价FA。
{X||x|为偶数或|x|为三的倍数}

第四次作业

1. {$0^{2n}$|n≥1}和{$0^{n^2}$ | n≥1}是字母表Σ={0, 1}上的语言，请分析哪个是RL，那个不是RL？如果不是，请证明你的结论；如果是RL，请构造出其有穷描述（FA、RG或者RE）。

{$0^{2n}$|n≥1}是RL，{$0^{n^2}$ | n≥1}不是RL

• 证明{$0^{n^2}$ | n≥1}不是RL：

  $\forall$非负整数k

  取x=$0^{k(k-1)}$,y=$0^k$,z=$\epsilon$，将y写作y=uvw(v!=$\epsilon$)，取i=2，

  $\because$ 1<=|v|<=k

  $\therefore$ $k^2$ < |xu$v^2$wz| < $k^2-k+2k$ < $(k+1{)}^2$

  故xu$v^2$wz长度位于两个相邻整数平方之间，不可能为某个整数的平方

  即{$0^{n^2}$ | n≥1}不是RL

• {$0^{2n}$|n≥1}的FA描述：

2. 用Myhill-Nerode定理证明字母表Σ={0, 1, 2}上的语言{$0^n{1}^m{2}^n$ | n, m≥1}不是RL。

证明：

令A={$0^n{1}^m{2}^n$ | n, m≥1}

即证$R_A$指数无穷

A的元素0，1，2按次序排列且0和2个数相同

对于$0^i$和 $0^j$(i!=j)，则二者属于不同的等价类中

考察01，001，0001…

依次需要加1个2，两个2，三个2…到达终结状态

因此在等价关系下，这一串字符串属于不同的等价类

则可构造$R_A$的无穷多个等价类

[1]=01所在等价类

[2]=001所在等价类

…

[n]=$0^n$1所在等价类

…

故$R_A$指数无穷，A不是RL

3. 判断命题“RL的每一个子集都是RL”，并证明你的结论。

不成立

考虑字母表Σ={0, 1}上的语言A={$0^n$|n≥1}，B={$0^{n^2}$ | n≥1}

显然B是A的子集且A为RL

但B不是RL

第五次作业

1. 请构造产生语言{$1^n{0}^{2m}{1}^n$ | n, m≥1}的CFG

CFG G的生成式可构造为：

S $\to$ 1S1|1A1

A$\to$ 00|0A0

故G=({S,A},{0,1},{S$\to$ 1S1|1A1,A$\to$ 00|0A0},S)

2. 构造一个算法，该算法可以判断任意CFG G=(V, T,P, S)，L(G)是否为空

利用引理5.1给出的算法，检验S是否能派生出终结符号串，若能，则L(G)非空；若不能，则L(G)为空

3. 构造识别语言{$1^n{0}^m$ | n≥m≥1}的PDA

令M=({$q_0$，$q_1$，$q_2$，$q_3$}，{0，1}，{Z，1}，$\delta$，$q_0$，Z，{$q_2$})

$\delta$($q_0$,1,Z)={($q_1$,1Z)}

$\delta$($q_0$,0,Z)={($q_3$,0)}

$\delta$($q_1$,1,1)={($q_1$,11)}

$\delta$($q_1$,0,1)={($q_2$,~)}

$\delta$($q_2$,0,1)={($q_2$,~)}

$\delta$($q_2$,0,Z)={($q_4$,Z)}

$\delta$($q_2$,1,Z)={($q_3$,Z)}

$\delta$($q_4$,0,Z)={($q_4$,Z)}

$\delta$($q_4$,1,Z)={($q_3$,Z)}

$\delta$($q_2$,1,1)={($q_3$,1)}

从$q_0$开始，若读到1则在栈中加入一个1，同时将状态改为$q_1$。$q_1$若遇到1则也在栈中加1，栈不变；若遇到0则将状态变为$q_2$，1出栈。$q_2$遇到0还是$q_2$，栈不变；遇到1则进入陷进状态$q_3$。$q_2$遇到0就一直消，直到到底遇到Z，变为$q_4$，其中$q_4$为终结状态。

4. 构造PDA M，使得N(M)={$1^n{0}^n$ | n≥1},{$1^n{0}^{2n}$|n≥1}（此题是当时理解错了，应该没有“，”表示连接

1. {$1^n{0}^n$ | n≥1}:

   令M=({$q_0$，$q_1$，$q_2$，$q_3$}，{0，1}，{A,B,C}，$\delta$，$q_0$，C，$\varnothing$)

   $\delta$($q_0$,1,A)={($q_1$,CA)}

   $\delta$($q_0$,1,C)={($q_1$,BC)}

   $\delta$($q_1$,1,B)={($q_1$,BB)}

   $\delta$($q_1$,0,B)={($q_2$,$ϵ$)}

   $\delta$($q_2$,0,B)={($q_2$,$ϵ$)}

   $\delta$($q_2$,1,C)={($q_3$,$ϵ$)}

2. {$1^n{0}^{2n}$|n≥1}:

   令M=({$q_0$，$q_1$，$q_2$，$q_3$}，{0，1}，{A,B,C}，$\delta$，$q_0$，C，$\varnothing$)

   $\delta$($q_0$,1,A)={($q_1$,CCA)}

   $\delta$($q_0$,1,C)={($q_1$,BBC)}

   $\delta$($q_1$,1,B)={($q_1$,BBB)}

   $\delta$($q_1$,0,B)={($q_2$,$ϵ$)}

   $\delta$($q_2$,0,B)={($q_2$,$ϵ$)}

   $\delta$($q_2$,1,C)={($q_3$,$ϵ$)}

3. N(M)={$1^n{0}^n$ | n≥1}{$1^n{0}^{2n}$|n≥1}（更正）
   PDA M=({q,p,r},{0,1},{B,A,Z},𝛿,q,Z, Ø)
   𝛿(q,1,Z)={(q,AZ)}
   𝛿(q,1,A)={(q,AA)}
   𝛿(q,0,A)={(p, 𝜀)}
   𝛿(p,0,A)={(p, 𝜀)}
   𝛿(p,1,Z)={(p,BB)}
   𝛿(p,1,B)={(p,BBB)}
   𝛿(p,0,B)={(r, 𝜀)}
   𝛿(r,0,B)={(r, 𝜀)}

第六次作业

1. 请用CFL缩胀定理证明下列语言{$0^n{1}^n{2}^n$ | n≥0}不是CFL

$\forall k⩾0$

取$z=0^k{1}^k{2}^k$，|z|=3k $⩾$ k

将z写作 $z=uvwxy$ ,这里|vx|$⩾$ 1,|vwx|$⩽$ k

考虑以下情况：

• v和x只含0或只含1或只含2：则 $u{v}^{2}w{x}^{2}y$ 中0,1,2个数不等，则其不属于原语言
• v中只包含0、x中只包含1或者v中只包含1、x中只包含2：则 $u{v}^{2}w{x}^{2}y$ 中0,1,2个数不等，则其不属于原语言
• v或x中包含两种不同的符号，则 $u{v}^{2}w{x}^{2}y$ 会出现这两种符号交替，结果不再属于原语言。如v中包含0和1，则$u{v}^{2}w{x}^{2}y$ 则会至少有两个01出现，不属于原语言

综上：原语言不是CFL

2. 请用Ogden引理证明语言{$2^m{1}^k{0}^n$ | k=max{n, m}}不是CFL

$\forall k⩾0$

取z=$2^k{1}^{2k+1}{0}^{2k+1}$ ，|z| > k，且指定k个2全是特别符号

将z写作 $z=uvwxy$ ,这里v,w,x满足定理中的条件

考虑以下情况：

• v或x中包含两种不同的符号，则 $u{v}^{2}w{x}^{2}y$ 会出现这两种符号交替，结果不再属于原语言
• v在$2^{+}$中，x在$1^{+}$中，$u{v}^{2}w{x}^{2}y$ 中2的个数最多增加k（<2k+1)，1的个数因为增加，不等于0的个数，故$u{v}^{2}w{x}^{2}y$ 不属于原语言
• v在$2^{+}$中，x为空串，$u{v}^{2k+1}w{x}^{2k+1}y$ 中2的个数超过0，1的个数不变，不等于2的个数，故不属$u{v}^{2k+1}w{x}^{2k+1}y$ 于原语言
• v和x都在$2^{\ast }$中，则$u{v}^{2k+1}w{x}^{2k+1}y$ 中2的个数超过0的个数，而1的个数不变，故$u{v}^{2k+1}w{x}^{2k+1}y$ 不属于原语言
• v在$2^{+}$中，x在0*中，$u{v}^{2}w{x}^{2}y$ 中0的个数增加（成为新的max），1的个数不变不等于max，故$u{v}^{2}w{x}^{2}y$ 不属于原语言

综上：原语言不是CFL

3. 证明语言{xyx | x, y∈{0, 1}+}不是CFL

$\forall k⩾0$

取x=$0^n{1}^n$ , y=1, 则z=$0^n{1}^{n}10^n{1}^n$ 且指定前k个0全是特别符号

将z写作 $z=uvwxy$ ,这里v,w,x满足缩胀定理中的条件

设|v|=j，|x|=k, j+k>0

考虑以下情况：

• v或x含两种符号时，$u{v}^{2}w{x}^{2}y\notin L$

• v,x均属于0*，取i=0，$u{v}^{i}w{x}^{i}y=0^{n-j-k}{1}^{n}10^n{1}^n\notin L$（同属于后面的x同理）

• v属于0*，x属于1*，取i=0，$u{v}^{i}w{x}^{i}y=0^{n-j}{1}^{n-k}10^n{1}^n\notin L$（同属于后面的x同理）

• v,x均属于1*，取i=0，$u{v}^{i}w{x}^{i}y=0^n{1}^{n-j-k}10^n{1}^n\notin L$（同属于后面的x同理）

• v属于1*，x属于0*，取i=0，j,k不同时为0，$u{v}^{i}w{x}^{i}y=0^n{1}^{n-j}10^{n-k}{1}^n\notin L$

综上：原语言不是CFL

第七次作业

1. 设计识别语言{$01^n{0}^{2m}{1}^n$ | n, m≥1}的图灵机

• 构造思路：

  先看形式是否为$01^{+}{0}^{+}{1}^{+}$的形式，不是则进入拒绝状态

  再左右横跳消去1，若发现某一边仍有剩余1，则拒绝

  再从最初的0后面开始，先消去2个0，不能则拒绝

  每次消去2个0，直至遇到右边界

  再向左走，发现形式为其余全为空白符号，左端为0，则接受；否则拒绝

• 具体构造：

  TM M共设 $q_{0-11}$ ,s,t,r共1个状态，带符号为0，1，|-，B(空白符),状态转移函数 $\delta$ 如下表：

  	|-	0	1	B
  s	(s,|-,R)	($q_0$,0,R)	(r,0,0)	——
  $q_0$	——	(r,0,0)	($q_1$,1,R)	——
  $q_1$	——	($q_2$,0,R)	($q_1$,1,R)	——
  $q_2$	——	($q_2$,0,R)	($q_3$,1,R)	——
  $q_3$	——	(r,0,0)	($q_3$,1,R)	——
  $q_4$	——	($q_9$,0,L)	($q_5$,B,L)	——
  $q_5$	——	($q_6$,0,L)	($q_5$,1,L)	——
  $q_6$	(r,|-,0)	($q_6$,0,L)	($q_7$,B,R)	($q_6$,B,L)
  $q_7$	——	($q_7$,0,R)	($q_8$,1,R)	($q_7$,B,R)
  $q_8$	——	——	($q_9$,B,R)	($q_4$,B,L)
  $q_9$	——	($q_{10}$,0,L)	——	(r,B,0)
  $q_{10}$	——	($q_9$,0,L)	——	($q_{11}$,B,L)
  $q_{11}$	——	(t,0,0)	(r,1,0)	($q_{11}$,B,L)

2. 试设计计算函数$n^2$的图灵机

在输入带上放上|-$0^n$，再将其转化为|-$0^{n}10^n$,再使用例7.8乘法图灵机即可

	|-	0	1	B	2
s	($q_0$,|-,R)	——	——	——	——
$q_0$	——	($q_0$,0,R)	——	($q_1$,1,L)	——
$q_1$	($q_2$,|-,R)	($q_1$,0,L)	——	——	——
$q_2$	——	($q_3$,2,R)	($q_5$,1,L)	——	——
$q_3$	——	($q_3$,0,R)	($q_3$,1,R)	($q_4$,0,L)	——
$q_4$	——	($q_4$,0,L)	($q_4$,1,L)	——	($q_2$,2,L)
$q_5$	(t,0,0)	——	——	——	($q_5$,0,L)

3. 试给出多栈机的形式定义

由九元组成

M=(Q, $\Sigma$ ,Γ,|-,B, $\delta$ ,s,t,r）

元组定义与TM相同

$\delta (q,X_1,X_2,\cdots ,X_n)=(p,D_1,[Y_2,D_2],\cdots ,[Y_n,D_n])$表示M 在状态q 从第i条带上读入符号$X_i$ ,将状态改为p,由于第1条带为只读带,内容保持不变,并将此带上的读头进行$D_1$的移动;在此后的第i条带上，内容变为$Y_i$，进行$D_i$的移动

第八次作业

1. 给定两个TM M, N，证明下述问题是不可判定的。
(1) 是否L(M)=L(N)；
(2) 是否L(M)∩L(N)=φ；
(3) 是否L(M)∩L(N)是一个递归集。

【证明】

(1)：令A=L(M)

构造映射

$$P(A)=\{\begin{array}{c}T,当A=L(N)\\ F,当A\ne L(N)\end{array}$$

因为L(M)和L(N)均是r.e.集，故等于L(M)的r.e.是否等于L(N)是集合r.e.类的非平凡性质

由Rice定理可得：是否L(M)=L(N)是不可判定的

(2)：令A=L(M)∩L(N)

由r.e.的交集也是r.e.可得A为r.e.

由A是否是空集是不可判定的

可得：是否L(M)∩L(N)=φ也是不可判定的

(3)：令A=L(M)∩L(N)

由r.e.的交集也是r.e.可得A为r.e.

构造映射

$$P(A)=\{\begin{array}{c}T,当A是递归集\\ F,当A不是递归集\end{array}$$

则A是否是递归集是不可判定的

故可得：是否L(M)∩L(N)是递归集也是不可判定的

【解法二】用归约（反证）来做
以(1)为例，假设取L(N)=φ,若L(M)=L(N)可判定则空集问题可判定，则矛盾，故(1)不可判定
同理，(2)、(3)可假设L(M)=L(N)，归约成空集问题和递归集问题

2. 在通用图灵机编码中，用子串111作为M的描述的“括号”，用子串11作为转移函数的各个函数编码的分割符。然而，M的编码后面的w中也同样会出现这两种子串，通用图灵机为什么不会将后面出现的11, 111与作为“括号”和分割符的111和11混淆。

因为M的编码和后面w的编码中间隔了一个特殊符号#

3. 证明对于单字母表上的PCP是可判定的。

在单字母表$\Sigma$(不妨设 Σ = { 0 } \Sigma=\{0\} Σ={0})上两个字符串的表A和B：
$A=w_{a_1},w_{a_2},\dots ,w_{a_k},(w_{a_i}=0^{a_i})$

$B=w_{b_1},w_{b_2},\dots ,w_{b_k},(w_{b_i}=0^{b_i})$。
其中，$w_i\in \Sigma$(i=1, 2, …, k)。
构造TM M，若A的字符串的长度最小值大于B的字符串的长度最大值，或A的字符串的长度最大值小于B的字符串的长度最小值，则拒绝；否则则接受。

则M可判定此PCP

4. 构造LBA M，使得L(M)={ww | w∈{0, 1}*}。

LBA M共设 $q_{0-9}$ ,s,t,r共13个状态，带符号为$0，1，0^{\prime }，0^{"}，1^{\prime }，1^{"}，|-，-|,B$(空白符),状态转移函数 $\delta$ 如下表：

	|-	0	1	B	-|	0’	0"	1’	1"
s	($q_0$,|-,R)
$q_0$		($q_1$,0’,R)	($q_1$,1’,R)				(r,0",0)		(r,1",0)
$q_1$		($q_1$,0,R)	($q_1$,1,R)		($q_2$,-|,L)		($q_2$,0",L)		($q_2$,1",L)
$q_2$		($q_3$,0",L)	($q_3$,1",L)
$q_3$		($q_3$,0,L)	($q_3$,1,L)			($q_0$,0’,R)	($q_4$,0",L)	($q_0$,1’,R)	($q_4$,1",L)
$q_4$	($q_5$,|-,R)					($q_4$,0’,L)		($q_4$,1’,L)
$q_5$				(t,B,0)		($q_6$,B,R)		($q_8$,B,R)
$q_6$						($q_6$,0’,R)	($q_7$,B,L)	($q_6$,1’,R)	(r,1",0)
$q_7$	(s,|-,0)			($q_7$,B,L)		($q_9$,0’,L)		($q_9$,1’,L)
$q_8$							(r,0",0)		($q_7$,B,L)
$q_9$				($q_5$,B,L)		($q_9$,0’,L)		($q_9$,1’,L)

5. 若一个CSL能被一个确定的LBA接受，则称之为确定的CSL，请证明确定的CSL的补集还是确定的CSL。

对于此确定的CSL，则有一个确定的LBA M接受它

则构造这样的LBA M‘ M’与M仅t与r状态对换

则这样的LBA M‘接受的正是确定的CSL的补集

故此补集也是确定的CSL

6. 证明一个给定的LBA是否对一切输入都停机是不可判定的。

LBA是特殊的TM

故对于TM的性质，LBA也满足

而对于TM而言，一个给定的TM是否对一切输入都停机是不可判定的

故一个给定的LBA是否对一切输入都停机也是不可判定的

---

算法复杂性部分

---

第九次作业

7.6 证明P在并、连接和补运算下封闭

• 对于两个P类问题，$P_1和P_2$对应的单带图灵机$TM{M}_1,M_2$在多项式时间内可判定

  构造这样的TM M’,对于$M_1和M_2$的接受状态都接受，拒绝$M_1和M_2$都拒绝的状态，其余与M相同

  则M’也在多项式时间内可判定

  M’对应的则是$P_1\cup P_2$,其在多项式时间内可判定

  $P_1\cup P_2\in P$

  所以P在并运算下封闭

• 对于两个P类问题，$P_1和P_2$对应的单带图灵机$TM{M}_1,M_2$在多项式时间内可判定

  构造这样的TM M’，对于输入w，检查所有w=$w_1{w}_2$

  • 在$w_1$上运行$M_1$,接受后在$w_2$上运行$M_2$，若都接受则M’接受

  • 若所有的w=$w_1{w}_2$ 都没有达到接受状态则拒绝

  所以P在连接运算下封闭

• 对于一个P类问题，$P_1$

  其对应的单带图灵机TM M在多项式时间内可判定

  构造这样的TM M’,他拒绝M的接受状态，接受M的拒绝状态，其余与M相同

  则M’也在多项式时间内可判定

  M’对应的则是$\overline{P_1}$,其在多项式时间内可判定

  $\overline{P_1}\in P$

  所以P在补运算下封闭

7.7 证明NP在并和连接运算下封闭

• 对于两个NP类问题，$P_1和P_2$对应的非确定型图灵机$NTM{M}_1,M_2$在多项式时间内可判定

  构造这样的NTM M’,他接受$M_1或M_2$的接受状态，拒绝$M_1和M_2$都拒绝的状态，其余与M相同

  则M’也在多项式时间内可判定

  M’对应的则是$P_1\cup P_2$,其在多项式时间内可判定

  $P_1\cup P_2\in NP$

  所以NP在并运算下封闭

• 对于两个NP类问题，$P_1和P_2$对应的非确定型图灵机$NTM{M}_1,M_2$在多项式时间内可判定

  构造这样的NTM M’, 对于输入w，检查所有w=$w_1{w}_2$

  • 在$w_1$上运行$M_1$,接受后在$w_2$上运行$M_2$，若都接受则M’接受

  • 若所有的w=$w_1{w}_2$ 都没有达到接受状态则拒绝

  $P_1{P}_2\in NP$

  所以NP在连接运算下封闭

7.9 无向图中的三角形是一个3-团。证明TRIANGLE$\in$P,其中TRIANGLE={<G>|G中包含一个三角形}

• 采取这样的判定方法：

  1. 在G的n个点中任取三个点（有C(n,3)=种可能）

  2. 判断这三个点之间是否两两有连线（判断为常数级）

  故该问题可用O($n^3$)复杂性解决，在多项式时间内可判定

  故TRIANGLE$\in$P

7.12 若图的结点重新排序后，G可以变得与H完全相同，则称G与H同构。令ISO={<G,H>|G和H同构}，证明ISO$\in$NP

• 构造这样的非确定的图灵机(NTM) M:

  1. 若G和H的顶点数不同，则拒绝

  2. 设G的顶点为$g_1,g_2...g_n$，H的顶点为：$h_1,h_2...h_n$

  3. G顶点的排列顺序给定，H顶点的排列顺序非确定

  4. for i :1-> n-1（一层循环）

     ​ for j:i+1 -> n（两层循环）

     ​ 判断$g_i{g}_j$和$h_i{h}_j$是否同时在或不在G和H中，若一个在，一个不在，则拒绝

  5. 接受

  而NTM M用O($n^2$)复杂性解决，在在多项式时间内可判定

  故ISO$\in$NP

第十次作业

7.19 用7.18的结果证明MAX-CLIQUE={<G,k>|G中最大团的大小恰好为k}是DP完全的

• MAX-CLQUE在DP中

  MAX-CLQUE的DP递归定义如下：

  a. D 1 P = { < G , K > ∣ G 是包含 k 团的无向图 } D_1P=\{<G,K>|G是包含k团的无向图\} D1​P={<G,K>∣G是包含k团的无向图}

  b. $D_2P={A|A=B $ \ $ C,B={<G,K+1>|G是包含k+1团的无向图},C=D_1P}$

  MAX-CLQUE即含k团但不含k+1团

• Z在多项式时间内可归约到MAX-CLQUE：

  很复杂，搬自习题课ppt：

  
  

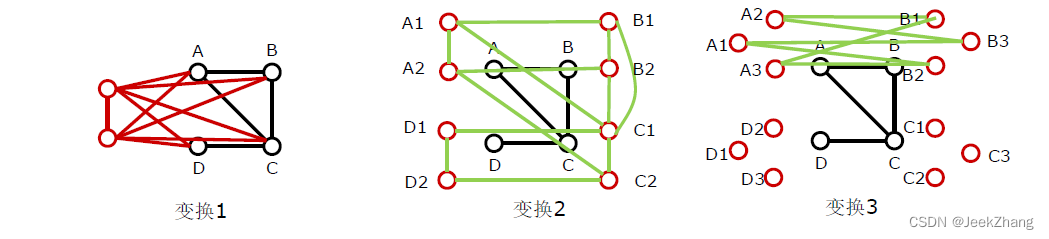
  故MAX-CLQUE是DP完全的

7.27 证明扫雷问题是NP完全的

• A={<G,<p,m>>|G是无向图，<p,m>是顶点与其标记邻雷数}

• 扫雷问题是NP问题：

  构造扫雷问题的验证机V

  V=”对输入<<G,<p,m>,T>,T为给定未知点答案（是否有雷）集合:

  1. 检查<G>的所有点四周的雷点数是否与标记数相同
  2. 若所有检查都通过，则接受；反之，则拒绝。“

  1的检查相当于遍历了所有点，每个点有4个相邻点，是与点数线性相关，是多项式时间的。

• 扫雷问题的NP完全性

7.38 证明3COLOR问题是NP完全问题

• 3COLOR问题是NP问题：

  构造3COLOR的验证机V

  V=”对输入<<G>>:

  1. 检查<G>的所有结点是否与其相邻结点颜色不一致
  2. 检查G的结点的颜色总数是否小于4
  3. 若两项检查都通过，则接受；反之，则拒绝。“

  1的检查相当于遍历了每条边的两端，是多项式时间的；2的检查可依附于1进行，故也是多项式时间的。

• 3色问题的NP完全性

7.48 证明SPATH$\in$P, LPATH是NP完全的

1. SPATH的一个多项式时间算法：广度优先

   • 将a标记为0
   • 重复下面步骤，直到标记的数>k。
   • 遍历所有标记的点p，若有q与p相连，q未被标记，则将q标记上p标记数+1

   算法的时间复杂度，每次遍历的复杂度是O(n)，遍历k次则是O(kn)<O($n^2$)，在多项式时间可完成

2. 构造LPATH的验证机V：

   V="对于输入{<<G,a,b,k>,s>}:

   • 检查s的起点是否为a，终点是否为b
   • 检查s的步数，是否大于k
   • 若两项检查都通过，则接受；反之则拒绝"

   检查1是常数级，检查2相当于遍历了s的边，故检查是多项式时间的。

   故LPATH是NP问题

   将哈密顿路径路径归约为LPATH问题：

   即求a到b中路径长度为n-2(>k)的简单路径的问题，则是LPATH的子问题

   则LPATH是NP完全的

   
   

第十一次作业

8.6 证明PSPACE难的语言也是NP难的

证明：

由NP$\subseteq$PSPACE可得：任一NP语言都是PSPACE语言

由PSPACE难的定义，任一PSPACE语言多项式时间可归约到PSPACE难的语言

故任一NP语言多项式时间可归约到PSPACE难的语言，这便是NP难的定义

故PSPACE难的语言也是NP难的

8.11 证明ADD$\in$L， PALADD$\in$L

a

证明：构造如下双带图灵机TM，一条只读输入带，一条工作带：

P=“对于输入<x,y,z>：

1. 三条指针分别指到x，y，z的末端

2. 将x指针与y指针所指的数相加，得到两位，将低位与z指针所指数对比，不同则拒绝

3. 将高位保留，待下次与x指针与y指针所指的数一起相加，并进行2的后续步骤

4. 当x，y其中一个指针到头，需要加这个数时加0即可

5. 当z到头时，x，y其中一个指针未到头，则拒绝

6. 当x，y都到头时，z未到头时，z与留下的高位对比，不一样则拒绝；若之后z还未到头，则拒绝

7. 若以上都做完，则接受“

工作带需要的空间包括三个指针的编号与其指的数，和两位结果，显然是O(logn)空间的

故ADD$\in$L

b

证明：构造如下三带图灵机TM，一条只读输入带，一条工作带，一条只写输出带：

P=“对于输入<x,y>：

1. 两条指针分别指到x，y的末端

2. 将x指针与y指针所指的数相加，得到两位，将低位写到输出带上

3. 将高位保留，待下次与x指针与y指针所指的数一起相加，并进行2的后续步骤

4. 一直到其中一个指针到头，需要加这个数时加0即可

5. 两个指针到头时，用新的两指针分别指向输出带的两端

6. 依次对比两指针所指数是否相同，不同则拒绝

7. 直至两指针相邻或重合，则接受

工作带需要的空间包括四个指针的编号与其指的数，和前面计算两位结果，显然是O(logn)空间的

8.12 证明UCYCLE$\in$L

证明：构造如下双带图灵机TM，一条只读输入带，一条工作带：

P=“对于输入<x#y>(x是点，y是边)：

1. 两条指针分别指到x，y的开端
2. 从x的点开始，到y中按顺序寻找与x相连的边
3. 记录此时的点和边
4. 将指针x移向边中的另一点，到y中从头寻找与该点相连的边
5. 循环4直到x指针回到记录的点，若是从记录的边回来的，到y中按顺序寻找该边的下一边，重复3、4、5；若不是从记录的边回来的，则接受
6. 当y中按顺序寻找不到下一边时，将x指针移到记录的x的下一位置，将x替换为该点，到y中按顺序寻找与x相连的边，重复4、5、6
7. 若以上都做完，则接拒绝

工作带需要的空间包括两个指针的编号与其指的点和边，显然是O(logn)空间的

故UCYCLE$\in$L

8.16 证明STRONGLY-CONNECTED是NL完全的

• NL：

  非确定地选取G中的两点s,t，非确定地猜测s到t和t到s的每一步。

  机器在工作带上只记录每一步当前结点的位置，而不是整两条路径。

  机器从当前结点所指向的结点中非确定地选择下一个结点。

  反复这一操作，直至s到t和t到s都完成，则接受；或者执行m步以后拒绝（m为顶点数的两倍）

  因此，STRONGLY-CONNECTED$\in$NL

• NL完全问题对数时间可归约：

  利用PATH问题中的G构造这样的G‘，将原有边全改为两条对向的有向边（(a,b)改为a→b和b→a）

  取PATH问题中两点s，t，添加这样的边：s指向除s，t的边，除s，t指向t的边

  若G’是强连通的，则G中有一条s到t的路径

  G‘中，s指向除s，t的边，除s，t指向t的边，只有当有一条有向路t→…→s时，G’是强连通的，而这一条有向路并不依赖于加边，而是依赖于原有边，即s和t有一条路径

  再来看归约所用的空间：改边和加边时，每次只处理当前边，只需要当前边的编号，显然是O(logn)空间的

• 综上：STRONGLY-CONNECTED是NL完全的

  
  

2021~2022学年第二学期期末计算理论基础考试试卷

1、下述语言哪个是正规集，哪个不是正规集？如果是，请写出其正规表达式，并构造接受该语言的有穷自动机；如果不是，请证明相应结论。（20 分）
(1) {b⁷ᵏ | k≥1}；
(2) {bᵏz | k≥1，z∈{b, c}*且包含至多 k 个字符}。

2、下述语言哪个是上下文无关语言，哪个不是上下文无关语言？如果是，请写出产生语言的格雷巴赫范式形式上下文无关文法，并将文法变换为等价的 PDA，给出 PDA
设计思想描述与具体实现；如果不是，请证明相应结论。（20 分）
(1) {u#v | u, v∈{a, b}*，且 u≠v}；
(2) {aᵏbᵏaᵏbᵏ | k≥0}。

3、试判断{<Ma, Mb> | Ma 与 Mb 是图灵机且 L(Ma)∩L(Mb)=Φ}可判定还是不可判定，并证明相应结论。（10 分）

4、给定字母表 Σ={a, b}，L={x | x 所包含的 a 的个数不是 b 的个数的两倍}，请给出判定该语言的图灵机设计思想描述与具体实现。（10 分）

5、令子集划分问题 Subset-Partition={<S, SS> | S 是一个有穷集，SS={SS1, …, SSm}是由 S 的某些子集组成的集合，m>0，使得 S
的元素可被染为黄色或绿色，且对所有 SSi，SSi 中的元素不会被染成同一种颜色}。证明 Subset-Partition 问题具有 NP 完全性，为 NP 完全问题。（10 分）

6、给定图 G=(V, E)与正整数 m，若存在 V 中 m 个顶点使得 E 中每一条边至少包含 m 个顶点中的一个顶点，则称该图有 m 顶点覆盖。顶点覆盖问题即判定对于每个输入(G, m)，G 是否有 m 顶点覆盖。若存在 V 中 m 个顶点使得其中每一对顶点在G 中都是相邻接的，则称图G 有m 团。团问题即判定对于每个输入(G, m)， G 是否有 m 团。（20 分）
(1) 请证明顶点覆盖问题可多项式时间归约至团问题，反之亦然，即团问题也可多项式时间归约至顶点覆盖问题。
(2) 假设 P=NP，说明存在一个多项式时间算法，针对图 G 可计算 G 的 m 团，或者报告 G 没有 m 团。

7、说明下述问题 I 属于 PSPACE 类，并证明对于每一个 NP 问题 Q，存在从 Q
至 I 的多项式时间归约。（10 分）
I = {<φ, m> | φ 是有至少 m 个可满足赋值的布尔公式>}