Problem Description
求C(n,m) mod p的结果, 其中p是素数
思路: 参考博客
求逆元
a*x ≡ 1(mod p)。
因为p是素数,所以我们求逆元可以用费马小定理 和 欧拉定理
a^(p-1) ≡ 1(mod p) -> a * a^(p-2) ≡ 1(mod p)。所以a^(-1) = a^(p-2)还有一种通用的求逆元方法,适合所有情况 或者 扩展欧几里得。公式如下
现在我们来证明它,已知,证明步骤如下
Lucas定理
那么得到
这样然后分别求,采用逆元计算即可。
#include<cstdio>
using namespace std;
#define ll long long
ll p, n, m;//oj问题不定义全局就超时
ll Pow(ll a, ll n)//快速幂
{
ll sum = 1;
while(n)
{
if(n&1) sum = sum*a % p;
a = a*a % p;
n >>= 1;
}
return sum;
}
ll C(ll n, ll m)//c(n,m)
{
ll a = 1, b = 1;
if(m > n) return 0;
if(m > n/2) {
m = n-m;
}
for(ll i = 1; i <= m; i++)
{
a = a*((n+i-m)%MOD) % MOD;
b = b*(i%MOD) % MOD;
}
return (a*Pow(b, MOD-2)%MOD)%MOD;//a*b^(-1)%MOD
}
ll Lucas(ll n, ll m)//Lucas定理
{
if(!m) return 1;
return C(n%p, m%p) * Lucas(n/p, m/p) % p;
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
scanf("%lld %lld %lld", &n, &m, &p);
printf("%lld\n", Lucas(n, m));//这里不用Lucas定理也能AC
}
return 0;
}










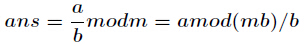
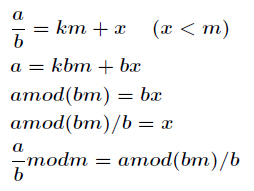
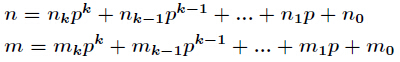
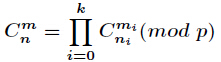














 2830
2830

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








