本博文将介绍PersonalRank算法,以及该算法在推荐系统上的应用。
将用户行为数据用二分图表示,例如用户数据是由一系列的二元组组成,其中每个元组(u,i)表示用户u对物品i产生过行为。
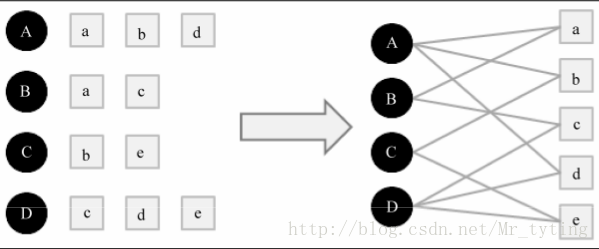
将个性化推荐放在二分图模型中,那么给用户u推荐物品任务可以转化为度量Uv和与Uv 没有边直接相连 的物品节点在图上的相关度,相关度越高的在推荐列表中越靠前。
图中顶点的相关度主要取决与以下因素:
1)两个顶点之间路径数
2)两个顶点之间路径长度
3)两个顶点之间路径经过的顶点
而相关性高的顶点一般有如下特性:
1)两个顶点有很多路径相连
2)连接两个顶点之间的路径长度比较短
3)连接两个顶点之间的路径不会经过出度较大的顶点
下面详细介绍基于随机游走的PersonalRank算法。
假设给用户u进行个性化推荐,从图中用户u对应的节点Vu开始游走,游走到一个节点时,首先按照概率alpha决定是否继续游走,还是停止这次游走并从Vu节点开始重新游走。如果决定继续游走,那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为下次经过的节点,这样经过很多次的随机游走后,每个物品节点被访问到的概率就会收敛到一个数。最终推荐列表中物品的权重就是物品节点的访问概率。
迭代公式如下:
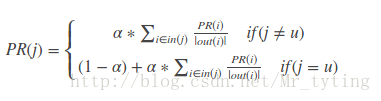
公式中PR(i)表示物品i的访问概率(也即是物品i的权重),out(i)表示物品节点i的出度。alpha决定继续访问的概率。
以下面的二分图为例,实现PersonalRank算法
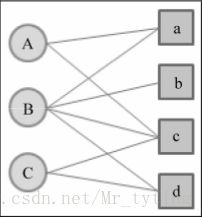
详细代码
import time
def PersonalRank(G,alpha,root,max_depth):
rank=dict()
rank={x:0 for x in G.keys()}
rank[root]=1
begin=time.time()
for k in range(max_depth):
tmp={x:0 for x in G.keys()}
for i,ri in G.items():
for j,wij in ri.items():
tmp[j]+=alpha*rank[i]/(1.0*len(ri))
tmp[root]+=(1-alpha)
rank=tmp
end=time.time()
print 'use_time',end-begin
lst=sorted(rank.items(),key=lambda x:x[1],reverse=True)
for ele in lst:
print "%s:%.3f, \t" %(ele[0],ele[1])
return rank
if __name__=='__main__':
alpha=0.8
G = {'A': {'a': 1, 'c': 1},
'B': {'a': 1, 'b': 1, 'c': 1, 'd': 1},
'C': {'c': 1, 'd': 1},
'a': {'A': 1, 'B': 1},
'b': {'B': 1},
'c': {'A': 1, 'B': 1, 'C': 1},
'd': {'B': 1, 'C': 1}}
PersonalRank(G,alpha,'b',50)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
上面算法在时间复杂度上有个明显的缺陷,每次为每个用户推荐时,都需要在整个用户物品二分图上进行迭代,直到整个图上每个节点收敛。这一过程时间复杂度非常高,不仅无法提高实时推荐,甚至离线生产推荐结果也很耗时。
比如我利用标签来设计基于图的推荐算法,数据源结构(user,item,tag),在设计用户物品标签三分图时,三分图的结构如下:
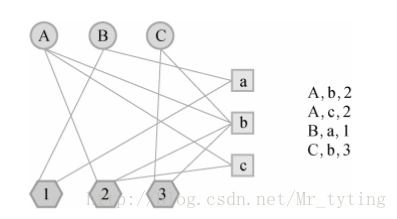
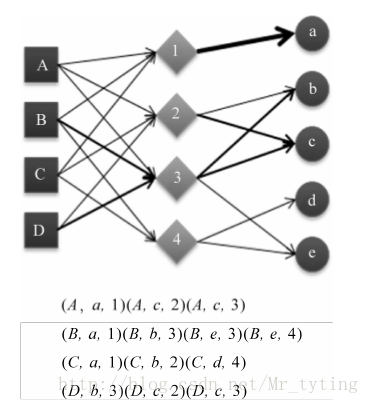
其中A,B,C是用户,a,b,c是物品,1,2,3是标签。用户和物品通过标签相连。初始是用户和物品的边的权重为1,如果用户节点和物品节点通过标签已经相连,那么边的权重就加1。而上面的二分图边权重全是1。
下面是利用标签的基于PersonalRank算法代码:
import numpy as np
import pandas as pd
import math
import time
import random
def genData():
data=pd.read_csv('test1/200509',header=None,sep='\t')
data.columns=['date','user','item','label']
data.drop('date',axis=1,inplace=True)
data=data[:5000]
print "genData successed!"
return data
def getUItem_label(data):
UI_label=dict()
for i in range(len(data)):
lst=list(data.iloc[i])
user=lst[0]
item=lst[1]
label=lst[2]
addToMat(UI_label,(user,item),label)
print "UI_label successed!"
return UI_label
def addToMat(d,x,y):
d.setdefault(x,[ ]).append(y)
def SplitData(Data,M,k,seed):
'''
划分训练集和测试集
:param data:传入的数据
:param M:测试集占比
:param k:一个任意的数字,用来随机筛选测试集和训练集
:param seed:随机数种子,在seed一样的情况下,其产生的随机数不变
:return:train:训练集 test:测试集,都是字典,key是用户id,value是电影id集合
'''
data=Data.keys()
test=[]
train=[]
random.seed(seed)
for user,item in data:
if random.randint(0,M)==k:
for label in Data[(user,item)]:
test.append((user,item,label))
else:
for label in Data[(user, item)]:
train.append((user,item,label))
print "splitData successed!"
return train,test
def getTU(user,test,N):
items=set()
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
items.add(item)
return list(items)
def new_getTU(user,test,N):
user_items=dict()
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
if (user,item) not in user_items:
user_items.setdefault((user,item),1)
else:
user_items[(user,item)]+=1
testN=sorted(user_items.items(), key=lambda x: x[1], reverse=True)[0:N]
items=[]
for i in range(len(testN)):
items.append(testN[i][0][1])
return items
def Recall(train,test,G,alpha,max_depth,N,user_items):
'''
:param train: 训练集
:param test: 测试集
:param N: TopN推荐中N数目
:param k:
:return:返回召回率
'''
hit=0
totla=0
for user,item,tag in train:
tu=getTU(user,test,N)
rank=GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
if item in tu:
hit+=1
totla+=len(tu)
print "Recall successed!",hit/(totla*1.0)
return hit/(totla*1.0)
def Precision(train,test,G,alpha,max_depth,N,user_items):
'''
:param train:
:param test:
:param N:
:param k:
:return:
'''
hit=0
total=0
for user, item, tag in train:
tu = getTU(user, test, N)
rank = GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
if item in tu:
hit += 1
total += N
print "Precision successed!",hit / (total * 1.0)
return hit / (total * 1.0)
def Coverage(train,G,alpha,max_depth,N,user_items):
'''
计算覆盖率
:param train:训练集 字典user->items
:param test: 测试机 字典 user->items
:param N: topN推荐中N
:param k:
:return:覆盖率
'''
recommend_items=set()
all_items=set()
for user, item, tag in train:
all_items.add(item)
rank=GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
recommend_items.add(item)
print "Coverage successed!",len(recommend_items)/(len(all_items)*1.0)
return len(recommend_items)/(len(all_items)*1.0)
def Popularity(train,G,alpha,max_depth,N,user_items):
'''
计算平均流行度
:param train:训练集 字典user->items
:param test: 测试机 字典 user->items
:param N: topN推荐中N
:param k:
:return:覆盖率
'''
item_popularity=dict()
for user, item, tag in train:
if item not in item_popularity:
item_popularity[item]=0
item_popularity[item]+=1
ret=0
n=0
for user, item, tag in train:
rank= GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
if item!=0 and item in item_popularity:
ret+=math.log(1+item_popularity[item])
n+=1
if n==0:return 0.0
ret/=n*1.0
print "Popularity successed!",ret
return ret
def CosineSim(item_tags,item_i,item_j):
ret=0
for b,wib in item_tags[item_i].items():
if b in item_tags[item_j]:
ret+=wib*item_tags[item_j][b]
ni=0
nj=0
for b,w in item_tags[item_i].items():
ni+=w*w
for b,w in item_tags[item_j].items():
nj+=w*w
if ret==0:
return 0
return ret/math.sqrt(ni*nj)
def Diversity(train,G,alpha,max_depth,N,user_items,item_tags):
ret=0.0
n=0
for user, item, tag in train:
rank = GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item1 in rank:
for item2 in rank:
if item1==item2:
continue
else:
ret+=CosineSim(item_tags,item1,item2)
n+=1
print "Diversity successed!",ret /(n*1.0)
return ret /(n*1.0)
def buildGrapha(record):
graph=dict()
user_tags = dict()
tag_items = dict()
user_items = dict()
item_tags = dict()
for user, item, tag in record:
if user not in graph:
graph[user]=dict()
if item not in graph[user]:
graph[user][item]=1
else:
graph[user][item]+=1
if item not in graph:
graph[item]=dict()
if user not in graph[item]:
graph[item][user]=1
else:
graph[item][user]+=1
if user not in user_items:
user_items[user]=dict()
if item not in user_items[user]:
user_items[user][item]=1
else:
user_items[user][item]+=1
if user not in user_tags:
user_tags[user]=dict()
if tag not in user_tags[user]:
user_tags[user][tag]=1
else:
user_tags[user][tag]+=1
if tag not in tag_items:
tag_items[tag]=dict()
if item not in tag_items[tag]:
tag_items[tag][item]=1
else:
tag_items[tag][item]+=1
if item not in item_tags:
item_tags[item]=dict()
if tag not in item_tags[item]:
item_tags[item][tag]=1
else:
item_tags[item][tag]+=1
return graph,user_items,user_tags,tag_items,item_tags
def GetRecommendation(G,alpha,root,max_depth,N,user_items):
rank=dict()
rank={x:0 for x in G.keys()}
rank[root]=1
for k in range(max_depth):
tmp={x:0 for x in G.keys()}
for i,ri in G.items():
for j,wij in ri.items():
tmp[j]+=alpha*rank[i]*(wij/(1.0*len(ri)))
tmp[root]+=(1-alpha)
rank=tmp
lst=sorted(rank.items(),key=lambda x:x[1],reverse=True)
items=[]
for i in range(N):
item=lst[i][0]
if '/' in item and item not in user_items[root]:
items.append(item)
return items
def evaluate(train,test,G,alpha,max_depth,N,user_items,item_tags):
recall=Recall(train,test,G,alpha,max_depth,N,user_items)
precision=Precision(train,test,G,alpha,max_depth,N,user_items)
coverage=Coverage(train,G,alpha,max_depth,N,user_items)
popularity=Popularity(train,G,alpha,max_depth,N,user_items)
diversity=Diversity(train,G,alpha,max_depth,N,user_items,item_tags)
return recall,precision,coverage,popularity,diversity
if __name__=='__main__':
data=genData()
UI_label = getUItem_label(data)
(train, test) = SplitData(UI_label, 10, 5, 10)
N=20;max_depth=50;alpha=0.8
G, user_items, user_tags, tag_items, item_tags=buildGrapha(train)
recall, precision, coverage, popularity, diversity=evaluate(train,test,G,alpha,max_depth,N,user_items,item_tags)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
实验结果:
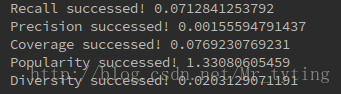
这里我只取了数据源的前5000行,因为基于逐步迭代方式的PersonalRank算法时间复杂度太高,运算太慢太耗时。如果取前10000行数据,要花一些时间才能跑出结果。
为了解决时间复杂度过高问题,我们可以从矩阵角度出发,personalrank经过多次的迭代游走,使得各节点的重要度趋于稳定,实际上我们根据状态转移矩阵,经过一次矩阵运算就可以直接得到系统的稳态。上面迭代公式的矩阵表示形式为:
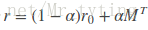 r
r
其中r是个n维向量,每个元素代表一个节点的PR重要度,r0也是个n维向量,第i个位置上是1,其余元素均为0,上面迭代公式左边有个PR(j)和PR(i),其中i是j一条入边。他们迭代最终的概率(权重)都在r中。我们就是要为第i个节点进行推荐。M是n阶转移矩阵:
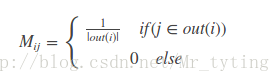
上式可以变形到:
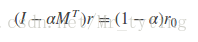
这就相当于解线性方程组了。因为M是稀疏矩阵,我们可以利用scipy.sparse中的gmres,csr_matrix解稀疏矩阵的线性方程组。还是以上面二分图为例利用PersonalRank的矩阵法求解,详细代码如下:
#coding:utf-8
import numpy as np
from numpy.linalg import solve
import time
from scipy.sparse.linalg import gmres,lgmres
from scipy.sparse import csr_matrix
if __name__=='__main__':
alpha=0.8
vertex=['A','B','C','a','b','c','d']
M=np.matrix([[0, 0, 0, 0.5, 0, 0.5, 0],
[0, 0, 0, 0.25, 0.25, 0.25, 0.25],
[0, 0, 0, 0, 0, 0.5, 0.5],
[0.5, 0.5, 0, 0, 0, 0, 0],
[0, 1.0, 0, 0, 0, 0, 0],
[0.333, 0.333, 0.333, 0, 0, 0, 0],
[0, 0.5, 0.5, 0, 0, 0, 0]])
r0=np.matrix([[0],[0],[0],[0],[1],[0],[0]])#从'b'开始游走
print r0.shape
n=M.shape[0]
#直接解线性方程法
A=np.eye(n)-alpha*M.T
b=(1-alpha)*r0
begin=time.time()
r=solve(A,b)
end=time.time()
print 'user time',end-begin
rank={}
for j in xrange(n):
rank[vertex[j]]=r[j]
li=sorted(rank.items(),key=lambda x:x[1],reverse=True)
for ele in li:
print "%s:%.3f,\t" %(ele[0],ele[1])
#采用CSR法对稀疏矩阵进行压缩存储,然后解线性方程
data=list()
row_ind=list()
col_ind=list()
for row in xrange(n):
for col in xrange(n):
if (A[row,col]!=0):
data.append(A[row,col])
row_ind.append(row)
col_ind.append(col)
AA=csr_matrix((data,(row_ind,col_ind)),shape=(n,n))
begin=time.time()
r=gmres(AA,b,tol=1e-08,maxiter=1)[0]
end=time.time()
print "user time",end-begin
rank={}
for j in xrange(n):
rank[vertex[j]]=r[j]
li=sorted(rank.items(),key=lambda x:x[1],reverse=True)
for ele in li:
print "%s:%.3f,\t" % (ele[0], ele[1])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
运行结果可知,利用稀疏矩阵的线性方程解法很快就能得出结果,不需要一步步迭代。
上面代码有个瑕疵,就是每次手动的写M矩阵,很不自动化。
下面我再在标签的推荐系统中,也即是三分图中,利用PersonalRank的矩阵解法求解r,数据源和上面的三分图一样,边的权重也是如上面三分图那样定义:详细代码如下
import numpy as np
import pandas as pd
import math
import random
from scipy.sparse.linalg import gmres,lgmres
from scipy.sparse import csr_matrix
def genData():
data=pd.read_csv('test1/200509',header=None,sep='\t')
data.columns=['date','user','item','label']
data.drop('date',axis=1,inplace=True)
data=data[:10000]
print "genData successed!"
return data
def getUItem_label(data):
UI_label=dict()
for i in range(len(data)):
lst=list(data.iloc[i])
user=lst[0]
item=lst[1]
label=lst[2]
addToMat(UI_label,(user,item),label)
print "UI_label successed!"
return UI_label
def addToMat(d,x,y):
d.setdefault(x,[ ]).append(y)
def SplitData(Data,M,k,seed):
'''
划分训练集和测试集
:param data:传入的数据
:param M:测试集占比
:param k:一个任意的数字,用来随机筛选测试集和训练集
:param seed:随机数种子,在seed一样的情况下,其产生的随机数不变
:return:train:训练集 test:测试集,都是字典,key是用户id,value是电影id集合
'''
data=Data.keys()
test=[]
train=[]
random.seed(seed)
for user,item in data:
if random.randint(0,M)==k:
for label in Data[(user,item)]:
test.append((user,item,label))
else:
for label in Data[(user, item)]:
train.append((user,item,label))
print "splitData successed!"
return train,test
def getTU(user,test,N):
items=set()
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
items.add(item)
return list(items)
def new_getTU(user,test,N):
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
if (user,item) not in user_items:
user_items.setdefault((user,item),1)
else:
user_items[(user,item)]+=1
testN=sorted(user_items.items(), key=lambda x: x[1], reverse=True)[0:N]
items=[]
for i in range(len(testN)):
items.append(testN[i][0][1])
return items
def Recall(train,test,AA,M,G,alpha,N,user_items):
'''
:param train: 训练集
:param test: 测试集
:param N: TopN推荐中N数目
:param k:
:return:返回召回率
'''
hit=0
totla=0
for user,item,tag in train:
tu=getTU(user,test,N)
rank=GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
if item in tu:
hit+=1
totla+=len(tu)
print "Recall successed!",hit/(totla*1.0)
return hit/(totla*1.0)
def Precision(train,test,AA,M,G,alpha,N,user_items):
'''
:param train:
:param test:
:param N:
:param k:
:return:
'''
hit=0
total=0
for user, item, tag in train:
tu = getTU(user, test, N)
rank =GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
if item in tu:
hit += 1
total += N
print "Precision successed!",hit / (total * 1.0)
return hit / (total * 1.0)
def Coverage(train,AA,M,G,alpha,N,user_items):
'''
计算覆盖率
:param train:训练集 字典user->items
:param test: 测试机 字典 user->items
:param N: topN推荐中N
:param k:
:return:覆盖率
'''
recommend_items=set()
all_items=set()
for user, item, tag in train:
all_items.add(item)
rank=GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
recommend_items.add(item)
print "Coverage successed!",len(recommend_items)/(len(all_items)*1.0)
return len(recommend_items)/(len(all_items)*1.0)
def Popularity(train,AA,M,G,alpha,N,user_items):
'''
计算平均流行度
:param train:训练集 字典user->items
:param test: 测试机 字典 user->items
:param N: topN推荐中N
:param k:
:return:覆盖率
'''
item_popularity=dict()
for user, item, tag in train:
if item not in item_popularity:
item_popularity[item]=0
item_popularity[item]+=1
ret=0
n=0
for user, item, tag in train:
rank= GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
if item!=0 and item in item_popularity:
ret+=math.log(1+item_popularity[item])
n+=1
if n==0:return 0.0
ret/=n*1.0
print "Popularity successed!",ret
return ret
def CosineSim(item_tags,item_i,item_j):
ret=0
for b,wib in item_tags[item_i].items():
if b in item_tags[item_j]:
ret+=wib*item_tags[item_j][b]
ni=0
nj=0
for b,w in item_tags[item_i].items():
ni+=w*w
for b,w in item_tags[item_j].items():
nj+=w*w
if ret==0:
return 0
return ret/math.sqrt(ni*nj)
def Diversity(train,AA,M,G,alpha,N,item_tags,user_items):
ret=0.0
n=0
for user, item, tag in train:
rank = GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item1 in rank:
for item2 in rank:
if item1==item2:
continue
else:
ret+=CosineSim(item_tags,item1,item2)
n+=1
print "Diversity successed!",ret /(n*1.0)
return ret /(n*1.0)
def buildGrapha(record):
graph=dict()
user_tags = dict()
tag_items = dict()
user_items = dict()
item_tags = dict()
for user, item, tag in record:
if user not in graph:
graph[user]=dict()
if item not in graph[user]:
graph[user][item]=1
else:
graph[user][item]+=1
if item not in graph:
graph[item]=dict()
if user not in graph[item]:
graph[item][user]=1
else:
graph[item][user]+=1
if user not in user_items:
user_items[user]=dict()
if item not in user_items[user]:
user_items[user][item]=1
else:
user_items[user][item]+=1
if user not in user_tags:
user_tags[user]=dict()
if tag not in user_tags[user]:
user_tags[user][tag]=1
else:
user_tags[user][tag]+=1
if tag not in tag_items:
tag_items[tag]=dict()
if item not in tag_items[tag]:
tag_items[tag][item]=1
else:
tag_items[tag][item]+=1
if item not in item_tags:
item_tags[item]=dict()
if tag not in item_tags[item]:
item_tags[item][tag]=1
else:
item_tags[item][tag]+=1
print "buildGrapha successed!"
return graph,user_items,user_tags,tag_items,item_tags
def buildMatrix_M(G):
M=[]
for key in G.keys():
lst = []
key_out = len(G[key])
for key1 in G.keys():
if key1 in G[key]:
w=G[key][key1]
lst.append(w/(1.0*key_out))
else:
lst.append(0)
M.append(lst)
print "buildMatrix_M successed!"
return np.matrix(M)
def before_GetRec(M):
n = M.shape[0]
A = np.eye(n) - alpha * M.T
data = list()
row_ind = list()
col_ind = list()
for row in xrange(n):
for col in xrange(n):
if (A[row, col] != 0):
data.append(A[row, col])
row_ind.append(row)
col_ind.append(col)
AA = csr_matrix((data, (row_ind, col_ind)), shape=(n, n))
print "before_GetRec successed!"
return AA
def GetRecommendation(AA,M,G,alpha,root,N,user_items):
items=[]
vertex=G.keys()
index=G.keys().index(root)
n = M.shape[0]
zeros=np.zeros((n,1))
zeros[index][0]=1
r0=np.matrix(zeros)
b = (1 - alpha) * r0
r = gmres(AA, b, tol=1e-08, maxiter=1)[0]
rank = {}
for j in xrange(n):
rank[vertex[j]] = r[j]
li = sorted(rank.items(), key=lambda x: x[1], reverse=True)
for i in range(N):
item=li[i][0]
if '/' in item and item not in user_items[root]:
items.append(item)
return items
def evaluate(train,test,AA,M,G,alpha,N,item_tags,user_items):
recall=Recall(train,test,AA,M,G,alpha,N,user_items)
precision=Precision(train,test,AA,M,G,alpha,N,user_items)
coverage=Coverage(train,AA,M,G,alpha,N,user_items)
popularity=Popularity(train,AA,M,G,alpha,N,user_items)
diversity=Diversity(train,AA,M,G,alpha,N,item_tags,user_items)
return recall,precision,coverage,popularity,diversity
if __name__=='__main__':
data=genData()
UI_label = getUItem_label(data)
(train, test) = SplitData(UI_label, 10, 5, 10)
N=20;max_depth=50;alpha=0.8
G, user_items, user_tags, tag_items, item_tags=buildGrapha(train)
M=buildMatrix_M(G)
AA=before_GetRec(M)
recall, precision, coverage, popularity, diversity=evaluate(train, test, AA, M, G, alpha, N, item_tags, user_items)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 333
- 334
实验结果如下:
Recall successed! 0.00734670810964
Precision successed! 0.000143424536628
Coverage successed! 0.171535580524
Popularity successed! 1.52334906099
Diversity successed! 0.0201803245387

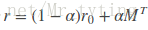









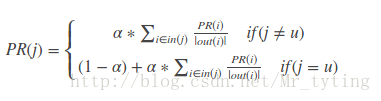



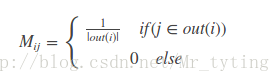
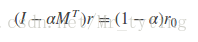
















 5693
5693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








