矩阵链乘法

用动态规划来解决矩阵链相乘的问题。

   给定由n个要相乘的矩阵构成的序列（链）<A1,A2,A3,...,An>，要计算乘积

                              A1A2A3...An

   为计算上面的乘积，可将两个矩阵相乘的标准算法作为一个子程序，根据括号给出的计算顺序做全部的矩阵乘法，一组矩阵的乘积是加全部括号的(fully parenthesized)，如果它是单个的矩阵，或是两个加全部括号的矩阵的乘积外加括号而成。矩阵的乘法满足结合率，故无论怎样加括号都会产生相同的结果。例如，如果矩阵链为<A1,A2,A3,A4>，乘积A1A2A3A4可以用五种不同方式加全部括号：

(A1(A2(A3A4))),

(A1((A2A3)A4)),

((A1A2)(A3A4)),

((A1(A2A3))A4),

(((A1A2)A3)A4).

   矩阵链加括号的顺序对求积运算的代价有很大的影响。

   动态规划的第一步是寻找最优子结构，然后利用这一子结构，就可以根据子问题的最优解构造出原问题的一个最优解。对于矩阵链乘法的问题，可以如下执行。为方便起见，几个记号如下：

   Ai...j：对乘积AiAi+1...Aj求值的结果，其中i≤j

   m[i,j]：计算矩阵Aij所需的标量乘法运算次数的最小值。

   s[i,j]：这样的一个k值，在该分裂乘积AiAi+1...Aj后可得一个最优加全部括号，也就是s[i,j]是m[i,j]最优的k值，在k出分裂最优。

   pi-1pi：pi-1表示Ai的行数，pi表示Ai的列数。其他同理。

步骤1：寻找最优子结构

假设有那么一个i≤k<j，将问题分成两部分：AiAi+1...Ak和Ak+1Ak+2...Aj，这样相乘的计算代价是最小的。

步骤2：递归

然而k具体为多少我们并不知道。

我们这样递归定义m[i,j]。

①如果i=j，则问题是平凡的，m[i,j]=m[i,i]=0

②i≠j且i<j

为计算m[i,j]，可以利用步骤1中得出的最优子结构。假设最优加全部括号将乘积AiAi+1...Aj从Ak和Ak+1分开，其中i≤k<j。因此m[i,j]就等于计算子乘积Ai...k和Ak+1...j的代价，再加上这两个矩阵相乘的代价。回忆起每个矩阵Ai是pi-1×pi的，可以看出，计算Ai...kAk+1...j要做pi-1pkpj次标量乘法，所以得到：        

m[i,j]= 

     0                         if i =j

min{m[i,k]+m[k+1,j]+pi-1pkpj   if i<j

步骤3：计算最优代价

自底向上的表格法来计算最优代价m[i,j]。

下面的伪代码假设:

1.矩阵Ai的维数是pi-1×pi，i=1,2,...,n。

2.输入一个序列p=<p0,p1,p2,...,pn>，其中length[p]=n+1。

3.此程序使用一个辅助表m[1...n][1...n]来保存m[i][j]的代价，下面简写为m[i,j]。s[1...n][1...n]来记录计算m[i,j]时取得最优代价处k的值。利用表格s来构造一个最优解。

MATRIX_CHAIN_ORDER(p)
n = length[p]-1
for i ← 1 to n
    do m[i,i] = 0
for l ← 2 to n
    do for i ← 1 to n-l+1
           do j = i+l-1
              m[i,j] = +∞
              for k ← i to j-1
                  do q = m[i,k]+m[k+1,j]+p[i-1]p[k]p[j]
                     if q < m[i,j]
                        then m[i,j] = q
                             s[i,j] = k
return m and s

结合实例来看，《算法导论》习题15.2-1:

p=<5,10,3,12,5,50,6>

n个矩阵：A5×10 A10×3 A3×12 A12×5 A5×50 A50×6

逐行解释：

1.n = length[p]-1=7-1=6

2.for(i=1;i<=n;i++)

    m[i,i]=0;

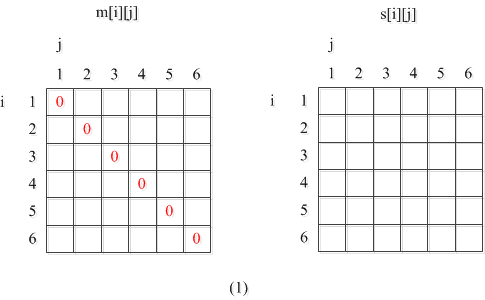
第一个for循环将平凡的情况解决，也就是i=j的情况下，对一个矩阵求乘法代价m[i,i]=0，也就是m数组的对角线为0。

有一点要注意的是：

伪代码里i,j的取值都是从1开始，是为了对应现实里A1A2...An，下面的说明也都忽略0行0列。所以我们不妨在代码里将0行0列都设为0（其他值也行），只看从1行1列开始的右上三角部分。

3.接下来的三重for循环       

for(l=2;l<=n;l++)
   for(i=1;i<=n-l+1;i++)
   {
       j = i+l-1;
       m[i][j] = 10000;
       for(k=i;k<=j-1;k++)
       {
           q = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
           if(q<m[i][j])
           {
                m[i][j] = q;
                s[i][j] = k;
            }
         }
     }

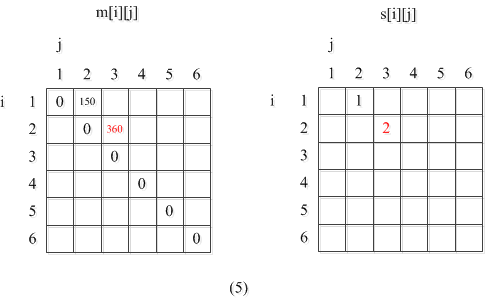
第1次循环：

l=2,i=1,j=2,这里l是矩阵链的长度，Aij的长度就是l

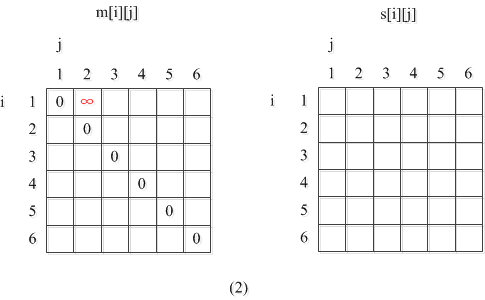
    先把m[1][2]置为一个很大的值。

    然后开始第三层循环，k:i～j-1也就是1≤k≤1，就一个值。

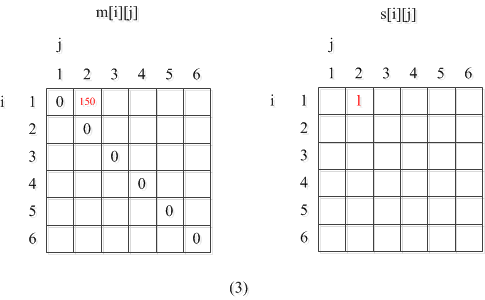
q = m[1][1]+m[2][2]+p[0]p[1]p[2]=0+0+5*10*3=150

    上面的意思是：i=1,j=2,也就是算A1A2的代价。只有两个矩阵，子结构只有一个，所以k=1。

    A12 = A11+A22+p[0]p[1]p[2],其中A11就是m[1][1]，A22就是m[2][2]。m[1][1]和m[2][2]通过查表获得。之前说的自底向上的思想，就是先计算长度l=1，也就是m[i][i]=0，填入表。然后l=2，两个子结构的长度都为1，通过查表得出m[i][j]；l=3时，那么子结构必然包含l1=1，l2=2，也可以通过查表获得；l=4，子结构组合多了，但依然可以通过查表获得。以后依次类推，只是子结构的组合更多了。

m[i][j] = q;

s[i][j] = k;

    将最优解填入表里。q是最优代价，k是最佳分裂点。

   第2次循环:

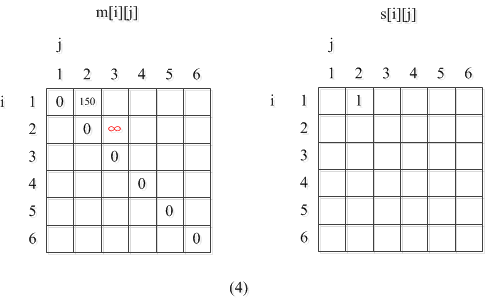
   l=2,i=2,j=3,

   m[2][3]置为很大的数：

   2≤k≤2，因为此层循环l=2，也就是两个矩阵相乘，所以k只有一个取值，别无其他的选择。在以后l=3时,k可以有2处分裂点;l=4,k有3处分裂点。

q = m[2][2]+m[3][3]+p[1]p[2]p[3]=0+0+10*3*12=360

m[2][3]=360;

s[2][3]=2;

步骤4：构造最优解

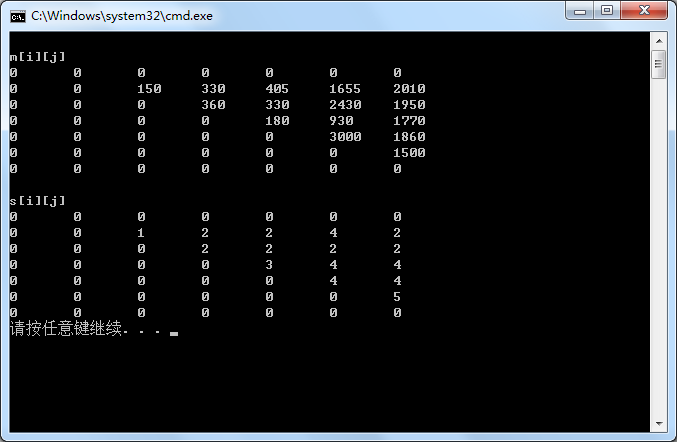
   经过多次循环，最终得的表为：

   代码运行结果：

   解释一下，如图：

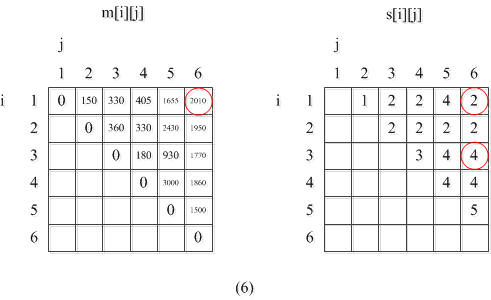
   如何看图呢？

   对表m比较直观，如本题所要求的是A1~A6的最优解，那么就看m[1][6]=2010，所以最小乘法代价是2010次。

   对于s，则告诉我们如何得到2010。同样也看s[1][6],s[1][6]=2，说明最佳分裂点在2处，即：

                     (A1A2)(A3A4A5A6)

   那么A1A2不用问，直接乘，不需要分解了。对A3A4A5A6就查s[3][6]=4,即：

                     (A3A4)(A5A6)

   总的就是：

                     (A1A2)((A3A4)(A5A6))

   我们来验证一下：

A1A2=(5×10)(10×3)=(5×3)=5×10×3=150           >m[1][2] = 150

A3A4=(3×12)(12×5)=(3×5)=3×12×5=180           >m[3][4] = 180

A5A6=(5×50)(50×6)=(5×6)=5×50×6=1500          >m[5][6] = 1500

(A3A4)(A5A6)=(3×6)=180+1500+3×5×6=1770       >m[3][6] = 1770

(A1A2)((A3A4)(A5A6))=150+1770+5×3×6=2010     >m[1][6] = 2010

   故最小代价乘积求出来，其最优加全部括号同时也给出。

#include <stdio.h>

void print(int m[7][7])
{
	int i,j;
	for(i=0;i<7;i++)
	{
		for(j=0;j<7;j++)
			printf("%d\t",m[i][j]);
		printf("\n");
	}
}

void main()
{
	int p[7]={5,10,3,12,5,50,6};
	static int m[7][7],s[7][7];
	int i,j,k,l,q,n=6;

	for(i=1;i<=n;i++)
		m[i][i] = 0;

	for(l=2;l<=n;l++)
	{
		for(i=1;i<=n-l+1;i++)
		{
			j = i + l -1;
			m[i][j] = 100000000;
			for(k=i;k<=j-1;k++)
			{
				q = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(q<m[i][j])
				{
					m[i][j] = q;
					s[i][j] = k;
				}
			}
		}
	}

	printf("\nm[i][j]\n");
	print(m);

	printf("\ns[i][j]\n");
	print(s);
}