检查一个数组是否可能是一棵二叉查询树后序遍历的结果

问题：

给一个数组，检查它是否可能是一棵二叉查询树后序遍历的结果。换句话说，是否存在一棵二叉查询树，对它进行后序遍历后，得到的数组和给定的数组完全一样。

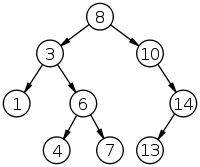
比如，对上面这个二叉查询树后序遍历后，得到的数组是：[1, 4, 7, 6, 3, 13, 14, 10, 8]。

思路：

因为二叉树后序遍历的时候，先左后右然后中间。所以，数组的最后一个一定是整个二叉查询树的根（比如 8），而且，数组前一部分比数组最后一个值（也就是二叉查询树的根）小，因为它们是根的左子树部分。数组剩余部分，是根的右子树部分。而且，在剩余部分里，所有的值都必须比根要大。这样，我们可以把原来的数组分成两个部分，然后每一个部分可以进行递归判断，直到数组的长度小于等于2。（因为当长度小于等于2时，什么样的情况都是可以的）。

我们先把给定的数组分成两个部分，即我们需要先找到数组的分界点。代码如下：

/**
 * 
 * @param array  the input array	
 * @param begin  the starting index of the array
 * @param end    the ending index of the array
 * @return   the turning point of the array, where the left part of 
 * turning point is smaller than array[end], the right 
 * part of the turning point is larger than array[end].
 */
public int turningPoint(int[] array, int begin, int end) {
	
	int tp = -1;
	for (int i = begin; i < end; i++) {
		if (array[i] > array[end]) {
			tp = i;
			break;
		}
	}
	
	return tp;
}

找到分界点后，我们还要判断从分界点开始，到数组末，是否所有的值都比数组的最后一个值（也就是根）大，否则，这样的数组不是一个二叉查询树的后序遍历。代码如下：

//check whether all the elements from strat are larger than array[end]
	public boolean checkValid(int[] array, int start, int end) {
		for (int i = start; i < end; i++) {
			if (array[i] < array[end]) return false;
		}
		return true;
	}

有了上面两个方法，我们就可以把递归写出来了，代码如下：

//the main method to check whether the array is identical to a BST's post order array
	public boolean isPostOrder(int[] array, int begin, int end) {
		// the exit
		if ((end - begin + 1) <= 2) return true;
		//get the turning point
		int turningPoint = turningPoint(array, begin, end);
		//check whether the right part of the array is valid
		boolean result = checkValid(array, turningPoint, end);  
		if (result == false) {
			return false;
		}
		// recursion
		return isPostOrder(array, begin, turningPoint - 1) && isPostOrder(array, turningPoint, end - 1);
	}

转自：http://blog.csdn.net/beiyeqingteng