Fibonacci Number （斐波那契数列）

问题：

F0 = 0
F1 = 1
Fn = Fn − 1 + Fn − 2

求Fn

Fibonacci数列是一个非常经典的用递归解决的问题。递归方法如下：

public int F(int n) {
	if (n == 0) return 0;
	else if (n == 1) return 1;
	else return F(n - 1) + F(n - 2);
}

用递归做的话，它的复杂度是指数级的，原因可以通过画递归的结构图就能马上明白了。

还有一种方法是用动态规划的实现，从第一个开始，而不是从最后一个。这样做的好处是我们不会重复计算同一个值，比如我们计算F(10)的时候，如果用递归方法，F(4)会被计算很多遍，浪费了很多时间。所以，我们可以用一个更简单的方法：

public int F(int n) {
	
	if (n == 0) return 0;
	else if (n == 1) return 1;
	else {
		int a = 0;
		int b = 1;
		for (int i = 2; i <= n; i++) {
			int c = a + b;
			a = b;
			b = c;
		}
		return b;
	}		
}

但是，这两种方法（递归和DP）都不是最好的方法，我们来看看一个更巧的方法。

首先告诉你一个事实（下图），可能你不一定会相信。如果你不相信，你可以自己动手试试看。

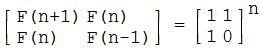
有了这个式子，问题就还没有完，我们先做一个简单的运算。

如果我们想知道2的100次方是多少，如果你稍微想一下就知道我们先找2的50次方（因为2^100 = 2^50 * 2^50），再找2的25次方，再找2的12次方，。。。，直到2的一次方。

好了，有了上面的基础，如果要算一个矩阵的n次方，我们就不会一个一个矩阵相乘了。代码如下：

public int[][] pow(int n) {
	int[][] M = {{1,1}, {1, 0}};
	if (n == 1) return M;
	else if (n%2 == 0) return multiply(pow(n/2), pow(n/2));
	else return multiply(multiply(pow(n/2), pow(n/2)), M);
}
public int[][] multiply(int[][] a, int[][] b) {
	int[][] result = new int[2][2];
	result[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
	result[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
	result[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
	result[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
	return result;
}

这样，整个算法复杂度为O(lg n) . 注意：这里的矩阵乘法并没有实现，可以写一个函数实现即可。

转载请注明出处：http://blog.csdn.net/beiyeqingteng