偶阶幻方解法 洛谷B3940[GESP样题 四级] 填幻方

相信很多dalao（看这篇文章的人）和我这个蒟蒻一样不知道c++中偶阶幻方怎么解，对吧？？？

我们先讲一下偶阶幻方：（奇数阶幻方还要我讲？？？？要讲请留言）

[GESP样题 四级] 填幻方

一、构造方法

本法构造的幻方，先根据几条通项公式，求得坐标轴上的1至n²自然数列中的部分数后，再依据本法的排列规则，可简便填充该数列其余所有的数字。

先把给定数列最小和最大的8个数，建立一个4阶幻方，作为任意n阶幻方的中心。以该4阶幻方为中心，建立两条平行的横坐标轴B、C轴，再在两条对角线位置建立两条斜坐标轴A、D轴（图一，坐标上的点，用格子代替，以便填数）

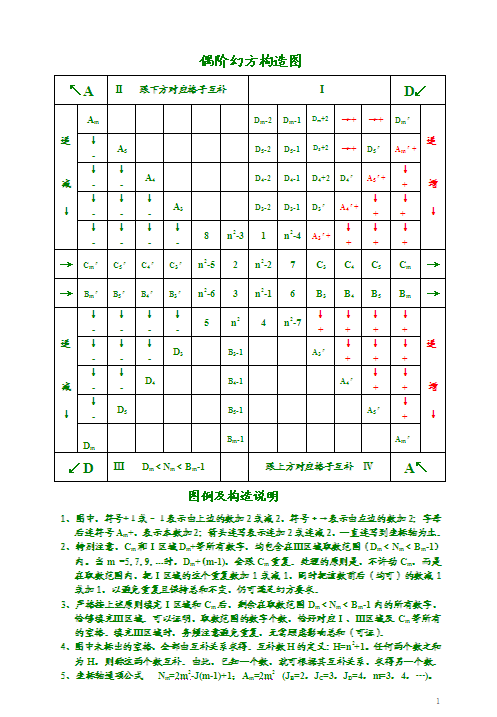
通过如下坐标轴通项公式

Nₘ=2m²-J(m-1)+1

(Jb=2，Jc=3，Jd=4，m=3，4，…)

Aₘ=2m² （ m=3，4，…)

Nₘ＇=H- Nₘ， Aₘ＇=H- Aₘ

确定各坐标轴正方向上的数字，而所有负方向上的数字，由互补的关系求得。再参照图例所示的排列规律，依次填写，即可方便得到任意偶阶幻方。

上述各式中，Nₘ表示各个坐标轴要填的数；J称初进数，对应B、C、D轴，J分别为2、3、4； m是各坐标格子序号，因为中心4阶幻方，已经占了格子序号1、2，所以m从3始取；H叫互补数，定义H=n²+1。也就是说，任何两个数之和为H，则称这两个数互补。

可以证明，由此方法得到的偶阶幻方，每一行、每一列及两条对角线上的数字之和

∑= n（1+ n²）/2

均相等，满足幻方的要求。

特别提示：

1、Ⅰ区域Dₘ+2等数字，包含在Ⅲ区域取数范围（Dₘ﹤Nₘ﹤Bₘ-1）内。当m =5,7,9,…时，这组数字中有且仅有一个数字（加m-1时），会跟C轴同序号的数字重复。处理的原则是，不许动C轴数字，在取数范围内，把本区域的这个重复数加1或减1，而把该数前后（均可）的数减1或加1，以避免重复且保持总和不变。实际上，Ⅰ区域要填的数，用Dₘ+2和（Dₘ+2）＋2，…等，只是限制了总和与个数，填什么数是不影响结果的。

2、 严格按上述原则填完Ⅰ区域后，剩余在取数范围Dₘ﹤Nₘ﹤Bₘ-1内的数字，恰能填充Ⅲ区域。可以证明，这个范围的数字个数，恰好对应所有的空格。填充Ⅲ区域时，务须注意避免重复，无需顾虑影响总和（可证）。

二、幻和的证明

本幻方的编排特点，先由通项公式求得坐标上的数字，再结合排列规律，确定一系列关键点的数字，最后利用对应格子上的数字互补的关系，求得其他空格应填的数字。

为了表述的方便，我们把所给1→n²自然数，两分其为1→n/2，(n/2)+1→n²两部分，称N≤n/2的数为小数，称N＞n/2的数为大数。由于由通项公式（Nₘ=2m²-J(m-1)+1等）决定的小数，仅是坐标序号m的函数，不含有与阶数有关的n因子，所以，小数的位置不因阶数的变化而变化；大数的数值由互补关系求得，相同的大数（Nₘ＇=H - Nₘ，H=n²+1），会随所取阶数的不同而出现在不同的位置。

特别值得注意的是，本幻方的两斜轴

（A、D），把幻方分为四个对顶的三角形区域。互为对顶的两个区域的数字，是关于中心线互补的；四条坐标轴上的数字，是关于中心点互补的；中心4阶幻方的幻和是2 H。明确这些关系，会使证明容易得多。

下面，我们就从最难下手的最下面一行开始证明。这一行得证，其余则迎刃而解。

1、 最下行的和

这一行数字的排列特点，是斜轴的左右两个数字，位在最外端。左端半行的数字，在排列时，要考虑上方和C轴的数字。咋一看，难以确定一般表式。但如果把取数范围（Dₘ﹤Nₘ﹤Bₘ-1）所包含的数全部罗列，再减去已经填掉的Ⅰ区域和C轴对应的数字，问题就给解了。

根据取数范围Dₘ﹤Nₘ﹤Bₘ-1，可以方便求得该数列所含的数字个数

（Bₘ-1）-Dₘ=

=2m²-2m+3-1-（2m²-4m+5）

=2m-3 （含Bₘ-1）

这些数中，Dₘ+2，Dₘ+4，…Dₘ+2(m-3)和Cₘ已填在Ⅰ区域和C轴，应该减掉。所以，这一行的幻和可表示为

∑₁= Dₘ+(Dₘ+1)+ (Dₘ+2)+…+

[Dₘ+(2m-3) ]-{ (Dₘ+2)+(Dₘ+4)+…+

[Dₘ+2(m-3)] }-Cₘ+H-(Dₘ-2)+

H-(Dₘ-1)+H-(Dₘ+2)+ H-(Dₘ+4)+…

+H- [Dₘ+2(m-3)]+H- Aₘ

=(2m-2)Dₘ+[1+2+…+(2m-3) ]-

(m-3) Dₘ-[2+4+…+2(m-3) ]- Cₘ+

+mH-(Dₘ-2)-(Dₘ-1)-(m-3) Dₘ-

[2+4+…+2(m-3) ] - Aₘ

而根据等差和公式，有

S₁ =1+2+…+(2m-3) = [1+(2m-3) ]

(2m-3)/2=2m²-5m+3，

S₂=2+4+…+2(m-3) =

＝2(m-3)+2 (m-3)(m-4) /2

＝2m-6+m²-7m+12

＝m²-5m+6，

∴ ∑₁=(2m-2)Dₘ+ S₁- 2(m-3) Dₘ- 2S₂-

Cₘ+mH-2Dₘ+3- Aₘ

=2mDₘ-2Dₘ+ S₁-2mDₘ+6Dₘ

- 2S₂- Cₘ+mH-2Dₘ+3- Aₘ

= S₁+2Dₘ- 2S₂- Cₘ+mH+3- Aₘ

=2m²-5m+3+2(2m²-4m+5)

-2(m²-5m+6)-(2m²-3m+4)

+mH +3-2m²

= mH

对于最下一行来说，m=M=n/2（M指n阶幻方的最大格子数），又H＝n²+1，

∴ ∑₁= mH =MH

=n(1+n²)/2 （证毕）

2、最上行的和

设最下行的所有数字为N₁，N₂，…Nₙ ，则最上一行的和可以表示为

∑₂=（H- N₁）+（H- N₂）+…+（H- Nₙ ）

= nH-( N₁+ N₂+…+Nₙ )

=nH-MH

= nH-Hn/2

= Hn/2

=n(1+n²)/2 （证毕）

3、一般行的和

本幻方一般m行（指不含有4阶幻方的中间4行外的任何行）的编排特点，是斜轴外还有数字。由于被两斜轴分割的这些行，斜轴外两端的数字都是互补的，对应格子上的数字之和都是H。且斜轴内（含斜轴）的数字一共是2m个，两端各有（M-m）个数字，所以，根据上面第一点的结果（幻和为mH），有

∑₃= mH+（M-m）H

=MH

=n(1+n²)/2 （证毕）

4、中间的4行（4列同理）

对于含有中间4阶幻方的行和列来说，由于中间4阶幻方之和为2H，行或列的两端数字，都是互补的，所以，行列之和都可以表示为

∑₄=（M-2）H+2H

=MH

= n(1+n²)/2 (证毕)

5、最左列的证明

这列的所有数字之和，明显的是

∑₅=Aₘ+ (Aₘ-2)+ (Aₘ-4)+…

+[ Aₘ-2(m-2) ]+( H-Cₘ)+(H-Bₘ)+

+ [ (H-Bₘ)-2]+ [ (H-Bₘ)-4]+…

[(H-Bₘ)-2(m-2) ]+ Dₘ

=(m-1) Aₘ-[2+4+…+2(m-2) ]+ mH

-Cₘ-(m-1) Bₘ-[2+4+…+2(m-2) ]+ Dₘ

而根据等差和公式，有

S=2+4+…+2(m-2)=

=2(m-2)+ 2(m-2) (m-3)/2

= m²-3m+2，

∴ ∑₅=m Aₘ- Aₘ-2S+mH

-Cₘ-mBₘ+Bₘ+ Dₘ

=2m³-2m²-2(m²-3m+2)+ mH

-(2m²-3m+4)-m(2m²-2m+3)

+(2m²-2m+3)+(2m²-4m+5)

= mH

对于最左一列来说，m=M=n/2，

∴ ∑₅= mH =MH

=n(1+n²)/2 （证毕）

同理可以证明最右边的列。其他一般列，参照上述行的说明，不难证明，从略。

6、对角线的和

因为中间4阶幻方的幻和=2H，所以，对角线上数字之和是

∑₆= Aₘ+…+ A₄+ A₃+2H+ A₃＇+

A₄＇+ …+Aₘ＇＝

= (Aₘ+Aₘ＇)+…+ (A₄+A₄＇)+

(A₃+A₃＇)+ 2H

=(M-2)H+2H

=MH

＝n(1+n²)/2 （证毕）

由此得证，本偶阶幻方的每一行、每一列及对角线之和均相等，满足幻方的要求。

三、没有重复数的证明

根据本幻方的构造方法，当m=5，7，9时，在Ⅰ区域作了特别处理，避免了重复数，且不影响幻方的要求。

为什么这里会出现重复数，别的地方会不会呢？

由于Cₘ=2m²-3m+4，与取数范围

Dₘ﹤Nₘ﹤Bₘ-1

比较，由于

Dₘ=2m²-4m+5，

Bₘ-1=2m²-2m+3-1=2m²-2m+2，

显然， Dₘ﹤Cₘ﹤Bₘ-1

也就是说，Cₘ处在取数范围内，所以存在重复的可能；

而处在同一环的还有其他两处，其一，右下方是递增2的，即使最小的数，

Bₘ+2=2m²-2m+3+2﹥

Cₘ=2m²-3m+4，

所以无重复可能；

其二，另一处Aₘ、Aₘ-2、Aₘ-4、…Aₘ-2（m-2），是递减2的，但这里即使是最小的数，

即 Aₘ-2（m-2）=2m²-2m+4﹥

Cₘ=2m²-3m+4，

所以这里也不可能出现重复数。也就是说，本幻方除了取数范围内的数，有可能重复，其他地方无重复的可能。

阐明了重复的问题，另一个疑问就来了：这种递加、递减的构造方法，会不会掉了几个数？所以有必要展开讨论下。

在求幻和时，我们知道，本幻方的构造方法有这么一个特点：小数（N≤n/2）是由公式求得的，它的位置不因阶数的变化而变化；而大数（N＞n/2）是由互补关系求得的，它的位置随所取阶数的不同而不同。所以只要小数不出现重复，不掉数，大数必不会重复（不指误算的重复），不掉数。但为了使人信服，我们还是把小数和大数一起加以讨论。

参照图一，当m一定时，所有序号m相同的数字处在一个闭合的环上。现在我们来求一般情况下，m环上的所有数字。先看小数部分，小数部分一共分四处:

第一部分，是由Dₘ-2、Dₘ-1、Dₘ以及取数范围Dₘ﹤Nₘ﹤Bₘ-1所组成的小数，包含了上下两处的所有小数(含Cₘ)，且这些数字是“连续”的（我们把公差为1的一系列数，称为连续）；

第二部分，左上半列，由Aₘ、Aₘ-2、Aₘ-4、…Aₘ-2（m-2），一共（m-1）个数；

第三部分，右下半列，由Bₘ、Bₘ+2、Bₘ+4、…Bₘ+2（m-2），一共（m-1）个数。

考虑到通项公式

Aₘ=2m²

Bₘ=2m²-2m+3

Dₘ=2m²-4m+5，有

第一部分，Dₘ-2= 2m²-4m+5-2

= 2m²-4m+3

Bₘ-1=2m²-2m+3-1=2m²-2m+2，

由于第一部分数字是连续的，我们用如下形式表示

2m²-4m+3→2m²-2m+2 （1）

（在本证明中，我们用符号a→b表示由a到b的一组递增1或递减1的数列，用符号c→→d表示由c到d的一组递增2或递减2的数列）

第二部分，Aₘ=2m²，

Aₘ-2（m-2）=2m²-2m+4，

即

2m² →→2m²-2m+4 （表示递减2）

变为递增，有

2m²-2m+4 →→2m² (表示递加2）

即 2(m²-m+2) →→2m² (2)

明显看出，这是一个公差为2的偶数数列；

第三部分， Bₘ=2m²-2m+3

Bₘ+2（m-2）

=2m²-2m+3+2m-4=2m²-1

即

2m²-2m+3→→2m²-1 （表示递加2）

即 2(m²-m+1) +1→→2m² -1 (3)

这是一个公差为2的奇数数列。

比较（2）（3）式子，两式项数一样，都是（m-1）个数，且两式左右端恰好相差1，所以两式可以合并为一个连续数列，即

2m²-2m+3→2m² （4）

2m²-4m+3→2m²-2m+2 （1）

比较（1）（4）式，（4）式的左端比（1）式的右端恰好大1，所以这两条式子可以合并为

2m²-4m+3→2m² （5）

也就是说，处在m环上的小数数字，恰好组成一个连续数列。

下面讨论大数——

根据本幻方的构造特点，大数都是由与小数互补的关系求得的。尽管幻方左右两区域有递增递减2的简洁关系(这也正是本构造的价值所在)，但这并不能否定大数都是由互补关系求得的事实。所以，既然小数是连续的，大数必然也是连续的。用上述讨论小数的办法，或直接利用小数的结果，我们都得到了下式

H-2m²→H-(2m²-4m+3) （6）

比较（5）（6）两式，由于

（H-2m²）- 2m²= H-4m²=(n²+1)- 4m²

对于给定的n阶幻方，m的最大数为M，而M=n/2，代入上面的结果，有

(n²+1)- 4m²=(n²+1)-4 (n/2)²=1＞0,

也就是说，大数数列的最小数，比小数数列的最大数还要大，所以这两组数列没有重复数。

结论一 在本幻方的m环上，没有重复数。

现在来看m+1环的情况。将m+1代入（5）式，我们发现新数列与原数列恰好是连续的。用下列图示的办法，更能直观反映这种关系:

设m环的小数数列的两端数字为a、b，大数数列两端的数字为c、d，而a＇、c＇等，表示m+1时的新数列两端数字（见下）

小数数列

a → b， a＇→ b＇ …

m m+1 …

大数数列

… c＇→ d＇ c → d，

… m+1 m

讨论发现，当格子序号取m、m+1时，恒有

a＇= b + 1， c= d＇+ 1

对照（5）式 2m²-4m+3→2m²

小数满足如下关系，即

2(m+1)²-4(m+1)+3=2m²+1 （7）

下面用数学归纳法来确认上面的结论了:

当m=3时（本幻方序号m=1,2是中心4阶幻方），（7）式

左边= 19，右边=19 ，说明（7）式成立；

假设当m=k（k≥3）时，（7）式也成立，即

2(k+1)²-4(k+1)+3=2k²+1

当m=k+1时，有

左边= 2(m+1)²-4(m+1)+3

= 2(k+1+1)²-4(k+1+1)+3

=2(k+1)²+4(k+1)+2-4(k+1)-4+3

=2(k+1)²+1

右边=2m²+1=2(k+1)²+1

即 左边=右边

因此，对于任意m≥3的自然数m，等式（7）均成立。用数学归纳法，同样可求得大数数列也成立。由此，我们得到——

结论二 任意互为相邻的正方环上的所有数字，都可以组成两个连续的递增数列，并且大递增数列的最小数，总是大于小递增数列的最大数。

组成幻方的每个正方环都是互为相邻的，整个幻方就是由这些互为相邻的正方环上的数字组成的。由此，我们得到总结论——

本幻方序号m≥3的正方环上的所有数字，恰好组成两个连续的递增数列，并且大递增数列的最小数总是大于小递增数列的最大数，当然没有重复数。

下面我们来求解这两个数列，看看有没有掉了几个数？

对于给定的n偶阶幻方来说，它的最大格子序号设为M，容易看出

M=n/2 → n=2M

将M代入（5）式2m²-4m+3→2m² ，有

n²/2-2n+3→n²/2 (8)

将M代入（6）式

H-2m²→H-(2m²-4m+3) ，

考虑到H= n²+1，即得

n²+1-n²/2 →(n²+1)-(n²/2-2n+3)

即

n²/2+1→n²/2+2n-2 (9)

(8)式数列，表示的正是任意n阶幻方最大序号M正方环上的小数数字，(9)式数列，表示的正是任意n阶幻方最大序号M正方环上的大数数字。

如果将M-1代入上述两式，则得到的是M-1环上的两个数列；如果对于小数数列，左端代入M-1，右端代入M，则数列表示的，是从M-1环到M环的两环小数数列，大数数列同理。就是说，一般地

2m²-4m+3→n²/2

n²/2+1→(n²+1)-(2m²-4m+3)

两式表示的就是从m环到M环的所有大、小两数数列。

当m=3时，有

9→n²/2 (10)

n²/2+1→n²-8 (11)

考虑到中间4阶幻方的2对数列

1→8 ， n²-7→n²

结合（10）（11）式子，有

1→8 ， 9→n²/2 ，

n²/2+1→n²-8 ， n²-7→n²

这四个数列，明显是两两连续的，即

1→n²

也就是说，上述两个递增数列，连上中间4阶幻方的两对数列，恰好是一个1至n²的自然数数列。

综上所述，根据本方法排列的幻方上的所有数字，恰好是1至n²的自然数，没有重复数，也没有掉数。

再给大家配上一个大佬的证明方法https://zhuanlan.zhihu.com/p/616471584

然后给大家看一下本蒟蒻写的洛谷B3940 [GESP样题 四级] 填幻方的代码

#include<iostream>
#include<fstream>
#include <vector>
#include <iomanip>
#include <bits/stdc++.h>
#include <math.h>
#include <algorithm>
#include <cstring>
using namespace std;
int n,a[25][25];
int main(){
	cin>>n;
	int x=0,y=n/2;
	a[x][y]=1;
	for(int cnt=2;cnt<=n*n;cnt++){
		int tx=(x+n-1)%n;
		int ty=(y+1)%n;
		if(a[tx][ty]==0){
			a[tx][ty]=cnt;
		}else{
			tx=(x+1)%n;
			ty=y;
			a[tx][y]=cnt;
		}
		x=tx;
		y=ty;
	}
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
	return 0;
}

可以完美的解决幻方问题

蓝后就是大家全文背诵并默写了

最后配上AC记录https://www.luogu.com.cn/record/159520201

OK，就瞎扯到这里吧