邻接多重表
上一节总结了有向图的另外一种链式存储结构—十字链表，该节继续总结无向图的另一种链式存储结构。
基本概念
邻接表虽然已经能够很好地表示无向图了，但是无向图访问或者删除一条边(Vi,Vj)时需要同时访问两个链表i和j并分别找到对应的边结点，这给针对图的边的操作（标记或删除）带来不便利。邻接多重表因此而演变过来的。
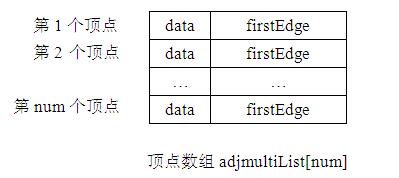
邻接多重表中，无向图中的每一个顶点分配一个顶点结点，所有顶点结点构成一个顶点数组adjmultiList[num]。另外每条边也分配一个边结点。
顶点结构如下所示：
其中data用来记录顶点的信息，firstEdge用来表示依附于该顶点的第一条边。
顶点数组如下所示：
边结点结构如下所示：
其中mark表示标志位，用于标记该边是否已经被访问过；iVex和jVex表示该边的两个顶点在顶点数组adjmultiList[num]中的位置；iLink和jLink分别表示指向依附于顶点iVex和jVex下一条边的指针。
从上面的顶点和边的结构来看，邻接多重表和邻接表的主要区别在于：邻接多重表中的边结点同时被链入对应边顶点的链表内（2条）；邻接表中的边用两个表结点表示。另外，邻接多重表中的边结点就表示一条边，比较容易理解。
举个例子。某无向图如下图所示：
当采用邻接表表示该无向图时，其邻接表入下图所示：
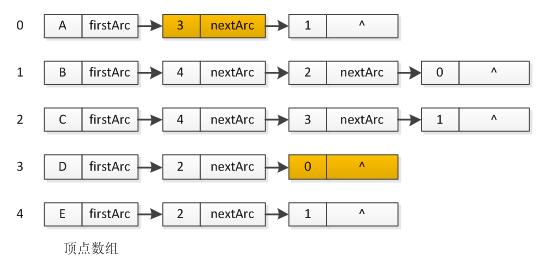
如上图所示，图中黄色标记的结点表示A-D之间的边，在邻接表中一条边需要两个结点表示。因此如果对于边的操作（标记或者删除）则需要访问两条链表。
当采用邻接多重表表示该无向图时，其邻接多重表入下图所示：
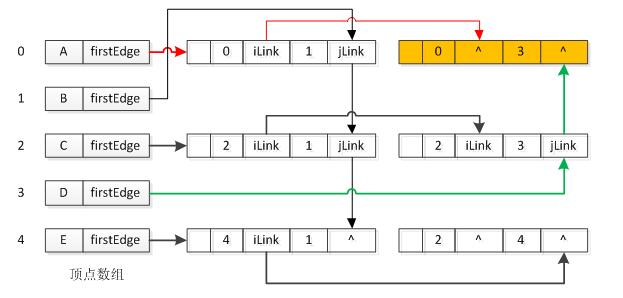
如上图所示，结点A-D 之间的边，在邻接多重表中只需要一个边结点既可以表示。另外，在该结构中，每个边结点被链入了两个不同的链表。其中A-D之间的边被链入了红色和绿色标记的链表中。如果需要访问一条边，则可以从该边的两个顶点结点中的任何一个出发，遍历依附于该顶点的边构成的链表即可。如果需要删除一条边，则只需要删除一个边结点，但是需要修改这条边依附的两个顶点所对应的链表。另外，需要注意的是，在无向图中，边结点中的iVex和jVex链域与该边所依附的顶点无关，即iVex=0，jVex=3和iVex=3，jVex=0这都表示同一条边A-D，因此这给链表的指针修改带来一定的麻烦。
基本操作
1、建立无向图的邻接多重表
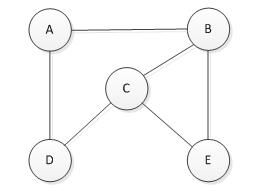
输入ABCDE五个顶点V={A,B,C,D,E}，然后输入边E={(A,B),(B,C),(B,E),(C,D),(C,E),(D,A)}，建立如下无向图：
代码如下：
Status createAMLGraph(AMLGraph &G, int vexNum){
G.vexNum = vexNum;
G.edgeNum = 0;
for(int i = 0; i< G.vexNum; i++){
cin>>G.adjmultiList[i].data;
G.adjmultiList[i].firstEdge = NULL;
}
cout<<"Try to input arcs info"<<endl;
while(1){
char SWITCH;
cout<<"are you going to add a edge into AMLGraph?(y?n)"<<endl;
cin>>SWITCH;
if(SWITCH == 'y'){
cout<<"please input two nodes of "<<G.edgeNum+1<<"-th arc"<<endl;
vertexNode node1, node2;
cin>>node1.data>>node2.data;
insertEdge(G, node1, node2);
G.edgeNum++;
}
else
break;
}
return 1;
}2、打印无向图的邻接多重表
代码如下：
Status printAMLGraph(AMLGraph &G){
for(int i = 0; i<G.vexNum; i++){
cout<<i<<" "<<G.adjmultiList[i].data;
edgeNode *edge = G.adjmultiList[i].firstEdge;
while(edge){
cout<<"-->|"<<edge->iVex<<"|"<<edge->jVex<<"|";
if(edge->iVex == i){
edge = edge->iLink;
}
else{
edge = edge->jLink;
}
}
cout<<"-->NULL"<<endl;
}
return 1;
}3、向无向图中添加顶点
向无向图中添加结点F。
代码如下：
Status insertNode(AMLGraph &G, vertexNode node){
G.adjmultiList[G.vexNum].data = node.data;
G.adjmultiList[G.vexNum].firstEdge = NULL;
G.vexNum++;
return 1;
}4、向无向图中添加边
向无向图中添加边A-C。
代码如下：
void insertEdgeAction(AMLGraph &G, int index1, int index2){
edgeNode *p, *q;
edgeNode *edge = new edgeNode[1];
edge->iVex = index1;
edge->jVex = index2;
p = G.adjmultiList[index1].firstEdge;//相当于链表的插入
if(!p){
G.adjmultiList[index1].firstEdge = edge;
edge->iLink = NULL;
}
else{
G.adjmultiList[index1].firstEdge = edge;
edge->iLink = p;
}
q = G.adjmultiList[index2].firstEdge;//相当于链表的插入
if(!q){
G.adjmultiList[index2].firstEdge = edge;
edge->jLink = NULL;
}
else{
G.adjmultiList[index2].firstEdge = edge;
edge->jLink = q;
}
}
Status insertEdge(AMLGraph &G, vertexNode node1, vertexNode node2){
int index1 = locateNode(G, node1);//i和j表示AdjList[MAX_VERTEX_NUM]中的位置
int index2 = locateNode(G, node2);
if(index1<0 || index2<0) exit(-1);
insertEdgeAction(G, index1, index2);
return 1;
}5、删除无向图中的边
删除无线图中的边B-C。
代码如下：
Status deleteEdgeAction(AMLGraph &G, int index1, int index2){
edgeNode *curEdge = G.adjmultiList[index1].firstEdge;
edgeNode *preEdge = curEdge;
int count = 0;
if(!curEdge) return 1;
else{
while(curEdge){
count++;
if((curEdge->iVex == index1&&curEdge->jVex == index2)||(curEdge->iVex == index2&&curEdge->jVex == index1)){
break;
}
preEdge = curEdge;
if(curEdge->iVex ==index1)
curEdge = curEdge->iLink;
else
curEdge = curEdge->jLink;
}
}
if(!curEdge)
return 1;
else if(count<=1){
if(preEdge->iVex == index1)
G.adjmultiList[index1].firstEdge = preEdge->iLink;
else
G.adjmultiList[index1].firstEdge = preEdge->jLink;
}
else{
if(preEdge->iVex == index1){
if (curEdge->iVex == index1)
preEdge->iLink = curEdge->iLink;
else
preEdge->iLink = curEdge->jLink;
}
else{
if (curEdge->iVex == index1)
preEdge->jLink = curEdge->iLink;
else
preEdge->jLink = curEdge->jLink;
}
}
return 1;
}
Status deleteEdge(AMLGraph &G, vertexNode node1, vertexNode node2){
int index1 = locateNode(G, node1);
int index2 = locateNode(G, node2);
deleteEdgeAction(G, index1, index2);
deleteEdgeAction(G, index2, index1);
return 1;
}6、删除无向图中的顶点
删除结点C。
代码如下：
Status deleteNode(AMLGraph &G, vertexNode node){
//删除结点时，结点不真实删除而只是删除结点相关的边以及赋值该结点的data为特殊值‘0’
int index = locateNode(G, node);
for(int i = 0; i<G.vexNum; i++){
if(i == index) continue;
else{
deleteEdge(G, G.adjmultiList[index], G.adjmultiList[i]);
}
}
G.adjmultiList[index].firstEdge = NULL;
G.adjmultiList[index].data = '0';
return 1;
}7、全部代码：
// 邻接多重表.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
#define MAX_VERTEX_NUM 20
typedef int infoType;
typedef char vertexType;
typedef int Status;
typedef struct edgeNode{
int iVex, jVex;
struct edgeNode *iLink, *jLink;
infoType *info;
}edgeNode;
typedef struct vertexNode{
vertexType data;
edgeNode *firstEdge;
}vertexNode;
typedef struct{
vertexNode adjmultiList[MAX_VERTEX_NUM];
int vexNum, edgeNum;
}AMLGraph;
int locateNode(AMLGraph &G, vertexNode node){
for(int i=0; i<G.vexNum;i++){
if(node.data == G.adjmultiList[i].data)
return i;
}
return -1;
}
Status insertEdge(AMLGraph &G, vertexNode node1, vertexNode node2);
Status createAMLGraph(AMLGraph &G, int vexNum){
G.vexNum = vexNum;
G.edgeNum = 0;
for(int i = 0; i< G.vexNum; i++){
cin>>G.adjmultiList[i].data;
G.adjmultiList[i].firstEdge = NULL;
}
cout<<"Try to input arcs info"<<endl;
while(1){
char SWITCH;
cout<<"are you going to add a edge into AMLGraph?(y?n)"<<endl;
cin>>SWITCH;
if(SWITCH == 'y'){
cout<<"please input two nodes of "<<G.edgeNum+1<<"-th arc"<<endl;
vertexNode node1, node2;
cin>>node1.data>>node2.data;
insertEdge(G, node1, node2);
G.edgeNum++;
}
else
break;
}
return 1;
}
void insertEdgeAction(AMLGraph &G, int index1, int index2){
edgeNode *p, *q;
edgeNode *edge = new edgeNode[1];
edge->iVex = index1;
edge->jVex = index2;
p = G.adjmultiList[index1].firstEdge;//相当于链表的插入
if(!p){
G.adjmultiList[index1].firstEdge = edge;
edge->iLink = NULL;
}
else{
G.adjmultiList[index1].firstEdge = edge;
edge->iLink = p;
}
q = G.adjmultiList[index2].firstEdge;//相当于链表的插入
if(!q){
G.adjmultiList[index2].firstEdge = edge;
edge->jLink = NULL;
}
else{
G.adjmultiList[index2].firstEdge = edge;
edge->jLink = q;
}
}
Status insertEdge(AMLGraph &G, vertexNode node1, vertexNode node2){
int index1 = locateNode(G, node1);//i和j表示AdjList[MAX_VERTEX_NUM]中的位置
int index2 = locateNode(G, node2);
if(index1<0 || index2<0) exit(-1);
insertEdgeAction(G, index1, index2);
return 1;
}
Status printAMLGraph(AMLGraph &G){
for(int i = 0; i<G.vexNum; i++){
cout<<i<<" "<<G.adjmultiList[i].data;
edgeNode *edge = G.adjmultiList[i].firstEdge;
while(edge){
cout<<"-->|"<<edge->iVex<<"|"<<edge->jVex<<"|";
if(edge->iVex == i){
edge = edge->iLink;
}
else{
edge = edge->jLink;
}
}
cout<<"-->NULL"<<endl;
}
return 1;
}
Status insertNode(AMLGraph &G, vertexNode node){
G.adjmultiList[G.vexNum].data = node.data;
G.adjmultiList[G.vexNum].firstEdge = NULL;
G.vexNum++;
return 1;
}
Status deleteEdgeAction(AMLGraph &G, int index1, int index2){
edgeNode *curEdge = G.adjmultiList[index1].firstEdge;
edgeNode *preEdge = curEdge;
int count = 0;
if(!curEdge) return 1;
else{
while(curEdge){
count++;
if((curEdge->iVex == index1&&curEdge->jVex == index2)||(curEdge->iVex == index2&&curEdge->jVex == index1)){
break;
}
preEdge = curEdge;
if(curEdge->iVex ==index1)
curEdge = curEdge->iLink;
else
curEdge = curEdge->jLink;
}
}
if(!curEdge)
return 1;
else if(count<=1){
if(preEdge->iVex == index1)
G.adjmultiList[index1].firstEdge = preEdge->iLink;
else
G.adjmultiList[index1].firstEdge = preEdge->jLink;
}
else{
if(preEdge->iVex == index1){
if (curEdge->iVex == index1)
preEdge->iLink = curEdge->iLink;
else
preEdge->iLink = curEdge->jLink;
}
else{
if (curEdge->iVex == index1)
preEdge->jLink = curEdge->iLink;
else
preEdge->jLink = curEdge->jLink;
}
}
return 1;
}
Status deleteEdge(AMLGraph &G, vertexNode node1, vertexNode node2){
int index1 = locateNode(G, node1);
int index2 = locateNode(G, node2);
deleteEdgeAction(G, index1, index2);
deleteEdgeAction(G, index2, index1);
return 1;
}
Status deleteNode(AMLGraph &G, vertexNode node){
//删除结点时，结点不真实删除而只是删除结点相关的边以及赋值该结点的data为特殊值‘0’
int index = locateNode(G, node);
for(int i = 0; i<G.vexNum; i++){
if(i == index) continue;
else{
deleteEdge(G, G.adjmultiList[index], G.adjmultiList[i]);
}
}
G.adjmultiList[index].firstEdge = NULL;
G.adjmultiList[index].data = '0';
return 1;
}
int _tmain(int argc, _TCHAR* argv[])
{
int vexNum = 5;
AMLGraph G;
cout<<"Try to create a adjacence multilist of a graph ..."<<endl;
createAMLGraph(G, vexNum);
printAMLGraph(G);
cout<<"Try to insert a node into the graph..."<<endl;
vertexNode node;
cout<<" please input the data of the node to insert:"<<endl;
cin>>node.data;
insertNode(G, node);
printAMLGraph(G);
cout<<"Try to insert a edge into the graph..."<<endl;
vertexNode node1, node2;
cout<<" please choose two node:"<<endl;
cin>>node1.data>>node2.data;
insertEdge(G, node1, node2);
printAMLGraph(G);
cout<<"Try to delete the edge between two nodes..."<<endl;
vertexNode node3, node4;
cout<<" please choose a edge with specifing two nodes:"<<endl;
cin>>node3.data>>node4.data;
deleteEdge(G, node3, node4);
printAMLGraph(G);
cout<<"Try to delete a node of the graph..."<<endl;
vertexNode node5;
cout<<" please choose a node:"<<endl;
cin>>node5.data;
deleteNode(G, node5);
printAMLGraph(G);
system("pause");
return 0;
}
1709
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
