CF701B Cells Not Under Attack 题解

博客园同步

原题链接

简要题意：

在棋盘上放若干个车，车可以攻击到同行同列的棋子。求放完每个车后，不被攻击的棋子个数。

洛谷 题解 里说要用 $\text{set}$ 维护，但本人觉得，可以做到线性解决问题！

其实，你可能觉得，$O(n\times m)$ 模拟一下就行啊！

模拟方法大致是：

一开始答案为 $n^2$，每放一个车，横竖扫一遍，如果没有被标记过（标记可以用二维数组，也可以用 $\text{map}$ 嵌套 $\text{pair}$），那么就答案减少 $1$. 每次输出。

时间复杂度：$O(n\times m)$. 空间复杂度：$O(n^2)$.

如果你改用 $\text{map}$ 维护标记，搞定内存问题，那么：

时间复杂度：$O(n\times m\log m)$. 空间复杂度：$O(n)$.

无论怎样，都无法 $n\le 10^5$，$m\le \min (10^5,n^2)$ 这样的强大数据。

所以要寻找本质。

你会发现，最终被攻击的棋子一定是若干整行，若干整列。

那么，如果平移这些行列，会不会对答案产生影响？

不会。

所以，如果车有 $x$ 个不同行，$y$ 个不同列，那么被攻击的棋子就可以通过平移（小学思路）成为一个 这样的形状：

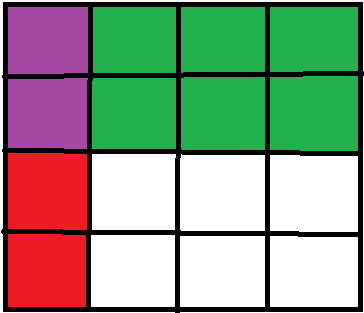
（$x=2$，$y=1$ 的例子，重复部分用紫色标出）

此时没被攻击的就是 $(n-x)\times (n-y)$ 个，这也很好理解吧？

所以维护行列的不同，然后解决本题。

时间复杂度：$O(m)$.

空间复杂度：$O(n)$.

实际得分：$100pts$.

看到了吧，比 set 快多了（不过本质是一样的）

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

inline ll read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
	ll x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

const ll N=1e5+1;
ll a[N],b[N],n,m;

int main(){
	cin>>n>>m;
	ll num=0,ant=0;
	while(m--) {
		ll x=read(),y=read();
		if(!a[x]) a[x]=1,num++;
		if(!b[y]) b[y]=1,ant++;
		printf("%lld ",(n-num)*(n-ant));
	}
	return 0;
}